Equations différentielles
- par gabriel
- dans Equations inéquations, Mathématiques
- sur 15 mai 2021

Définition
Une équation différentielle est une équation dont l’inconnue est une fonction; Cette équation est constituée généralement de la fonction avec une ou plusieurs de ses dérivées (dérivée première, dérivée seconde). Résoudre une équation différentielle consiste à trouver la fonction inconnue. Il existe plusieurs sortes d’équations différentielles que nous découvrirons au fil de cet article.
Il existe aussi plusieurs notations dont les principales sont représentées ci-contre avec leur signification.
![]()
Il s’agit de trouver la fonction y(x) dont la variable est x et dont la dérivée moins deux fois cette fonction soit égale à 2x+1.
On peut écrire cette équation avec la notation traditionnelle :![]()
Mais habituellement on utilise la première notation.
On trouve parfois une notation différentielle.
Rappel un très petit accroissement ou accroissement infinitésimal de la fonction y se note dy Il en est de meêm pour un accroissement infinitésimal de la variable x noté dx La dérivée d’une fonction est la limite de l’accroissement des y ou f(x) divisé par l’accroissement des x quand l’accroissement des x tend vers 0 c’est à dire quand cet accroissement est infiniment petit. ![]()
On peut donc écrire notre équation :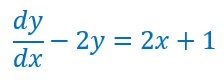
Equation linéaire sans second membre à coefficiants réels
C’est une équation du genre :![]()
ou en écriture simplifiée :![]()
Ou encore ![]()
Il s’agit de trouver une fonction dont la dérivée lui est égale à -a fois.
La seule fonction qui est égale à sa dérivée est la fonction exponentielle.
En effet :![]()
Il existe une infinité de fonctions égales à leur dérivée. Pour k, un nombre quelconque de l’ensemble des réels, ![]()
De plus la dérivée doit être égale à -a fois la fonction.
Cette fonction sera de la forme :![]()
car sa dérivée ![]()
est bien égale à m fois la fonction.
Introduisons cette fonction dans notre équation différentielle :![]()
En factorisant, 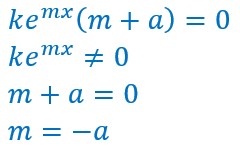
Ainsi la fonction recherchée sera-t-elle égale à ![]()
Vérifions en reportant cette solution dans l’équation différentielle de départ : ![]()
C’est bien juste.
Ainsi il existe une infinité de fonctions solutions de notre équation différentielle. Cette infinité se trouve en faisant varier k de -∞ à +∞.
Pour résoudre de telles équations, on peut soit effectuer les calculs ci-dessus, soit utiliser l’une des formules ci-dessous : ![]()
![]()
Voyons un cas concret :![]()
Il s’agit de trouver les fonctions telles que pour chacune d’elles 4 fois sa dérivée plus 3 fois la fonction soit égal à 0.
On peut écrire cette équation différentielle en divisant par le coefficiant de la dérivée 4 : Ou encore :
Ou encore : 
Il faut donc trouver les fonctions dont chacune d’elle est égale aux moins trois quarts de sa dérivée.
Une fonction qui est égale à sa dérivée est la fonction exponentielle :![]()
En multipliant les deux membres par k, on trouve une infinité de fonctions égales à leur dérivée :![]()
Si on considère la fonction ![]()
sa dérivée sera ![]()
Cette dérivée est égale à mk fois la fonction.
On remplace dans l’équation différentielle initiale :![]()
![]()
On factorise :![]()
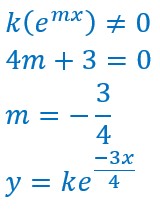
Tel est l’ensemble des fonctions. Il en existe une infinité puisque k peut prendre toutes les valeurs dans l’ensemble des réels.
On peut représenter graphiquement quelques unes de ces fonctions :

Equation linéaire sans second membre
Nous venons d’étudier les équations différentielles à coefficient a constant. Mais ce coefficient peut-être une fonction a(x).
Etudions les équations différentielles de la forme : 
On peut écrire :![]()
Il s’agit de trouver une fonction f(x) dont la dérivée f'(x) est égale au produit d’une fonction a(x) par la fonction recherchée. Soit une fonction g(x) au coefficient k près :![]()
La dérivée de cette fonction est :![]()
En effet, d’après les composition de fonction, la dérivée d’une fonction composée est égale au produit des dérivées. Dans ce cas la dérivée de eg(x) est égale à la dérivée de g(x) multiplié par la dérivée de eg(x).
Introduisons cette dérivée dans l’équation différentielle du début avec le coefficient k : ![]()
![]()
Nous pouvons écrire :![]()
Factorisons :![]()
Nous savons qu’une fonction exponentielle n’est jamais égale à 0.![]()
Donc 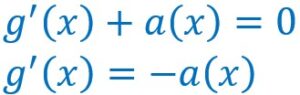
Soit en intégrant les deux membres, c’est-à-dire en prenant les primitives des deux membres :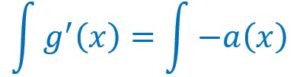
![]()
A(x) étant la primitive de a(x).
La fonction recherchée est donc :![]()
Soit a(x) une fonction continue à coefficients réels définie sur un intervalle I. Les solutions de l’équation différentielle y’+a(x)y=0 sont toutes les fonctions y=ke-A(x) , A(x) étant une primitive de a(x).

![]()
Soit l’équation différentielle :![]()
Nous voyons qu’elle est de la forme a(x)y’-b(x)y=0.
Pour la rendre de la forme étudiée ci-contre, il suffit de diviser ses deux membres par (x²+1) qui est toujours différent de 0 (somme d’un carré positif plus 1).
Chaque fois que nous aurons une équation différentielle de ce genre, on divisera par la fonction coefficientant y’ en tenant compte des restrictions éventuelles, de manière à n’avoir que y’ seul.

la fonction y, solution de l’équation sera forcément une fonction exponentielle au coefficient k près. ![]()
Mais nous savons que d’après les compositions de fonctions, la dérivée d’une fonction composée est :![]()
en tenant compte du coefficient réel k, on peut écrire en reportant dans l’équation initiale : 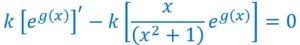
![]()
On factorise :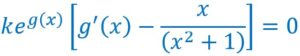
![]()


Soit en intégrant les deux membres (le signe de l’intégration devant une fonction revient à trouver une primitive de cette fonction. 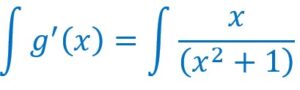
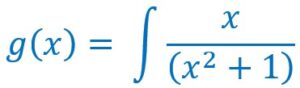
Pour calculer cette primitive, il faudrait avoir au numérateur, la dérivée 2x du dénominateur.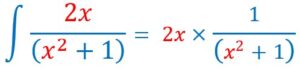
Donc :
On en déduit la fonction primitive : 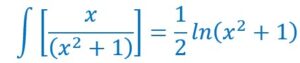
Voir les formules sur les primitives
Voir les calculs sur les exposants de quatrième, puis le résultat de deux fonctions réciproques :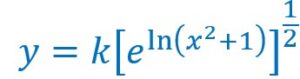
, ![]()
![]()
Représentation graphique :
Equations différentielles avec second membre (non homogènes)
Le second membre est une constante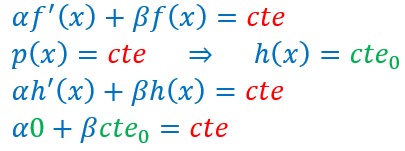
Le second membre est une fonction affine 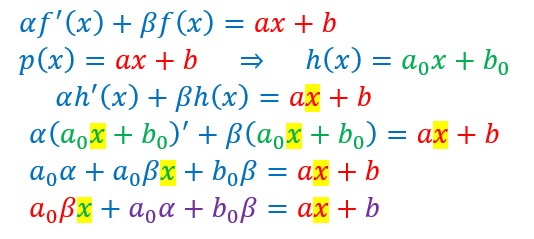
Pour trouver a0 et b0, il suffit d’identifier les deux membres.
Le second membre est une fonction du second degré
Pour trouver a0,b0 et c0, il suffit d’identifier les deux membres.
Le second membre est une fonction exponentielle.

Soit αf'(x)+βf(x)=p(x) ou αy’+βy=p(x) une équation différentielle.
p(x) est une fonction pouvant prendre plusieurs formes ( polynôme, fonction trigonométrique, fonction exponentielle, fonction constante….). Selon la forme de p(x) on en déduira la forme d’une des fonction solution particulière y ou f(x). Soit h(x) cette fonction solution particulière.
Si p(x)=cte on pourra en déduire que l’une des fonctions solution sera une fonction constante ( en effet la dérivée d’une fonction constante est nulle donc α fois une dérivée nulle plus β fois une fonction constante nous donnera bien une fonction constante.
Si p(x) est un polynôme du premier degré, on en déduira forcément que la fonction cherchée sera un polynôme du premier degré de la forme ax+b (en effet α fois une dérivée constante plus β fois une fonction du premier degré est bien égale à une fonction du premier degré). Il nous faudra déterminer les coefficients de ce polynôme fonction solution particulière.
On continue ainsi
Si p(x) est du second degré ax²+bx+c, la fonction solution particulière sera forcément un polynôme du second degré dont il nous faudra déterminer les coefficients de x .
Si p(x) est une fonction trigonométrique en sinus ou cosinus ou les deux, la fonction solution sera obligatoirement de la forme asin(x)+bcos(x).
Si p(x) est une fonction exponentielle, la fonction solution sera forcément de la forme aex+b
Etc….etc….
Une fois qu’on connaît cette solution particulière il ne nous reste plus qu’à en calculer la dérivée puis de reporter ces valeurs dans le premier membre et d’identifier avec le second membre pour trouver les valeurs des coefficients.
Ainsi on obtient une fonction particulière h(x) qui vérifie l’équation différentielle donnée.
Ainsi on obtient une fonction particulière qui vérifie l’équation différentielle données![]()
Soit f(x) une solution générale de cette équation forcément elle vérifiera l’équation différentielle donnée.![]()
En résumé, on a donc une solution particulière et une solution générale qui vérifient toutes deux l’équation différentielle :
Les deux premiers membres sont tous les deux égaux à p(x) . Aussi ils sont égaux entre eux :![]()
![]()
Si on désigne par![]()
![]()
Miracle ! on obtient une équation différentielle sans second membre qu’on sait résoudre . Sa solution est de la forme![]()
Soit :![]()

On vient de trouver la fonction générale qui vérifie l’équation différentielle: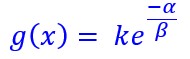
Il faut lui ajouter la fonction particulière trouvée précédemment. 
Soit l’équation différentielle :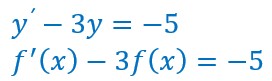
écrite sous deux formes différentes, pour la résoudre nous utiliserons la deuxième forme.
Le second membre de cette équation est une constante C . Nous avons vu dans la chapitre précédent qu’une solution particulière de cette équation était une constante :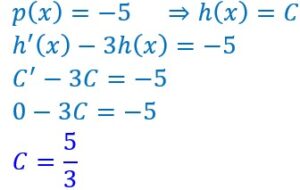
Nous avons remplacé cette constante C dans l’équation pour en calculer sa valeur.
Ainsi nous avons deux équations :
qui ont même second membre. Donc leur premier membre sont égaux.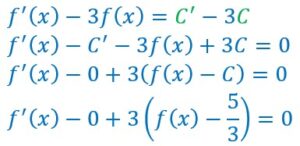
Soit :
donc :
Remplaçons dans l’équation :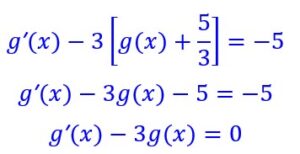
Nous obtenons une équation différentielle sans second membre. Nous savons la résoudre.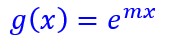
Calculons m en reportant dans l’équation :
Ainsi on a la solution générale de cette équation différentielle :![]()
Il nous reste à lui ajouter la solution particulière :
On trouve donc une infinité de solutions suivant les valeurs de k.
Ci contre on représente quelques unes de ces solutions pour k compris entre -5 et 5 avec un incrément de 0,1.
Faire glisser le curseur k pour que s’affiche une solution.
Ci-dessous toutes les solutions précédentes sont affichées.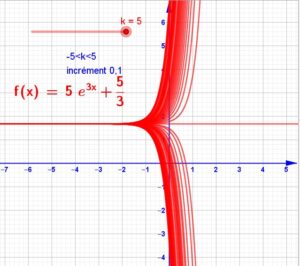
Soit l’équation différentielle :![]()
D’après le second membre qui est une fonction affine nous pouvons envisager qu’une fonction affine de la forme![]()
puisse être une des solutions de notre équation.
Si c’est le cas on aura y’=a et en remplaçant dans notre équation d’origine, on peut écrire :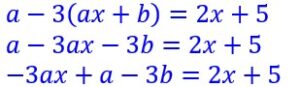
Par identification des deux membres on en déduit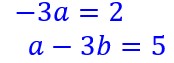

Ainsi la fonction![]()
est-elle UNE solution de l’équation différentielle Mais il y en a d’autres
Soit la fonction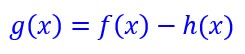
![]()
Cette fonction vérifiera notre équation différentielle si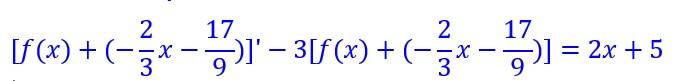
soit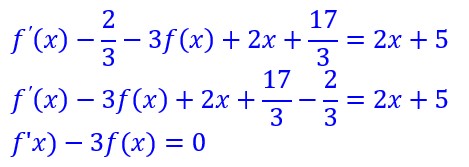
Or l’ensemble des solutions de cette équation sans second membre est une droite vectorielle don un vecteur directeur est de la forme![]()
Dans ce cas on aura
Le vecteur directeur de la droite vectorielle des solutions de cette équation sera donc![]()
L’ensemble des solutions sera l’ensemble des vecteurs colinéaires soit
Or puisque
Alors l’ensemble des solutions sera
On vérifiera aisément la validité de cette solution
Nous avons vu ci-contre que les solutions générales de l’équation différentielle :![]()
était :
Suivant les valeurs de k qui appartient à l’ensemble des réels, nous avons une infinité de solutions.
Ci-dessous nous faisons varier k de -10 à +10. Pour cacune des valeurs de k nous obtenons une fonction particulière dont nous pouvons visualiser la représentation graphique.
Ci-dessous la trace de chacune des fonctions selon les valeurs de k est conservée.
Nous avons donc toutes les solutions pour k compris entre -10 et +10.
Problème du bac
1) Résoudre l’équation différentielle![]()
dont l’inconnue est une fonction définie et dérivable
sur![]() .
.
2) On considère l’équation différentielle![]()
a. Déterminer deux réels m et p tels que la fonction f définie sur R par![]()
soit une solution de (E’)
b. Soit g une fonction définie et dérivable sur R. Montrer que g est solution de (E’) si et seulement si
g-f est solution de (E) .
Résoudre l’équation (E’).