Exercices d’hier et d’aujourd’hui
- par gabriel
- dans Articles nouveaux, Exercices, Mathématiques
- sur 20 mars 2024
Ajoutez votre titre ici
Classes élémentaires 1960
Un marchant de fruits et légumes a acheté l’ensemble de sa marchandise 2 euros le kilo.
Il vend les tomates 5 euros le kilo. Celles-ci représentent le tiers de la marchandise.
Le quart de sa marchandise sont des pommes vendues 4 euros le kilo.
Le reste est vendu au prix coûtant.
La totalité de sa marchandise lui permet de réaliser un bénéfice de 198 euros.
Quelle quantité de fruits et légumes en kilo a-t-il acheté au départ ?
Il s’agit de résoudre ce problème sans l’aide de l’algèbre qui ne sera étudié que dans l’enseignement secondaire.
Pour cela on fait une supposition sur la solution, une supposition qui sera forcément fausse.
Imaginons que le marchand achète 12 kg de marchandise et calculons son bénéfice
Sa dépense ou le pris d’achat serait : 2 x 12 = 24 €.
La vente des tomates, donc le tiers de la marchandise soit 12 : 3 = 4 kg lui rapporterait : 5 x 4 = 20 €
La vente des pommes qui représentent le quart de sa marchandise soit 12 : 4 = 3 kg lui rapporterait: 4 x 3 = 12 €
Le reste représentant 12 kg – 4 kg – 3 kg = 5 kg lui rapporterait : 2 x 5 = 10 € puisque le prix coûtant est le prix d’achat soit 2 €.
Au total il aura perçu
20 + 12 + 10 = 42 €
qui est le prix de vente de sa marchandise;
Ce qui lui fera un bénéfice de
42 – 24=18 € (Bénéfice = prix de vente – prix d’achat)
C’est le bénéfice qu’il ferait selon notre supposition de départ. Or il fait un bénéfice de 198 € c’est à dire un bénéfice 198 : 18 = 11 fois plus important. Donc il a acheté une quantité 11 fois plus importante de marchandise que 12 kg soit
12 x 11 = 132 kg.
On aurait pu choisir n’importe quel nombre pour notre supposition de départ autre que 12. Mais le choix de 12 n’est pas anodin. Comme la masse des tomates est égale à 1/3 de la masse totale et la masse des pommes est égale à 1/4 de la masse totale soit en réduisant au même dénominateur respectivement 4/12 et 3/12. La totalité de la marchandise sera de 12/12.
Voyons avec l’algèbre de quelle manière on résoudrait ce problème.
Nous n’avons pas simplifié les fractions car ce n’était pas judicieux. Mais au lieu de calculer avec des douzièmes on aurait pu le faire avec des sixièmes.
Quatrième 1960
.Effectuer les opérations suivantes :
Exercice 1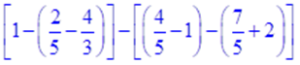
Exercice 2![]()
Execice 3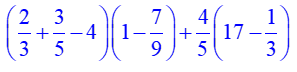
Exercice 4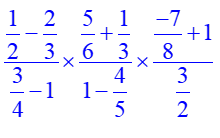
Soit un triangle ABC rectangle en A et sa hauteur AH; on mène de B et C les tangentes BD et CE au cercle de centre A et de rayon AH.
1- Montrer que les points D, A et E sont en ligne droite et que les tangentes BD et CE sont parallèles.
2- Montrer que le cercle de diamètre BC est tangent en A à DE.
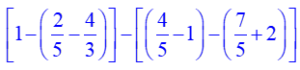 La première chose qu’on remarque, on a une série d’addition ou de soustraction de plusieurs fractions. Or pour additionner ou soustraire des fractions, on doit tout d’abord les réduire au même dénominateur. On pourrait prendre 15 comme dénominateur commun pour les fractions entre les deux crochets. Mais, on ne sait jamais, on prendra donc 15 comme dénomintaure commun pour les fractions du premier crochet et 5 pour les fractions du second crochet. Tout cela se fait, bien sûr de tête.
La première chose qu’on remarque, on a une série d’addition ou de soustraction de plusieurs fractions. Or pour additionner ou soustraire des fractions, on doit tout d’abord les réduire au même dénominateur. On pourrait prendre 15 comme dénominateur commun pour les fractions entre les deux crochets. Mais, on ne sait jamais, on prendra donc 15 comme dénomintaure commun pour les fractions du premier crochet et 5 pour les fractions du second crochet. Tout cela se fait, bien sûr de tête.
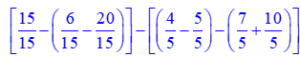 Dans le premier crochet on a une parenthèse qu’on supprime, mais comme elle est précédée du signe – on change les signes des termes qui sont à l’intérieur de cette parenthèse.
Dans le second crochet on additionne les fractions de chacune des parenthèses.
Dans le premier crochet on a une parenthèse qu’on supprime, mais comme elle est précédée du signe – on change les signes des termes qui sont à l’intérieur de cette parenthèse.
Dans le second crochet on additionne les fractions de chacune des parenthèses.
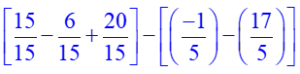 On additionne les fractions du premier crochet que l’on supprime, puis on additionne les fractions du second crochet que l’on supprime aussi.
On additionne les fractions du premier crochet que l’on supprime, puis on additionne les fractions du second crochet que l’on supprime aussi.
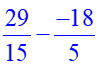 Il faut réduire au même dénominateur 15 et comme la seconde fraction est précédée du signe moins, comme pour une parenthèse, on change le signe de la fraction.
Il faut réduire au même dénominateur 15 et comme la seconde fraction est précédée du signe moins, comme pour une parenthèse, on change le signe de la fraction.
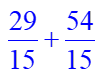 Il ne reste plus qu’à additionner les deux fractions.
Il ne reste plus qu’à additionner les deux fractions.
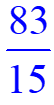 Exercice 2
Exercice 2

D,A,E alignés
Toute tangente à un cercle est perpendiculaire au rayon du cercle aboutissant au point de tangence.
La droite BC est coupe le cercle rouge en un seul point H et elle est perpendiculaire au rayon AH. BC est donc tangente en H au cercle rouge.
La droite passant par un point extérieur au cercle et par le centre du cercle est la bissectrice de l’angle formé par les deux tangentes au cercle issues de ce point.
BH et BD sont les deux tangentes au cercle rouge issues du point B. A étant le centre du cercle, AB est la bissectrice de de l’angle formé par les deux tangentes BD et BH.
Il en est de même pour les tangentes CH et CE. dont Ac est la bissectrice de l’angle qu’elles forment.
Nous pouvons donc écrire après avoir noté les angles B1, B2 puis C1, C2.![]()
Le triangle ABC est rectangle en A et comme la somme des angles d’un triangle est égale à 180°
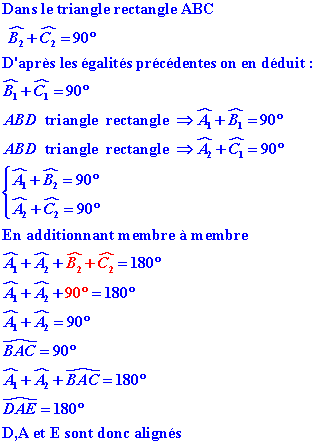
BD et CE parallèles

Sujets d'examens
Premier exercice
Question 1
Nous savons que le carré d’un nombre est nécessairement positif ou nul.![]()
![]()
Le fait que la somme des deux carrés soit égale à 0 peut se traduire par l’égalité suivante :![]()
Ce qui signifie que le nombre A2 est l’opposé de B2. Comme B2 est positif, cela signifie que A2 devrait être négatif, ce qui est impossible pour un carré.
Les deux carrés sont donc nuls.![]()
Question 2![]()
D’après la première question la somme des deux carrés est nulle si chacun des carrés est égal à 0.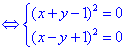
Si le carré d’un nombre est égal à 0, le nombre est égal à 0. Autrement dit la racine carrée de 0 est 0.![]()
On a donc un système de deux équations à deux inconnues. On a le choix entre plusieurs méthodes pour le résoudre. La plus simple dans ce cas est d’additionner membre à membre les deux équations. Après réduction, on obtient l’équation :![]()
Dont la solution est évidemment 0.![]()
Reportons cette valeur de x dans la première équation du système :![]()
En remplaçant x par sa valeur on obtient :![]()
d’où :![]()
Second exercice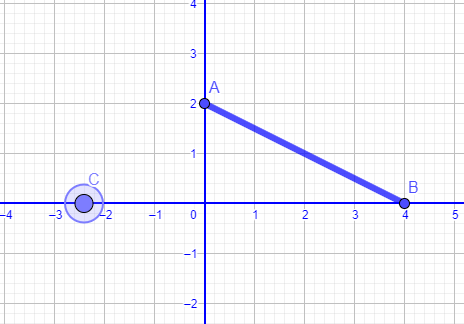
Calcul de AB
Il existe deux manières de calculer la longueur du segment AB.
1) le triangle OAB est un triangle rectangle. D’après le théorème de Pythagore on peut écrire :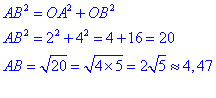
2) on utilise la formule donnant la longueur d’un segment d’après les coordonnées de ses extrémités.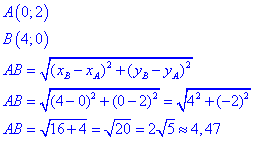
Calcul de l’abscisse de C pour que ABC soit isocèle de sommet B.
Pour que le triangle ABC soit isocèle de sommet B, il faut et il suffit que BC=AB.
Là aussi deux solutions s’offrent à nous.
1)![]()
O,B et C sont alignés sur l’axe des abscisses. BC est égal à BO+OC. Mais il faut tenir compte du sens de ces deux segments c’est pourquoi on utilise la notation de la mesure algébrique, notion plus utilisée aujourd’hui.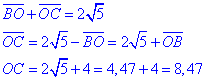
On obtient l’abscisse du point C lorsque C est à droite du point B.
Lorsque C est à gauche du point B, BO et OC sont tous les deux dans le sens négatifs de droite à gauche et on peut écrire :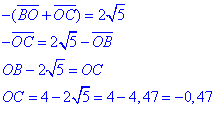
Valeur approchée de 2 racine de 5, : on n’avait pas de calculatrice en 1961, elles n’existaient pas encore mais on devait connaître par coeur quelques racines carrées :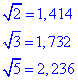
2) On utilise la formule donnant la longueur d’un segment qu’on peut traduire avec les carrés plutôt qu’avec les racines carrées. Ainsi :![]()
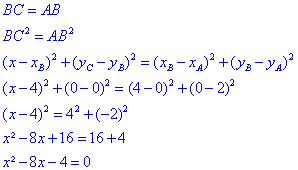
On obtient une équation du second degré. On calcul delta, mais comme b est paire b’ est la moitié de b on utilise la formule :
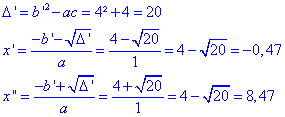
On trouve bien deux points C dont les abscisses sont -0,47 et 8,47.
Calcul de l’abscisse de C pour le triangle ABC isocèle de sommet C.
On utilisera la seconde méthode :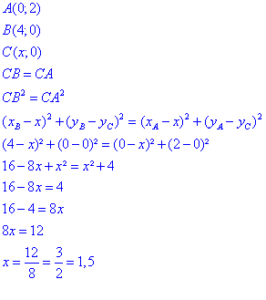
Construction graphique.
Pour construire les deux points C de la deuxième question, puisque BA=BC, les points seront à l’intersection du cercle de centre B et de rayon BA et de l’axe des abscisses.
Pour la troisième question le point C est tel que CA=CB. Le point C est équidistant des extrémités du segment AB, il sera sur la médiatrice de ce segment et puisqu’il appartient à l’axe des abscisses, il se situera à l’intersection de ces deux droites.
Ci-dessous tu peux déplacer le point C avec la souris. Pour afficher les résultats cocher l’une des cases.
Algèbre
Question 1 Développer l’expression A![]()
On remarque deux choses :
en rouge une identité remarquable qu’on devra développer.
En vert un produit de facteurs qu’on devra aussi développer. Comme on a un signe – devant ce produit, on va le garder et mettre le résultat du développement entre parenthèse. ![]()
On distribue 3 dans la première parenthèse. On supprime la deuxxième parenthèse en changeant les signes des termes à cause du signe – devant.![]()
On réduit pour aboutir au résultat :![]()
Question 2 Factorisation de A![]()
On laisse la parenthèse rouge puisque l’identité remarquable est , ici, sous forme factorisée.
On peut intervertir les termes d’une somme, on interverti donc les deux termes en noir.
Plus compliqué: 2-x est l’opposé de x-2. On peut écrire (2-x)=-(x-2) On remplace ce 2-x par sa nouvelle valeur en ajoutant un crochet pour ne pas se tromper.![]()
les termes en noirs constituent une identité remarquable développée dont on va écrire la forme factorisée.![]()
Et miracle, apparâit un facteur commun.![]()
On factorise et on calcule.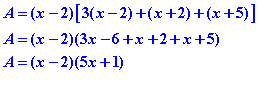
Simplification de la fraction F![]()
Cette fraction n’existe que si son dénominateur est différents de 0 puisque la division par 0 n’a aucun sens.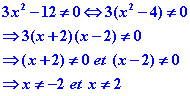
Remplaçon le numérateur par la forme factorisée calculée dans la deuxième question pour la valeur de A.
Remplaçon aussi le dénominateur par sa forme factorisée calculée ci-dessus.![]()
On peut simplifier par x-2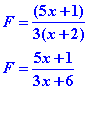
Différentes valeurs de F
Pour x=2![]()
Pour x=moins un cinquième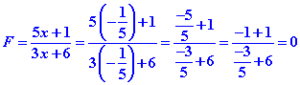
Pour x= racine de 3![]()
Mais on ne peut pas en rester là car il faut rendre le dénominateur rationnel, c’est-à-dire sans radical, sans signe de la racine. Pour cela on multipli le numérateur et le dénominateur de la fraction par la quantité conjuguée du dénominateur.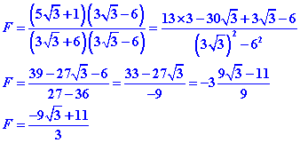
https://www.geogebra.org/m/xpu7xyxsPour déplacer le point M sur le demi cercle : maintenir le clic gauche de la souris sur le point M tout en la déplaçant.
Pour faire apparâitre les constructions supplémentaires cocher les cases en haut à gauche.
Par hypothèse on sait que :
O est le centre du demi cercle.
AB est son diamètre et AB=2R
OM est un rayon du demi cercle
MP est parallèle à AB
I est le milieu de AM
IJ est parallèle à AB
J est un point du segment AP
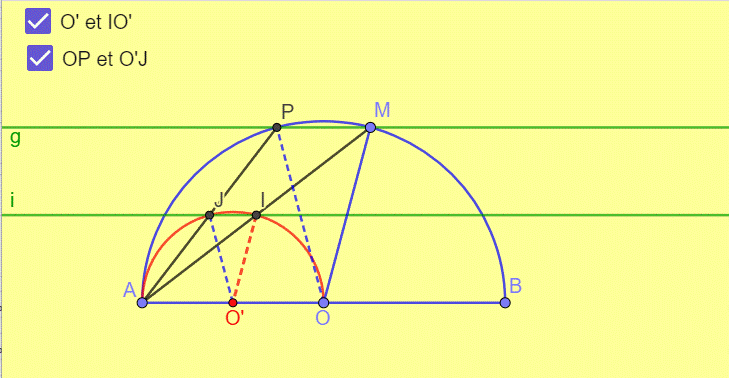
I décrit le cercle (C) de diamètre AO
Construison le point O’ milieu de AO
I est le milieu de AM (par hypothèse)
Dans le triangle AOM O’I joint les milieux des côtés AM et AO
Le segment qui joint les milieus de deux côtés d’un triangle est parallèle au troisième côté et égal à sa moitié.
AInsi quelle que soit la position du point M sur le demi cercle on aura toujours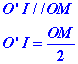
Donc le point I décrira le demi cercle de centre O’ et de diamètre AO en même temps que le point M décrit le cercle de centre O et de diamètre AB
J est un point du cercle (C)
Par hypothèse nous avons![]()
Si deux droites sont parallèle à une m^me troisième, elles sont parallèles entre elles.
Nous en déduisons que les droites PM et IJ sont parallèles.
Comme I est le milieu de AM, IJ est donc le segment qui joint les milieux du triangle APM
J est donc le milieu de AP
Puisque O’ est le milieu de AO
et que J est le milieu de AP
On en déduit que O’J et OP sont parallèles d’après le théorème de la droite des milieus d’un triangle.
Comme P est sur le demi cercle de diamàtre AB, OP est donc un rayon de ce demi cercle.![]()
J est donc bien un point du demi cercle (C).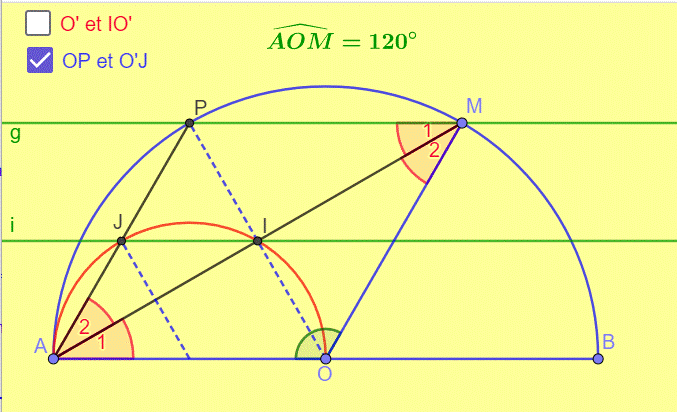
Les droites MP et IJ sont parallèles puisque toutes deux parallèles à AB. On l’a déjà démontré.
OA est un rayon du demi-cercle ainsi que OM donc OA=OM
Le triangle AOM qui possède deux côtés égaux est donc isocèle.
Les deux angles de sa base sont égaux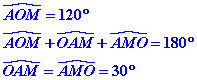
Les droites parallèles PM et AB coupées par la sécante AM interceptent des angles alternes internes égaux. Ce sont les angles rouges 1.![]()
Nous savons que les angles au centre ont même mesure que l’arc qu’ils interceptent et que les angles inscrits mesurent la moitié de l’arc intercepté.
Nous pouvons donc écrire.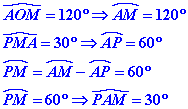
Nous en déduisons l’égalité des deux angles rouges 2![]()
Or ces deux angles égaux interceptent deux droites AP et MO coupées par une sécante AM. Ces deux droites sont donc parallèles.
AInsi les côtés PM et AO du quadrilataire AOMP sont parallèles.
ses côtés AP et MO sont aussi parallèles.
Un quadrilataire dont les côtés opposés sont parallèles est un parallélogramme.
D’autre part OA=OM
Un parallélogramme dont deux côtés consécutifs sont égaux est un losange.
Le quadrilataire APMO est un losange.
OI passe par le point P
Les diagonales d’un losange se coupent en leur milieu Elles sont perpendicuaires.
I est le milieu de AM
I est le point de concours des diagonales du losange.
OP est une diagonale dont le milieu est I.O,I,P sont alignés.
Donc OI passe par P.
Puissance du point P par rapport au demi cercle.
Cette notion de puissance d’un point n’est plus étudié ni dans les collèges ni dans les lycées.
Aussi en voici la définition.
Soit un point A à l’extérieur ou à l’intérieur d’un cercle (c).
Soit droite passant par A et sécante en B et C au cercle c
Soit Les deux tangentes au cercle passant par A et coupant le cercle en T et T’
La puissance du point A par rapport au cercle c est le nombre ABxAC qui est aussi égal à AT².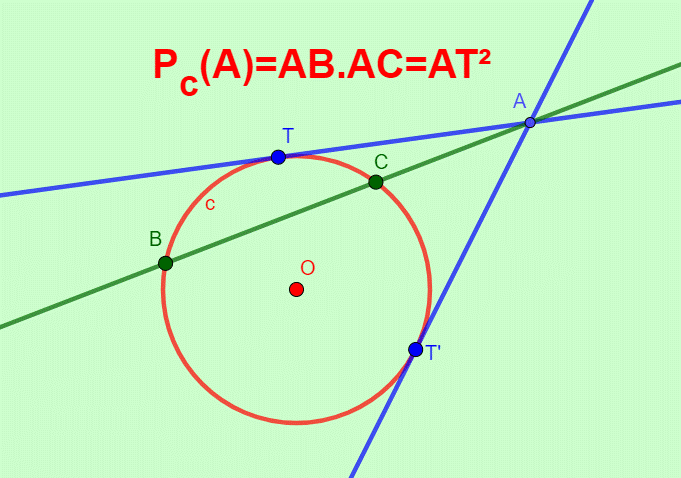
Reprenons notre figure.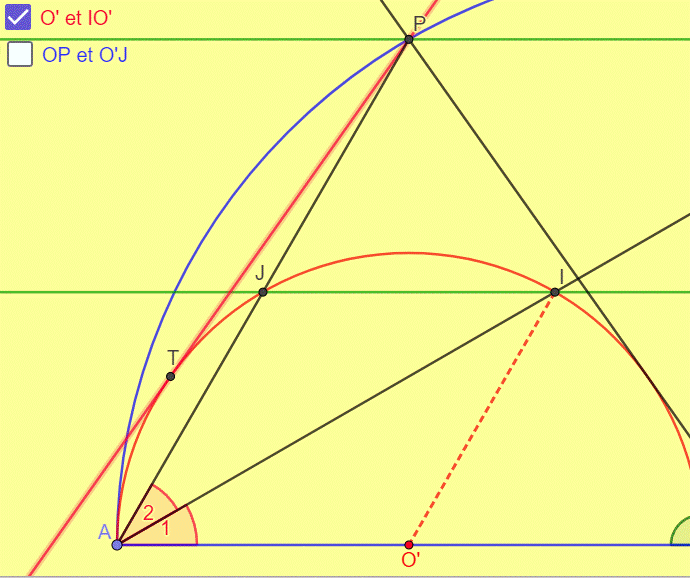
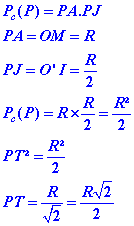
![]()
Il s’agit de trouver la ou les valeurs de x vérifiant cette équation et telles qu’elles soient comprises entre o et π.
Nous savons d’après les formules trigonométriques que :![]()
et donc que :![]()
Remplaçons dans l’équation de départ et continuons les calculs par une factorisation :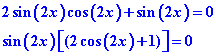
Nous obtenons une équation produit nul :
Nous avons donc deux solutions pour cette équation :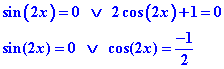
Or O est le sinus de l’angle Π et -1/2 est le cosinus de l’angle 2Π/3. Nous pouvons donc écrire :![]()
Pour le sinus et le cosinus nous savons que :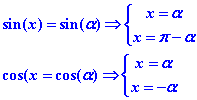
Pour le sinus nous aurons deux solutions :
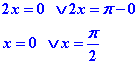
et deux solutions pour le cosinus :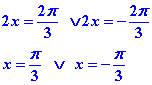
Compte tenu des restrictions de l’énoncé, nous aurons le résultat suivant :
Calcul du produit scalaire
Le produit scalaire de deux vecteurs dont on connaît les composantes ( coordonnées) est égal à la somme du produit des abscisses et du produit des ordonnées.![]()
Nous connaissons les coordonnées des points A,B et M :
Nous en déduisons les composantes des vecteurs MA et MB :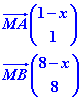
Et nous pouvons calculer leur produit scalaire :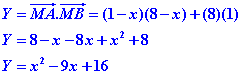
On obtient une équation du second degrés. Le produit scalaire des deux vecteurs prend la valeur donnée par cette équation lorsque x varie.
Signe du produit scaliare :
On doit maintenant étudier le signe du produit scalaire qui sera le signe du trinôme du second degrés précédent suivant les valeurs de x.
Calcul du discriminant et des racines du trinôme :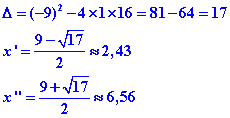
Tableau de signes
Nous en déduisons la valeur de l’angle AMB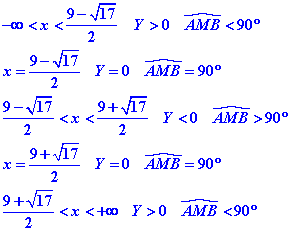
Construction géométrique simple
Lorsque Y=0, le point M est tel que l’angle ![]() .
.
Il est donc inscrit dans un demi cercle de diamètre AB et de centre I0 milieu de AB
Ce cercle coupe l’axe des abscisses en M’0 et M »0.![]()
Calcul du cosinus de l’angle AMB
Utilisons une autre formule du produit scalaire : c’est le produit des normes (longueurs) des vecteurs et du cosinus de l’angle qu’ils forment.![]()
On en déduit la valeur du cosinus :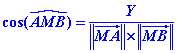
Nous connaisons :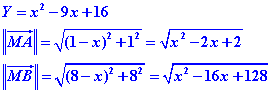
Donc :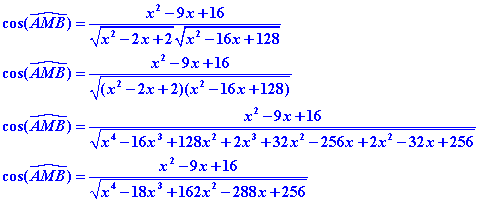
Calcul de l’angle pour x=4
Il suffit dans la formule précédente de remplacer x par 4 :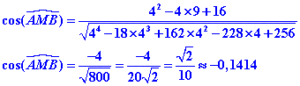
Avec une calculatrice on trouve un angle de 98,13° c’est à dire 98 degrés et 13 centièmes de degrés et non pas des minutes.
Avec l’extrait de la table trigonométrique donnée par l’énoncé, on voit que 0,1414 est compris pour les sinus entre 0,1564 et 0,1392 ce qui correspondrait à un angle compris entre 8 et 9°.Or nous avons obtenus un cosinus.
On utilisera les formules trigonométriques :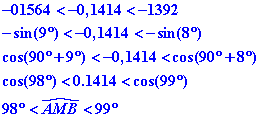
Ordonnée du point I :
I appartient à la médiatrice de AB
I0 est le milieu de AB.
II0 et AB sont orthogonaux.
Le produit scalaire de ces deux vecteurs est donc égal à 0.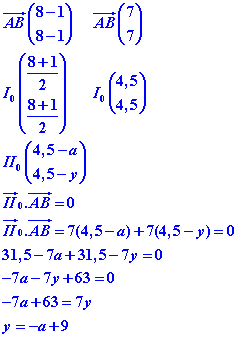
Equation du cercle C de centre I et passant par A et B.
Tous les points N du cercle de coordonnées (x,y) sont à égale distance du centre du cercle.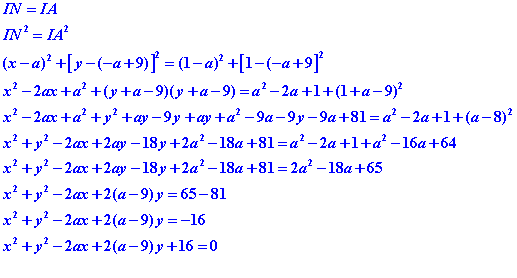
Intersection du cercle C avec l’axe des abscisses :
Lorsque le cercle coupe l’axe des abscisses , les points d’intersection ont pour ordonnées y=0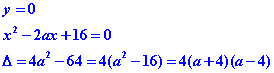
Le cercle C coupera l’axe des abscisses en deux points si Δ est positif .
Il coupera l’axe en un seul point si Δ est nul. Le cercle sera tangent à l’axe des abscisses.
Le cercle ne coupera pas l’axe des abscisses si Δ est négatif .




