Fonctions composées
Exemple concret
Je possède un chauffage à pompe à chaleur.
Ma consommation d’électricité journalière , donc ma dépense en euro de chaque jour dépend de la température extérieure. Elle est de cet ordre :
\(P=0,6 t\) t étant l’écart entre les températures extérieures et intérieures (23°)
Mais la température extérieure dépend du jour de l’année où on se trouve.
Ainsi, on peut établir le schéma suivant :
Nous avons deux fonctions,
La première nous donne la température extérieure en fonction du jour de l’année.
La seconde nous donne notre dépense énergétique en fonction de la température extérieure.
Il nous serait possible de connaître directement notre consommation énergétique en fonction du jour de l’année.
On vient de définir une fonction composée :
La dépense énergétique donnée en fonction du jour de l’année peut être décomposée en deux fonctions :
l’une donnant la température extérieure en fonction du jour de l’année, l’autre donnant la dépense en fonction de la température extérieures.
Ci dessous, les deux fonctions pour des journées du mois de mai 2025 et janvier 2026:
au dessus la température extérieure selon le jour de l’année,
au dessous la dépense journalière en énergie.
Premier exemple
La fonction \(h(x)\) est le résultat de la composition de deux autres fonctions \(f(x)\) et \(g(x)\). On commence à appliquer la fonction \(f(x)\), puis on applique au résultat la fonction \(g(x)\).
Soit la fonction h
Elle consiste à prendre le carré d’un nombre quelconque \(x\) auquel on a rajouté 2.
Pour trouver la valeur du nombre \(h(x)\) en partant de \(x\) on procède en deux étapes.
Coche « Afficher l’étape 1 ».
au nombre \(x\) quelconque on rajoute 2
Fait glisser le point marron situé sur l’axe des x vers la droite jusqu’à 10.
Ce point désigne la valeur de \(x\)
On voit s’afficher progressivement en ordonnées la valeur de \(x+2\)
Ramène le point marron vers -10 et coche la case » Afficher l’étape 2″.
Puis fait glisser le point marron à nouveau vers +10.
On voit s’afficher progressivement en ordonnées les valeurs du carré du nombre \(x+2\).
Ainsi on a utilisé deux fonctions.
Avec la première qu’on appellera \(f(x)\), on ajoute le nombre 2 à un nombre \(x\) quelconque. On obtient un résultat que nous appellerons \(X\).
Avec la seconde qu’on, appellera \(g\), on élève au carré le résultat \(X\) de la première.
On a ainsi composé deux fonctions \(f\) et \(g\) pour obtenir la fonction \(h\) .
En composant entre elles les fonctions \(f\) et \(g\), on obtient la fonction\(h\).
Par la fonction \(g\), on prend le carré d’un nombre calculé avec la fonction \(f\) .
On commence par appliquer la fonction \(f\) pour ensuite appliquer la fonction \(g\) au résultat de \(f\)
Deuxième exemple
La fonction \(h(x)= ln(x^2+1)\) peut être décomposées en deux fonctions.
La première \(f(x)\) :
A tout nombre x de l’ensemble des nombres réels on fait correspondre son carré auquel on ajoute 1 :\( x²+1\).
\(f(x)=x²+1\)
Si on nomme \(X\) ce résultat \(X=x²+1\).
la seconde fonction \(g(X)\) consiste à prendre le logarithme du résultat \(X\) de la première fonction \(f(x)\).
\(g(X)=ln(X)=ln(x²+1)\)
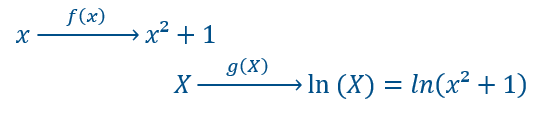
Définition
cette expression se lit \( h \) égale \(f\) rond \(g\),
\(f\) suivi de \(g\) ou \(g\) après \(f\).
Trouver les fonctions d'une composition de fonctions
Soit la fonction \(h(x)=\frac{1}{x^2+1}\), c’est une fonction composée. En effet en partant de \(x\) on le transforme en \(x^2+1\) grâce à une fonction \(f(x)=x^2+1\). Puis grâce à une autre fonction \(g(x)\), la fonction inverse \(g(x)=\frac{1}{x}\), on transforme \(x^2+1\) en son inverse pour obtenir \(h(x)=\frac{1}{x^2+1}\)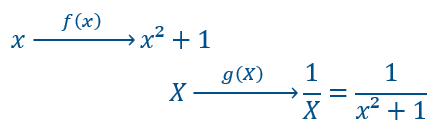
Soit la fonction \(h(x)=e^{x^2-3x+4}\). C’est une fonction composée. Pour un nombre quelconque \(x\) on commence par le transformer en \(x^2-3x+4\) grâce à la fonction \(f(x)=x^2-3x+4\) puis on transforme le nombre obtenu en prenant son exponentielle grâce à la fonction \(g(x)=e^x\).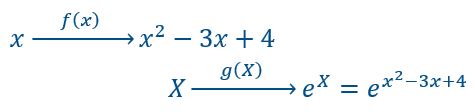
Composer deux fonctions
Soient les fonctions :
\((f(x)\) et \(g(x)\) :
\(f(x)=x^2+x+3\) et \(g(x)=\frac{3x}{x+1}\)
Calculons \(g∘f\)
on sait que \(g∘f=g(f(x)\)
la variable de \(f\) est \(x\), variable indépendante, mais la variable de \(g\) est \(f(x)=x^2+x+3\) écrite en rouge. c’est une variable dépendante puisqu’elle dépend dela fonction \(f\).
Dans \(g\), il suffit de remplacer \(x\) par cette nouvelle variable.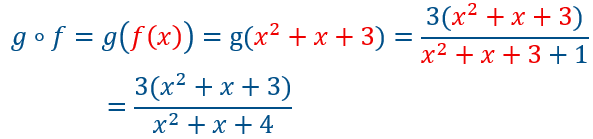
Calculons \(f∘g\)
on sait que \(f∘g=f(g(x))\)
la variable de \(g\) est \(x\), mais la variable de \(f\) est \(g(x)=\frac{3x}{x+1}\) écrite en rouge.
Dans \(f\), il suffit de remplacer \(x\) par cette nouvelle variable.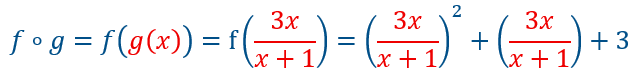
Propriétés des compositions de fonctions.
En prenant les deux fonctions du paragraphe précédent :
\(f(x)=x^2+x+3\) et \(g(x)=\frac{3x}{x+1}\)
\(g\circ f\neq f\circ g\)
\(f\circ g=f(g(x))=\left ( \frac{3x}{x+1} \right )^{2}+\frac{3x}{x+1}+3\)
\(g\circ f=g(f(x))=\frac{3(x^2+x+3)}{x^2+x+4}\)
Soient les fonctions :
\(f(x)=2x\) \(g(x)=x^2 \) \(h(x)=ln(x)\)
Calculons
\( h\circ (g\circ f)=h\circ (g(f(x)))=\)
\(h\circ (g(2x))=h\circ ((2x)^2)=ln((2x)^2)=ln(4x^2)\)
Calculons ensuite \( (h\circ g)\circ f=h(g(x))\circ f=h(x^2)\circ f=\)
\(ln(x^2)\circ f=ln((2x)^2)=ln(4x^2)\)
Prenons les mêmes fonctions que précédemment :
\(f(x)=2x\) \(g(x)=x^2 \) \(h(x)=ln(x)\)
soit comme opération l’addition des fonctions par exemple :
Calculons
\(h\circ (g+f)=h\circ (x^2+2x)=ln(x^2+2x)\)
Calculons
\((h\circ g)+(h\circ f)=h\left [ g(x) \right ]+h\left [ f(x) \right ]=\)
\(ln(x^2)+ln(2x)\)
Il est évident que
\(ln(x^2+2x)\neq ln(x^2)+ln(2x)\)
soient les fonctions
\(f(x)=\frac{1}{x}\) et \(g(x)=x^2 \)
La fonction \(f\) est continue pour tout \(x\) différent de 0
La fonction \(g\) est continue pour tout \(x\)
La fonction composée \(g\circ f=g\left [ f(x) \right ]=g(\frac{1}{x})=\left ( \frac{1}{x} \right )^2\) est continue pour tout \(x\) différent de 0.
Dérivée d'une fonction composée
C’est relativement compliqué à expliquer mais relativement simple à pratiquer lorsqu’on a compris le principe.
Ci-dessous les différentes définitions de la dérivée d’une fonction composée. Nous considérerons une fonction composée non dénommée de deux fonctions \(f(x)\) et \(g(x)\).
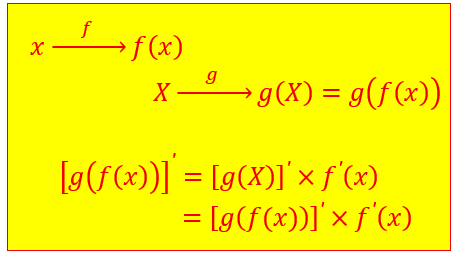
On peut aussi apprendre par coeur le tableau ci-dessous :
Soit la fonction \(h(x)=(4x^2+5x-2)^5\).
C’est une fonction composée de deux fonctions :
\(f(x)=4x^2+5x-2\) et \(g(x)=x^5\) qu’on peut aussi écrire pour la seconde \(g(X)=X^5\) avec \(X=4x^2+5x-2\).
Cette fonction composée peut être schématisée de la façon suivante :
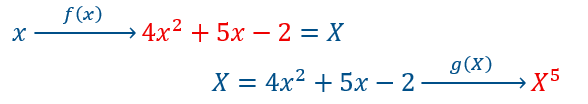
Nous avons noté en rouge les deux expressions à dériver.
La dérivée de cette fonction composée est égale aux produit des deux dérivées en rouge.
\(h'(x)= g'(X)\times f'(x)=5X^4\times (8x+5)\)
En remplaçant \(X\) par sa valeur, on obtient l’expression de la dérivée de notre fonction composée :
\(h'(x)= g'(X)\times f'(x)=5(4x^2+5x-2)^4\times (8x+5)\)
Soit la fonction \( f(x)=e^{\frac{1}{x}}\).
C’est une fonction composée des deux fonctions : \(u(x)=\frac{1}{x}\) et \(v(x)=e^{x}\) ou \(v(X)=e^{X}\) avec \(X=\frac{1}{x}\).
On peut schématiser cette fonction de la façon suivante :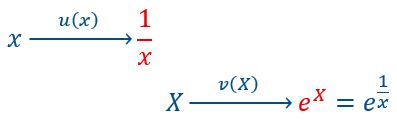
Comme précédemment les expressions à dériver sont écrites en rouge.
La dérivée de \(f(x)\) est égale au produit des deux dérivées écrites en rouge :
\(f'(x)=u'(x)\times v'(X)\), soir
\(f'(x)=\left ( \frac{1}{x} \right )’\times \left ( e^{X} \right )’ \)
Donc : \(f'(x)=\left ( -\frac{1}{x^2} \right )\times e^{X}\) puisque la dérivée d’une fonction exponentielle est la fonction exponentielle elle-même.
En remplaçant \(X\) par sa valeur, nous obtenons la dérivée de notre fonction.
\( f'(x)=\left ( -\frac{1}{x^2} \right )\times e^{\frac{1}{x}}\)
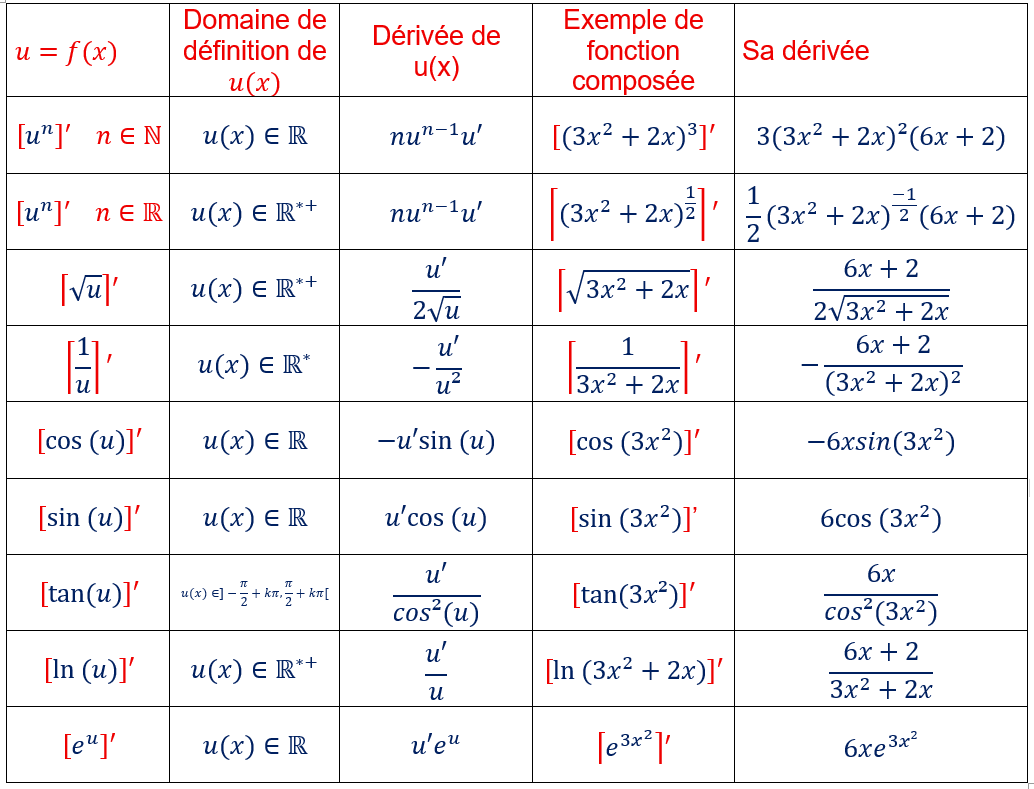
le même tableau avec les fonctions réciproques des fonctions trigonométriques circulaires et les fonctions trignométriques hyperboliques.
Primitive d'une fonction composée
Technique et exemple
Calculer une primitive est une opération inverse de celle qui consiste à calculer une dérivée.
Pour une fonction composée
\(h(x)=g(f(x)\), nous avons vu que la dérivée de
\(h(x)\)
était égale au produit de la dérivée de
\(g(x)\) par rapport à \(f(x)\) soit \(g'(f(x)\)
par la dérivée de \(f(x)\) par raport à \(x\) soit \(f'(x)\).
S nous rencontrons une fonction qui est le produit de deux fonctions
\(f(x)\) et \(g(x)\) dont
l’une \(f(x)\) est la dérivée de l’autre \(g(f(x))\) nous pouvons en déduire que sa primitive est \(g(f(x))\).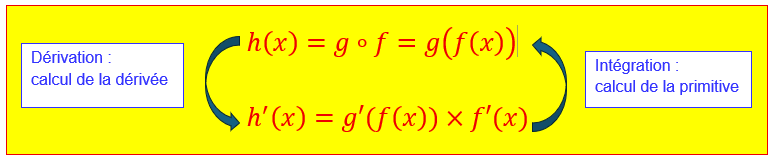
La primitive d’une fonction
\(h(x)\)
constituée du produit de deux fonctions
\(f(x)\) et \(g(x)\)
dont l’une
\(f(x)\) est la dérivée de l’autre
\(g(f(x))\) est une fonction composée
\(h(x)=g(f(x))\).
UneSoit la fonction:
\( h(x)=3x^2(x^3+2)^2\).
Nous remarquons que
\( f(x)=(x^3+2)\) et que
\(f’x)=3x^2 \) alors que
\(g(x)=(x^3+2)^2\). Cette situation correspond bien à la dérivée d’une composition de fonction. Une primitive de cette dérivée de composition de fonction sera donc :
\(H(x)=\frac{(x^3+2)^{2+1}}{2+1}+cte\) soit :
\( H(x)=\frac{(x^3+2)^{3}}{3}+cte\).
Si on calcule la dérivée de ce résultat on retrouvera notre fonction de départ \(h(x)\).
Nous aurions la même démarche avec la fonction suivante :
\( h(x)=\frac{3x^2}{(x^3+2)^2}\)
qui peut s’écrire :
\(h(x)=3x^2\frac{1}{(x^3+2)^2}\)
mais encore avec les exposants négatifs :
\(h(x)=3x^2(x^3+2)^{-2} \)
La primitive d’une telle fonction sera donc :
\(H(x)=\frac{(x^3+2)^{-2+1}}{-2+1}+cte\)
\(H(x)=\frac{(x^3+2)^{-1}}{-1}+cte \)
\(H(x)=-\frac{1}{(x^3+2)} +cte\)
Nous aurions pu utiliser la formule à la place de la technique des exposants négatifs.
Autres exemples
Soit la fonction :
\(h(x)=\frac{2x}{(x^2+3)^2}\)
\(h(x)=2x\frac{1}{(x^2+3)^2}\)
nous remarquons que :
\(f(x)=x^2+3\)
\(f'(x)=2x\)
\(g(x)=\frac{1}{(x^2+3)^2}\)
que nous pouvons écrire avec les exposants négatifs :
\(h(x)=2x(x^2+3)^{-2}\)
une primitive sera donc
\(H(x)=(x^2+3)^{-2+1}+cte\)
\(H(x)=(x^2+3)^{-1}+cte\)
\(H(x)=\frac{1}{x^2+3}+cte\)
Soit la fonction :
\(h(x)=\frac{2x}{x^2+3}\)
\(h(x)=2x\frac{1}{x^2+3}\)
nous remarquons:
\(f(x)=x^2+3\)
\(f'(x)=2x \)
\(g(x)=\frac{1}{x^2+3}\)
\(g(x)=(x^2+3)^{-1}\)
En utilisant les exposants négatifs, on trouve un exposant nul pour la primitive. Mais nous savons que la primitive de
\( \frac{1}{u}\) est \(ln(u)\)
Donc :
\(H(x)=ln(x^2+3)+cte\)
Soit la fonction :
\(h(x)=(8x+5)e^{4x^2+5x-3}\)
Nous remarquons :
\(f(x)=4x^2+5x-3\)
\(f'(x)=8x+5\)
\(g(x)= e^{4x^2+5x-3}\)
Nous en déduisons :
\(H(x)= e^{4x^2+5x-3}+cte\)
Soit la fonction :
\(h(x)=-\frac{1}{x^2}cos(\frac{1}{x})\)
Nous remarquons :
\(f(x)=\frac{1}{x}\)
\(f'(x)=-\frac{1}{x^2}\)
\(g(x)=cos(\frac{1}{x})\)
Nous en déduisons :
\(H(x)=sin(\frac{1}{x})+cte\)
Tableau des primitives
Lorsque la dérivée n'est pas complètement explicite
Soit la fonction
\(h(x)=a(ax+b)^n\)
on remarque
\(f(x)=ax+b\)
\(f'(x)=a\)
\(g(x)=(ax+b)^n\)
Dans ce cas une primitive sera :
\(H(x)=\frac{1}{n+1}(ax+b)^{n+1}+cte\)
\(h(x)=(ax+b)^n\)
On remarque :
\(f(x)=ax+b\)
\(f'(x)=a\)
\(g(x)=(ax+b)^n\)
Or a est absent.
Pour le faire apparaître il suffit de multiplier \(h(x)\) par a. Mais pour ne pas changer la valeur de \(h(x)\) il faut diviser par a en même temps.
\(h(x)=\frac{a}{a}(ax+b)^n\)
Ce qui peut s’écrire :
\(h(x)=\frac{1}{a}a(ax+b)^n\)
Notre fonction est multipliée par \(\frac{1}{a}\), sa primitive également.
\(H(x)=(\frac{1}{a})(\frac{1}{n+1})(ax+b)^{n+1}+cte\)
d’où :
une primitive de
\(h(x)=(ax+b)^n\) est \(H(x)=(\frac{1}{a})(\frac{1}{n+1})(ax+b)^{n+1}+cte\)
Quelques exemples
\(f(x)=(5x+7)^2\)
\(F(x)=\frac{1}{15}(5x+7)^3\)
\(f(x)=\frac{1}{3}(x+4)\)
\(F(x)=3ln(\frac{1}{3}x+4)\)
\(f(x)=e^{\sqrt3x+9}\)
\(F(x)=\frac{1}{\sqrt3}e^{\sqrt3x+9}\)
\(f(x)=cos(5\pi x+2)\)
\(F(x)=\frac{1}{5\pi }sin(5\pi x +9)\)
Soit la fonction :
\(h(x)=\frac{x}{x^2+3}\)
Nous remarquons :
\(f(x)=x^2+3\)
\(f’x)=2x\)
Mais au numérateur nous n’avons pas la dérivée de cette fonction. Nous allons la faire apparaître en multipliant ce numérateur par 2 tout en divisant aussi par 2 pour ne pas changer la valeur de la fonction.
\(h(x)=\frac{2}{2}\times \frac{x}{x^2+3}\)
\(h(x)=\frac{1}{2}\times \frac{2x}{x^2+3}\)
Ainsi notre fonction est multipliée par un demi, sa primitive le sera aussi.
\(h(x)=\frac{1}{2}\times(x^2+3)^{-2}\)
\(H(x)= \frac{1}{2}\times (x^2+3)^{-2+1}+cte\)
\(H(x)=\frac{1}{2}\times \frac{1}{x^2+3}+cte\)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Soit la fonction :
\(h(x)=\frac{1}{x^2}cos(\frac{1}{x})\)
nous remarquons :
\(f(x)=\frac{1}{x}\)
\(f'(x)=-\frac{1}{x^2}\)
L’expression \(\frac{1}{x^2}\) n’est pas égale à la dérivée \(f'(x)\). Pour qu’elle le soit, il faudrait la multiplier par \(-1\). Mais pour ne pas changer la valeur de la fonction, il sera obligatoire de la multiplier encore une fois par \(-1\). en ne notant pas le 1 qui est l’élément neutre de la multiplication, on obtient :
\(h(x)=-(-\frac{1}{x^2})cos(\frac{1}{x})\)
La fonction est finalement multipliée par -1, sa primitive également.
\(H(x)=-sin(\frac{1}{x})+cte\)
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.