La fonction exponentielle népérien
- par gabriel
- dans Fonctions, Mathématiques
- sur 15 avril 2020

Sommaire
Définition
C’est l’unique fonction qui a pour dérivée la fonction elle-même et qui coupe l’axe des ordonnées en 1.
On la désigne par :![]()
ou :![]()
e désignant un nombre particulier :![]()
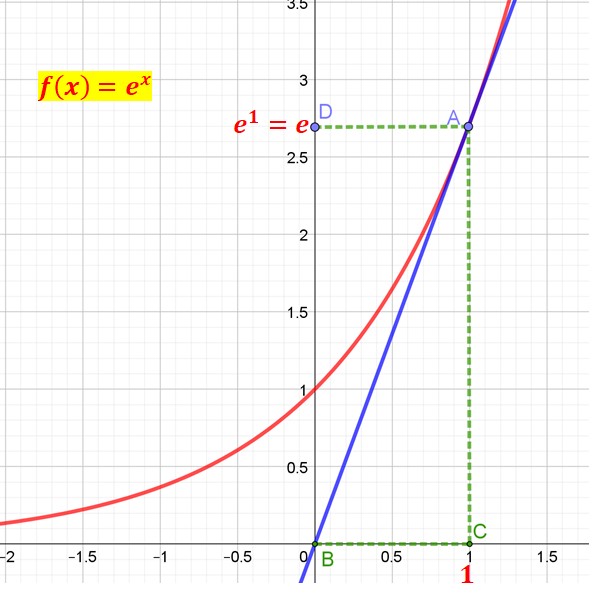
La fonction f(x)=ex est représentée par la courbe rouge. Au point A d’abscisse 1 on a :
Le nombre dérivé au point A est :![]()
Le coefficient directeur de la tangente en A est :
Au point A le nombre dérivé, la pente de la tangente sont bien égaux à la valeur de la fonction.
Est-ce valable pour tous les points de la courbe ?

Commençons par le point I d’abscisse 1,5
Son ordonnée est :![]()
Coordonnées du point I ![]()
Nombre dérivé en I :![]()
Pente de la tangente au point I :
Pour le point A le calcul est fait précédemment sachant que :![]()
Je te laisse le soin de continuer avec les points G,E,L,M.
Des démonstrations
Th 1 :La fonction exponentielle ne s’annule pas sur l’ensemble des nombres réels ℜ.
Soit f une fonction définie sur ℜ telle que :
Soit g une fonction définie sur ℜ telle que :![]()
On calcule sa dérivée :![]()
C’est la dérivée d’un produit. On applique la formule : ![]()
Or f(-x) est une composition de fonctions :
Nous en déduisons :![]()
Or par hypothèse f’=f![]()
Donc :![]()
Si la dérivée de la fonction g est nulle c’est que la fonction g est constante.
D’autre part on sait que :![]()
On en déduit que :![]()
Et puisque la fonction g est constante ![]()
![]()
![]()
Th 1 ![]()
![]()
Th 2 Il n’existe qu’une seule fonction vérifiant les conditions :
Soit deux fonctions f et g vérifiant les conditions suivantes : ![]()
Soit h une fonction telle que : ![]()
Cette fonction h est bien définie sur R puisque nous avons démontré ci-contre qu’une fonction répondant aux conditions de l’hypothèse ne peut pas être égale à 0.
D’autre part la fonction h est dérivable sur R puisqu’elle est le quotient de deux fonctions f et g dérivables sur R .![]()
Or on sait que f’=f et g’=g d’après l’hypothèse :![]()
![]()
Puisque la dérivée de h est nulle, la fonction h est une fonction constante.
Quelle est cette fonction constante ?
On sait que par hypothèse :![]()
donc :![]()
Comme la fonction h est une fonction constante : 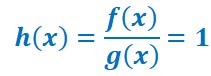
Donc :![]()
Il est donc maintenant évident qu’il n’existe qu’une seule et unique fonction répondant aux conditions initiales.
Th 4 La fonction exponentielle ex est strictement positive sur R.
On peut noter cette fonction f aux propriétés particulières de deux manières différentes :![]()
f de x = exponentielle de x = e puissance x
Ainsi les propriétés se déclinent de la façon suivante :
Nous utiliserons définitivement la notation avec e.
——————————————————————–
Démontrons maintenant notre théorème.
Nous savons que :
Raisonnons par l’absurde :
On suppose que la fonction ex prend une valeur négative pour x=a :![]()
Dans ce cas, on a, à la fois :
![]()
D’après le théorème des valeurs intermédiaires, une fonction continue variant entre une valeur négative et une valeur positive, passe au moins une fois par la valeur 0.
Notre fonction est continue sur R puisqu’elle est dérivable sur R (c’est sa définition). Donc ex = 0 pour une ou plusieurs valeurs de x.![]()
Or c’est impossible puisque nous avons démontré précédemment que cette fonction ne s’annulait jamais. ![]()
On vient de prouver par ce raisonnement par l’absurde que la fonction ex ne pouvait pas être négative, donc elle est toujours positive. ![]()
Autre façon de démontrer la même chose : ![]()
et comme ex ≠ 0
Th4![]()
Puisque ex qui est rappelons le aussi la dérivée de ex est toujours positive, alors la fonction ex est strictement croissante sur R :
Th5![]()
on déduit de ce théorème, d’autres qui permettent de résoudre les équations et les inéquations en ex
Th6.1![]()
Th6.2![]()
Th6.3
Nous ne pouvons pas résoudre toutes les équations de ce genre. Pour cela on a besoin de la notion de Logarithme Népérien, Ln.
Il n’est pas utile de connaître Le théorème 6.3.
En effet, il suffit de remplacer 1 dans le second membre de l’équation par e0. On applique ensuite Th6.1 ou Th 6.2
On peut démontrer que la fonction exponentielle se note ex . Nous ne le ferons pas dans ce chapitre.
Avec cette notation, x est un nombre réel.Par exemple avec eπ , π est un réel mais n’est pas un entier, on ne peut plus dire eπ est le produit π fois de e par lui même !
Th 3 Propriétés algébriques :
quels que soient x et y appartenant à R ![]()
Th3.1 ![]()
A partir de cette assertion on peut écrire :![]()
Comme ey ≠ 0, on peut diviser par ey :
Th3.2
Si x=0
Th3.3
Calculons maintenant :![]()
Démontrons par récurrence que :![]()
Soit n > 0 ou n = 0
Pour n = 0 la propriété est vraie car :![]()
Supposons que cette propriété est vraie pour n > 0.Qu’en est-il pour n+1 ?![]()
Comme la propriété est vraie pour n, on pet écrire : ![]()
D’après la première propriété : ![]()
On factorise l’exposant par x : ![]()
La propriété est vraie pour n positif ou nul.
Soit n < 0
-n > 0
Comme -n >0 on peut utiliser la propriété démontrée précédemment :
Donc :![]()
On vient de démontrer que quel que soit n entier positif ou négatif :
Th3.4![]()
Limites

Fonctions ex et f(x)=ex-x
Tableau de variation de la fonction f 
On déduit :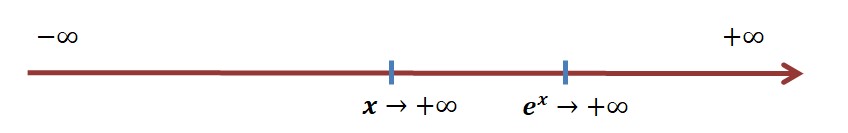

Quelle est la limite de ex quand x tend vers l’infini ?
Il nous faudrait démontrer que quel que soit x appartenant à R ex est plus grand que x.
Ainsi si x tend vers l’infini et que ex>x, ex tendra obligatoirement vers l’infini.
Pour cela, considérons la fonction(en rouge sur le graphique ci-contre)![]() Sa dérivée est :
Sa dérivée est :![]() Elle admet un extremum lorsque sa dérivée s’annule
Elle admet un extremum lorsque sa dérivée s’annule![]()
![]()
![]()
![]()
![]() Cet extremum en 0 est :
Cet extremum en 0 est :![]() D’après les réciproques du théorème 6.3 pour x<0:
D’après les réciproques du théorème 6.3 pour x<0:![]()
![]()
![]()
Donc la fonction f(x) est décroissante.
Pour x >0![]()
![]()
![]() Donc la fonction f(x) est croissante
Donc la fonction f(x) est croissante
Tout ceci est résumé dans le tableau ci-contre. On en déduit : ![]()
![]()
Explications sur les passages entre moins l’infini et plus l’infini :

Maintenant, il faut trouver la limite de ex quand x tend vers moins l’infini.
Pour cela on utilise un petit stratagème que l’on trouve à force de chercher.
Posons :![]()
et ![]()
On en déduit (voir ci contre pour cette égalité :![]()
On peut écrire : 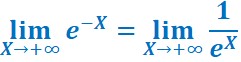
D’après le paragraphe précédent, on sait que :![]()
eX est un très grand nombre puisqu’il tend vers l’infini. Si on divise 1 par ce très grand nombre, on obtient un très petit nombre proche de 0.
Donc : 
Et :![]()
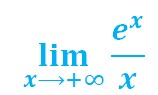
Représentation graphique de la fonction avec sa limite en +∞.

D’autres limites en rapport avec la fonction exponentielles sont utiles à connaître. Par exemple celle ci-contre.
Nous pouvons écrire puisque x tendant vers plus l’infini est forcément plus grand que 0 :
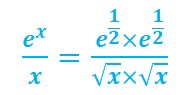
Ce qui se traduit par : 
On sait que![]()
donc ![]()
En divisant par racine de x qui est strictement plus grand que 0 : 
En élevant au carré :
Puis en réduisant :

Comme x tend vers plus l’infini, x divisé par 4 tend vers plus l’infini (Eh oui !!!). ![]()
et donc : ex sur x qui lui est plus grand :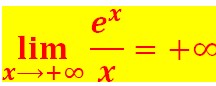

Ci-dessous la représentation graphique de cette fonction avec sa limité : 
C’est une limite encore utile à connaître. En voici la démonstration. ![]()
Soit X=-x :![]()
En effet si x tend vers -∞ X=-x tend vers +∞.
On divise par X qui est différent de 0
d’où évidemment ; 
D’après la limite ci-dessus, on sait que : 
Donc :
le dénominateur tendant vers l’infini, si on divise le numérateur -1 par ce très grand nombre, on obtient un nombre qui s’approche de 0 :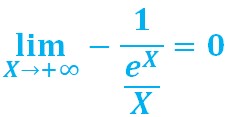
Et : 
Dérivées
Deux façons d’écrire la dérivée de la fonction exponentielle :![]()
![]()
Par définition la dérivée de la fonction exponentielle est la fonction exponentielle elle même. Ci-contre de façons d’écrire mathématiquement cette affirmation.
Mais qu’en est-il de la dérivée d’une fonction composée avec la fonction exponentielle ?
Rappel sur les fonctions composées.

![]()
![]()


Une fonction composée, est une fonction de fonction.
Pour un nombre x on calcule son image par une fonction g, on obtient un résultat g(x)=u. On calcule ensuite l’image de ce résultat par la fonction f : f(g(x))=f(u).
Il existe de manières de’écrire mathématiquement une fonction composée qu’on lit :
f de g de x ou
f rond g de x
Voir la notation ci contre.
On commence par appliquer g puis ensuite f.
La dérivée d’une fonction composée ![]()
est égale au produit de la dérivée de g par rapport à x par la dérivées de f par rapport à g(x),![]()
ou su u= g(x)![]() .
.
Pour la fonction donnée dans le tableau :![]()
On résout de la manière suivante :
On procède de cette façon avec une fonction composée ayant une fonction exponentielle, sachant que la dérivée de la fonction exponentielle est la fonction elle-même.
Primitives
Primitive de ![]()
![]()
Il est évident que comme la dérivée de la fonction ex est la fonction elle même, sa primitive sera aussi la fonction elle-même à une constante k près. Rappelons que si une fonction est désignée par f(x), sa primitive s’écrit F(x).
Primitive d’une fonction composée :![]()
![]()
Dans le cas particulier où la fonction est égale au produit de la dérivée de l’exposant de e par la fonction eu, la primitive est eu à une constante k près. Notons que ça ressemble à l’envers au calcule de la dérivée de la fonction composée. On peut souvent s’arranger par le calcule faire apparaître la dérivée de l’exposant. Nous verrons cela par des exemples.
NB Pour alléger nous avons simplifier l’écriture, sachant que u c’est u(x).
Cas particulier : primitive de ![]()
La dérivée a de ax+b est absente. Si je la fait apparaître, il faut que je l’enlève immédiatement pour ne pas changer la valeur de f(x). et j’obtiens :

La dérivée de l’exposant ax+b est a. Pour que tout fonctionne bien, il faudrait que l’on ait devant la fonction le nombre a : f(x) = aeax+b.
Or on ne l’a pas. Si on le fait apparaître, il faut tout diviser par a ensuite. Voir ci contre.
Calcule du nombre e
Voyons graphiquement comment on peut s’approcher de la fonction exponentielle à partir de sa tangente en 0.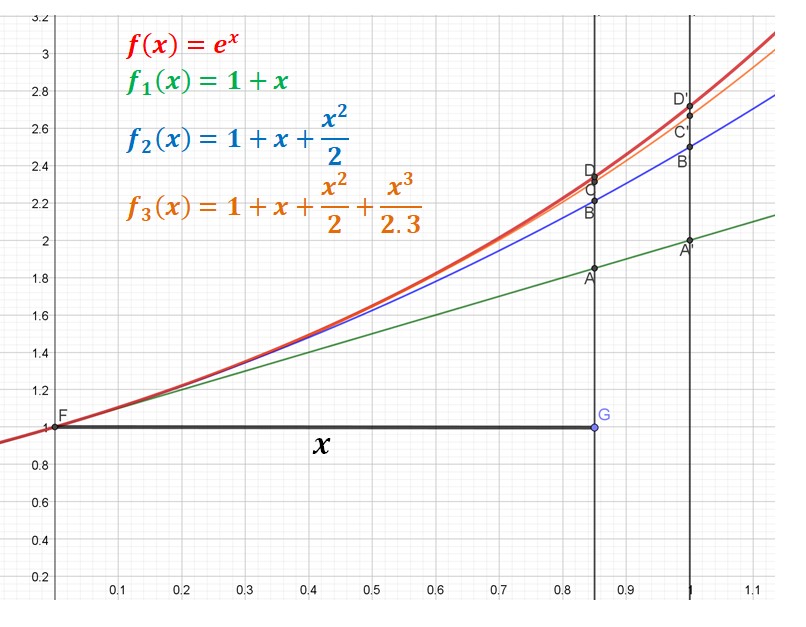


Explications :




Voir ci contre :
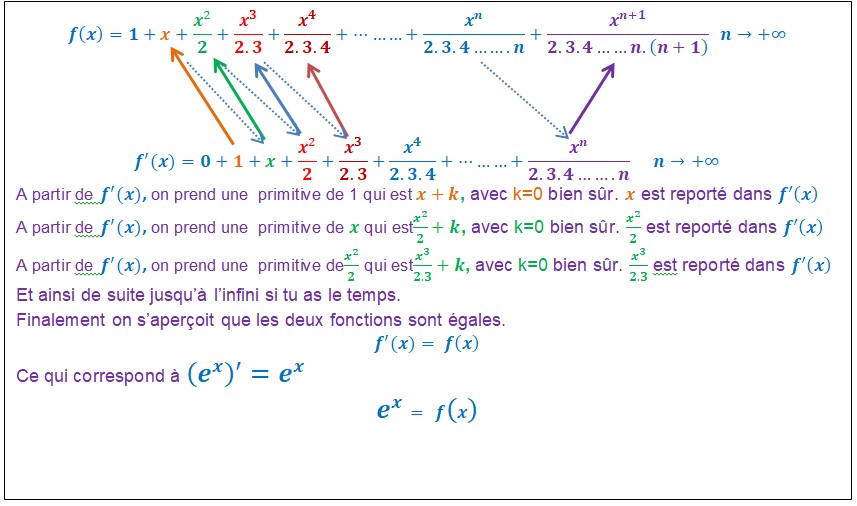
Remarques :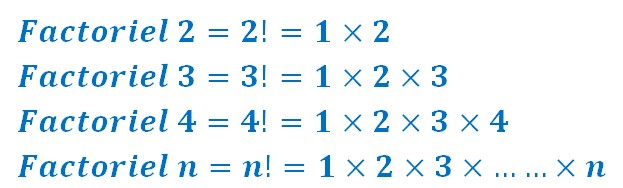
Puisque ![]()
On peut écrire maintenant : 
Le 3ième terme de la formule est![]()
Le dénominateur de la fraction 2 est égal à l’exposant de x. On peut écrire 2 = 1.2
Le 4ième terme de la formule est ![]()
Le dénominateur 2×3 est une multiplication dont le deuxième facteur est égal à l’exposant de x.
Et ainsi de suite :
On appelle factoriel n le nombre suivant :
1 x 2 x 3 x 4 x 5 x……..x n
On peut oublier le 1.
Formule donnant la valeur de e :![]()

Nous en déduisons quelques différentes approximations de la valeur de e :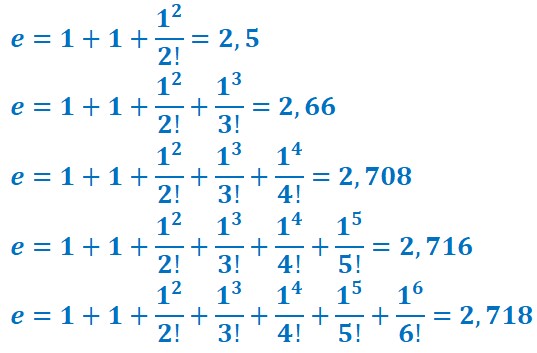
Pour trouver la valeur de e il suffit de remplacer x par 1 dans la formule ci-dessus.
Nous voyons que cette valeur s’affine au fur et à mesure.
En 1748 Euler avait réussi à trouver 18 décimale de e , 2 suivi de 18 chiffres.
En 1853 on avait 137 décimales
En 1949, 2 010
En 1961, 100 265
En 1994, 10 000 000
En 2019 1 000 000 000 000
Nombres complexes
Valeur de ex
autre expression de cette valeur :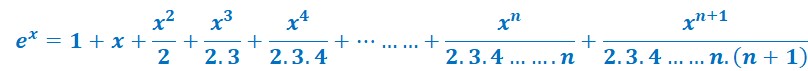
Valeur avec 2n et 2n+1 :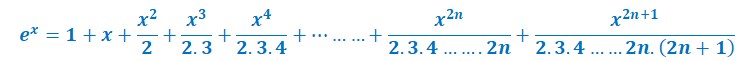
Nous connaissons la valeur développée de ex. On écrire cette valeur en rajoutant un terme n+1 à la fin.
ainsi si on suppose que l’avant dernier terme possède un exposant pair, l’exposant du dernier terme sera obligatoirement impair.
Mais pour qu’il n’y ait pas d’équivoque, on sait que 2n est pair et que 2n+1 est impair.
On peut donc écrire.
Valeur de eiθ :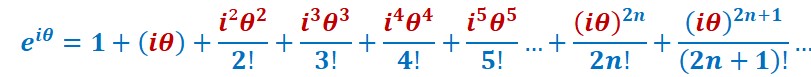
Différentes puissances de i 


Ce qui donne :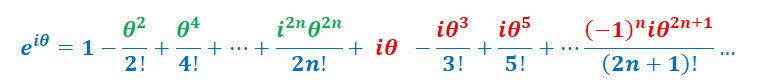 Factorisation par i :
Factorisation par i :
Développement de cosinus et de sinus : 
on en déduit : ![]()
Calculons maintenant eiθ.
Remplaçons x par iθ
Calculons les valeurs des différentes puissances de i
On remplace toutes les puissances de i par leur valeur.
Calculons les puissances de i en fonction de n.
On remplace, puis on factorise par i.
On connaît les développements de cosinus et de sinus. On remarque qu’ils apparaissent dans notre formule. On remplace.
On obtient ainsi la formule donnant l’égalité entre l’expression exponentielle et l’expression trigonométrique d’un nombre complexe.