Théorème de Pythagore
- par gabriel
- dans Géométrie plane, Mathématiques
- sur 15 mai 2020

Le théorème de Pythagore ne s’applique qu’aux triangles rectangles.
Rappel : un triangle rectangle est un triangle qui possède un angle droit.
Les éléments d'un triangle rectangle
Triangle rectangle en A
Pour appliquer le théorème de Pythagore, il est nécessaire de bien repérer l’hypoténuse.
L’hypoténuse est le côté opposé à l’angle droit.
C’est le plus grand côté. Mais parfois il est difficile de discerner le plus grand côté.
Il est préférable pour être sûr de ne pas se tromper de repérer l’angle droit, ce qui est facile en générale et d’en déduire l’hypoténuse qui est juste en face.
Pour la suite et notamment pour la trigonométrie, il est important de repérer les deux autres côtés et de les appeler par leur nom.
Le théorème
Théorème directe :
Si un triangle est rectangle , le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés.
si un triangle est rectangle alors : 
![]()
![]()
Il est également important de connaître l’énoncé du théorème de Pythagore en français faute de le savoir en grec.
En adaptant cette définition au triangle considéré, ici, le triangle ABC , on obtient la formule ci contre.
Bien sûr on adapte l’écriture de cette formule au triangle considéré.
Pour un triangle EFG rectangle en G :
EF²=GE²+GF²
Autre notation
Autre notation d’un triangle : 
![]()
Il existe une autre façon de dénommer un triangle.
On désigne par a le côté BC opposé à l’angle A
On désigne par b le côté AC opposé à l’angle B
On désigne par c le côté AB opposé à l’angle C
Ainsi l’écriture de la formule du théorème de Pythagore change-t-elle et devient : (voir ci contre)
Grâce au théorème de Pythagore, si on connaît dans un triangle la longueur de deux côtés, on peut calculer le troisième côté. Voyons avec quelques exemples.
Exemples
Soit le triangle rectangle ci-dessous :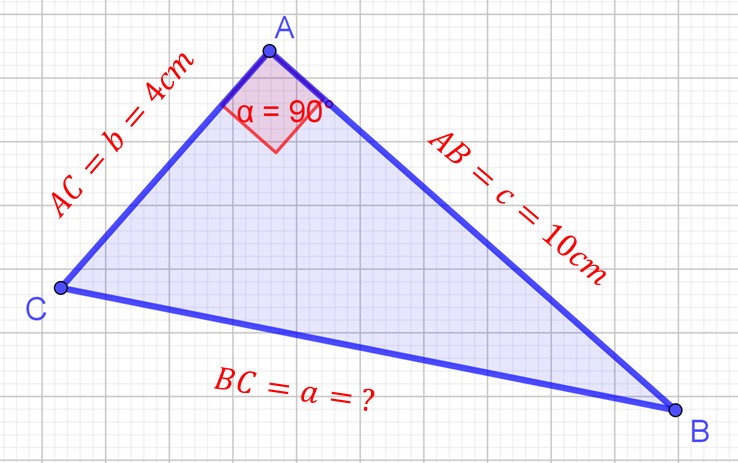
![]()
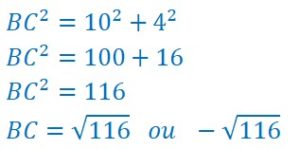
![]()
![]()
Remarque : Il est difficile dans ce triangle de distinguer le plus grand côté. On repère l’angle droit A et on trouve ainsi l’hypoténuse BC.
On peut écrire ![]()
ou ![]()
Comme on cherche BC, il suffit de remplacer AB et AC par leur valeur dans le second membre et de continuer les calculs. 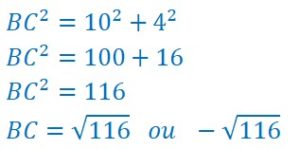
En effet, il existe deux nombres dont le carré est 116. Mais comme il s’agit de longueurs qui ne peuvent être que positives, on garde uniquement la première solution. On obtient la valeur exacte en gardant le radical. On a intérêt à garder cette valeur exacte si on doit faire d’autres calculs avec.
La valeur approchée est donnée par la calculatrice, valeur que l’on arrondira suivant ce qu’on nous demande.
Autre exemple
Je connais l’hypoténuse et un côté de l’angle droit, il s’agit de trouver l’autre côté. 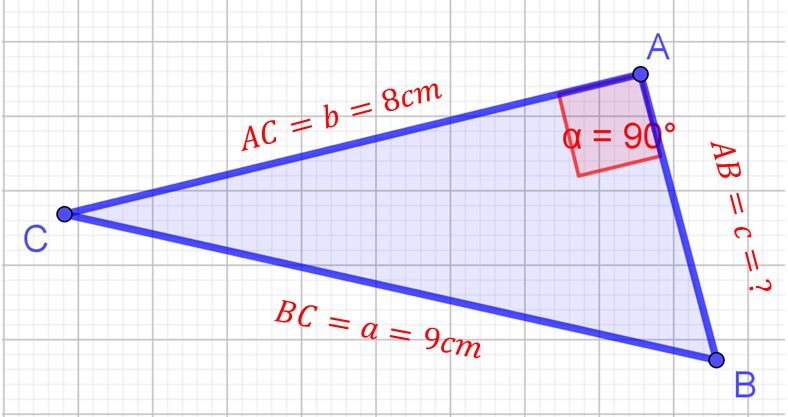
![]()
![]()
![]()
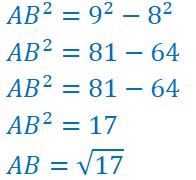
![]()
Ou bien :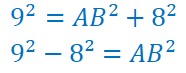
……..
Avant toute chose on écrit la formule du théorème de Pythagore telle qu’on l’a apprise avec le carré de l’hypoténuse dans le premier membre. Ceci, afin, de ne pas faire d’erreur.![]()
Première manière élégante :
Comme on doit calculer AB, j’isole AB dans le second membre où il se trouve et je fais passer AC dans le premier membre en changeant son signe. C’est une équation. ![]()
Pour les fanatiques du premier membre, ceux qui veulent toujours les inconnues dans le premier membre, on rétabli : ![]()
Ensuite ce ne sont que des calculs : 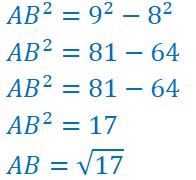
Je n’oublie pas que deux solutions se présentent à cette équation mais puisqu’on est en géométrie, on ne retient que la solution positive.
Avec la calculatrice on trouve une valeur approchée qu’on arrondira selon les besoins. ![]()
Autre méthode plus prosaïque :
Une fois la formule écrite on remplace tout de suite par les valeurs connues.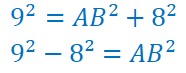
Ensuite ce ne sont que des calculs.
Réciproque
Si dans un triangle, le carré du côté le plus long est égal à la somme des carrés des deux autres côtés, le triangle est rectangle. ![]()
![]()
Bien saisir la différence entre théorème directe et réciproque.
Pour le théorème directe, on part du fait connu que le triangle est un triangle rectangle et on en conclue la relation entre les carrés des côtés.
Pour la réciproque on part d’un triangle qui satisfait la relation entre les carrés des côtés et on aboutit à la conclusion que le triangle est rectangle.
On peut écrire le théorème directe et la réciproque en une seule formule ci-contre hypothèse et conclusion étant séparées par une double flèche en bleue qui permet de lire l’assertion dans les deux sens.
Exemple
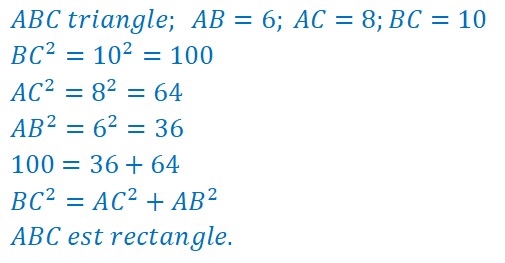
Un triangle ABC dont les côtés mesurent AB=6 cm, AC=8 cm et BC=10 cm est-il un triangle rectangle ?
On calcule le carré du plus grand côté BC²=10²=100
On calcule le carré de l’un des deux autres côtés AC²=8²=64
On calcule le carré du dernier côté AB²=6²=36
Et on remarque que 100=36+64
soit BC²=AB²+AC²
Le triangle est rectangle.
Contraposée
Si dans un triangle le carré du plus grand côté n’est pas égal à la somme des carrés des deux autres côtés, le triangle n’est pas rectangle.
![]()
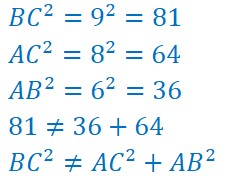
D’après la contraposée du théorème de Pythagore : ![]()
Remarque : souvent, on peut se passer du schéma du triangle. Mais si ça aide, il ne faut pas s’en priver.
Un triangle ABC dont les côtés mesurent AB=6 cm, AC=8 cm et BC=9 cm est-il un triangle rectangle ?
On calcule le carré du plus grand côté BC²=9²=81
On calcule le carré de l’un des deux autres côtés AC²=8²=64
On calcule le carré du dernier côté AB²=6²=36
Et on remarque que 81≠36+64
soit BC²≠AB²+AC²
La réciproque ne nous rien sur cette éventualité.
Il nous faut trouver une autre assertion. Voir ci-contre.
C’est la contraposée du théorème de Pythagore.
C’est la négation de la réciproque.