Equations à une inconnue
- par gabriel
- dans Equations inéquations, Mathématiques
- sur 17 mai 2020

Sommaire :
Les deux premiers chapitres permettent de comprendre la logique d’une équation. Il ne faut pas prendre en considération la méthode de résolution exposée ici. Il est inutile de s’entraîner avec cette méthode.
Très rapidement, il faut aboutir à résoudre les équations selon la méthode exposée dans le chapitre « 3-Résolution pratique » qui est la seule rapide et efficace et qui servira tout au long de la scolarité, de la quatrième à l’enseignement supérieur.
Balance
Pour peser un objet, on utilisait autrefois une balance à plateaux. Aujourd’hui, les balances sont automatique et électroniques. Dès qu’on pose l’objet sur un plateau, un écran nous indique son poids.
Avant on posait l’objet sur un plateau et sur l’autre on ajoutait des poids marqués jusqu’à obtenir l’équilibre : les 2 plateaux bleus au même niveau et la flèche rouge au milieu.

Sur le plateau de droite j’ai mis 7 bonbons.
Sur le plateau de gauche, j’ai mis 2 poids de 10 g et 3 poids de 5 g. Ce qui fait 35 g en tout.
La balance étant en équilibre, j’en déduis que mes 7 bonbons ont une masse de 35 g.
ATTENTION : Dans la vie quotidienne, on parle de poids : le poids des bonbons est de 35 g. Mais en physique il s’agit de masse. Le poids étant différent de la masse. La masse est la quantité de matière.
Dans notre cas le poids des bonbons serait environ de 350 Newton.
Il fat donc toujours lorsqu’on pèse quelque chose parler de masse. En plus le verbe peser qui vient de poids est impropre. Il faudrait dire masser, mais c’est autre chose !
Si j’enlève 2 bonbons par exemple 
Le plateau droit qui possède une masse moins importante va s’élever, alors que le plateau gauche qui possède une masse plus importante s’abaisse et que la flèche rouge du milieu penche vers la gauche.
Pour équilibrer la balance à nouveau, soit on rajoute les bonbons là où ils étaient, soit on enlève deux poids (on devrait dire masses) de 5 g. 
Maintenant on a équilibré la balance avec une série de poids de chaque côté, sur chacun des plateaux. 
Si j’enlève une masse de 10 g sur le plateau droit, la balance est déséquilibrée. 
Pour l’équilibrer à nouveau je dois enlever la même masse de 10 g du plateau gauche.
Equation = balance
Une équation, c’est comme une balance. En plus elle doit toujours être équilibrée.
Une équation est constituée de deux membres séparés par le signe égal. 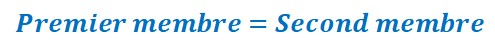
En fait c’est une égalité dans laquelle on a une inconnue. Pour que cette égalité soit toujours vraie, il faut opérer comme sur la balance. Si j’enlève quelque chose dans le second membre, je dois enlever la même chose dans le premier membre. Et vice versa.
Le but est de résoudre l’équation, c’est-à-dire trouver la valeur de l’inconnue.
Par exemple, soit l’équation : ![]()
Cela signifie qu’on cherche une valeur x qu’on ne connaît pas (on pourrait l’appeler y ou a ou tartampion) telle que deux fois cette valeur plus 5 soit égale à cette valeur plus 6.
On doit arriver à la fin à une égalité du genre :![]()
Voyons comment procéder.
Premier exemple![]()
Je dois faire en sorte d’obtenir toutes les inconnues, les x dans un membre et les nombre connus dans l’autre.
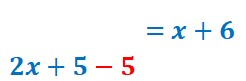
Je vais isoler par exemple les x dans le premier membre (on pourrait choisir le second membre, c’est selon la simplicité de l’opération); Pour cela je dois enlever le 5 dans le premier membre.
Comme pour la balance, mon équation est déséquilibrée.
![]()
![]()
Il faut vite que j’enlève 5 au second membre pour la rééquilibrer.
J’effectue les calculs pour simplifier.
![]()
Je dois me débarrasser de ce x tout seul dans le second membre. Mais en même temps, je dois enlever un x dans le premier membre pour garder l’équilibre de l’équation.
![]()
En calculant dans chacun des membres, je trouve la réponse.
Second exemple ![]()
Je procède de la même manière, mais attention, il existe des nombres négatifs.
![]()
![]()
![]()
J’ai -3x dans le deuxième membre. Pour l’éliminer, je rajoute 3x dans ce second membre.
Pour garder l’équilibre de l’équation, je rajoute 3x aussi dans le premier membre.
Je réduis, je calcule dans les deux membres.
![]()
![]()
Dans le premier membre, pour isoler les 7x, je dois enlever le +5 en le soustrayant.
Je réduis et calcule dans les deux membres.
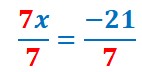
![]()
J’aborde une étape supplémentaire.
Dans le premier membre, il faudrait que j’aie x tout seul, or j’en ai 7 fois plus : 7x.
Pour en avoir un seul, je dois diviser le premier membre par 7. Mais pour conserver l’équilibre de l’équation, je dois diviser aussi le second membre par 7.
Ce qui me donne en simplifiant les deux membres :
Cette méthode de résolution d’une équation, fastidieuse, est élaborée pour comprendre le mécanisme d’une équation. Mais il faut abandonner très vite cette méthode pour en utiliser une beaucoup plus simple et plus rapide.
On s’aperçoit en réfléchissant un peu que additionner ou soustraire un nombre d’un membre pour l’annuler et faire la même chose dans l’autre membre, revient après réduction à déplacer ce nombre d’un membre à l’autre en changeant son signe.
Résolution pratique
Règles fondamentales :
On peut additionner ou soustraire un même nombre ou une expression des deux membres d’une équations.
Ce qui revient dans la pratique à :
Dans une équation, on peut changer un nombre ou une expression de membre à condition de changer son signe.
On peut multiplier ou diviser les deux membres d’une équation par un même nombre ou expression.
![]()

J’isole les inconnues (les x) dans le premier membre et les nombres connus dans le second.
Je fais passer 3x dans le premier membre en changeant son signe.
Je fais passer +3 dans le second membre en changeant son signe.
![]()
J’obtiens une nouvelle équation :
![]()
Je réduis les deux membres.
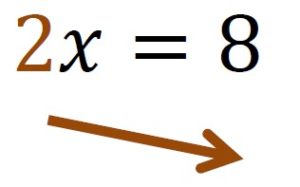
Je divise les deux membres par 2.
ce qui revient à faire passer le 2 dans le second membre mais à l’étage en dessous, comme dénominateur.

![]()
J’obtiens la valeur de x que je peux éventuellement simplifier.
En résumé :
J’isole les inconnues dans un membre et les nombre connus dans l’autre.
Lorsque je fais passer un nombre ou une expression d’un membre à l’autre, je change son signe.
SI les nombres ne sont pas très compliqués, tout cela se fait de tête.
On peut isoler les inconnues soit dans le premier membre, soit dans le second. Personnellement, je les isole dans le membre où ils seront positifs.
On utilise les règles courantes de calculs.
Si les nombres parlaient

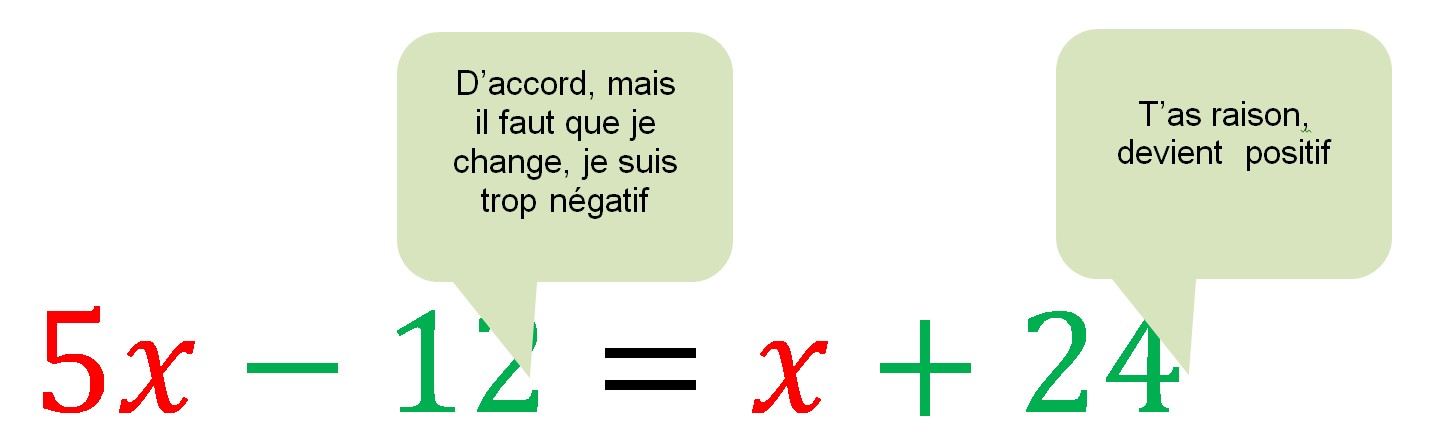
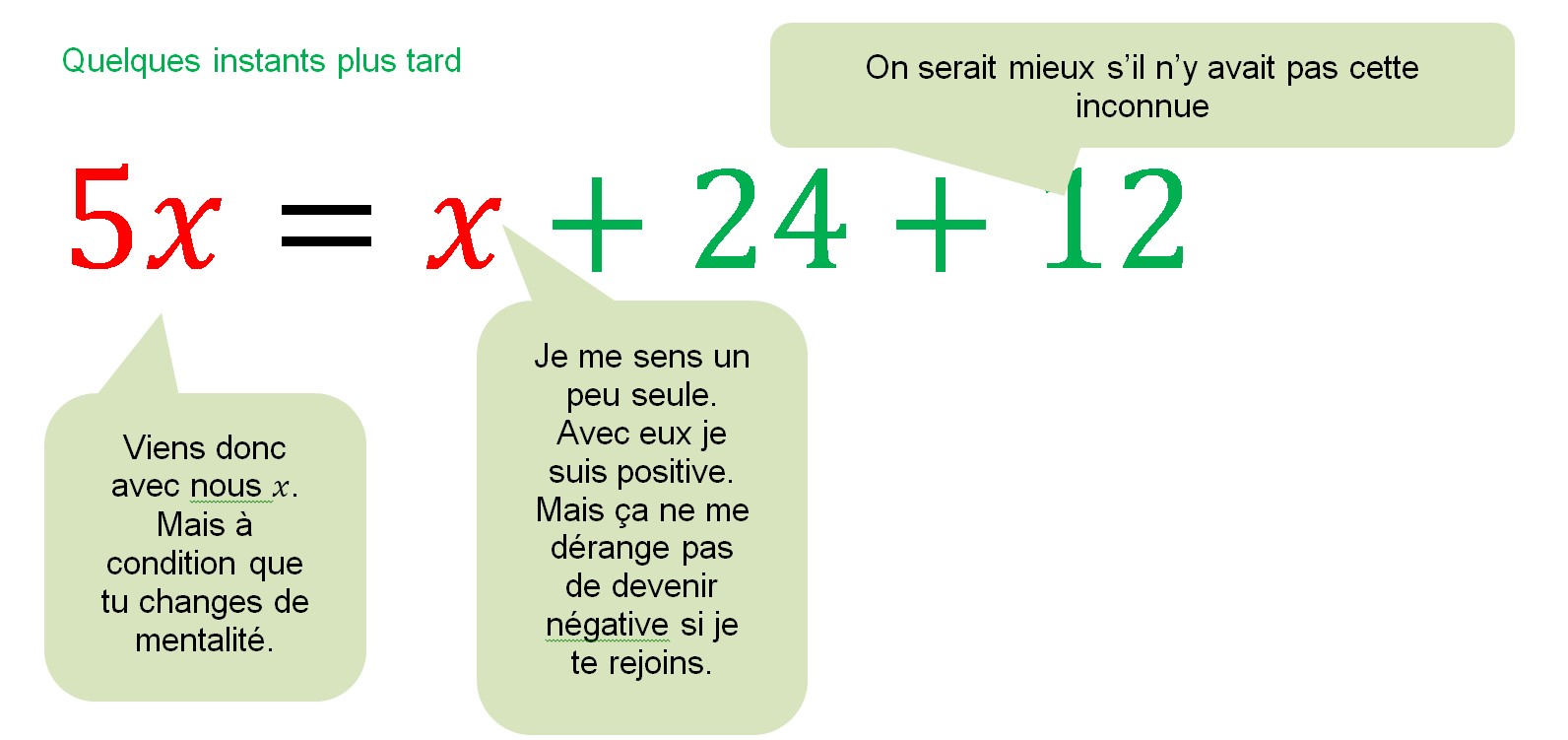

Exemples d'équations



Au niveau du développement, je mets l’inconnue avant la racine, pour éviter toute confusion : x ne doit pas être sous le radical.
Pour rendre le dénominateur rationnel (sans radical) il faut multiplier le dénominateur par sa quantité conjuguée pour obtenir la troisième identité remarquable qui une fois développée élimine les radicaux. Bien sûr, on doit aussi multiplier le numérateur par cette même quantité conjuguée pour ne pas changer la valeur de la fraction.
La valeur de x est irrationnelle, elle ne peut pas se réduire à une fraction simple. Mais son dénominateur, lui est rationnel.
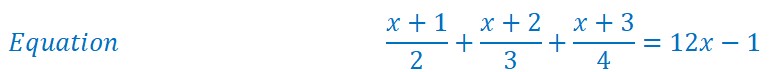
Une série d’addition de fraction est égale à un nombre composé (finalement une fraction qui a 1 pour dénominateur).
Je pourrais réduire uniquement le premier membre au même dénominateur. Mais pour montrer une autre technique, je réduis les deux membres au même dénominateur 12.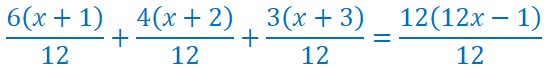
Je peux écrire en multipliant les deux membres par 12 :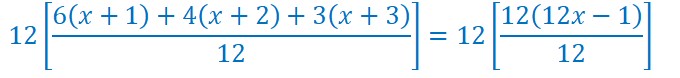
Je simplifie les deux membres par 12.
Les dénominateurs disparaissent, mais je n’ai pas le droit de dire, comme le font nombre d’enfants, que je supprime les dénominateurs. ![]()
Je développe, j’isole les inconnues dans le deuxième membre (pourquoi pas ? Dans ce cas c’est plus pratique), je réduis et trouve le résultat : 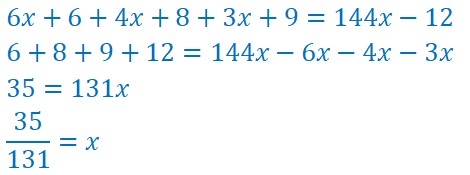
Je vérifie : 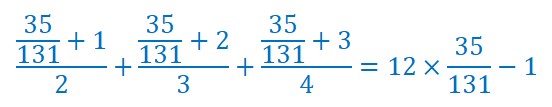
Equations en vidéo
Equations avec fractions
https://youtu.be/bJ2cOy4HBtc