Diviseurs
- par gabriel
- dans arithmétique, Mathématiques, Non classé
- sur 13 juin 2025
Vocabulaire
Définition d'un diviseur


Avec un exemple pour comprendre plus facilement 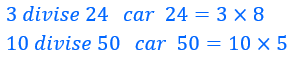
La définition ci-contre se fait à partir de la multiplication car on n’est pas censé connaître encore la division.
La définition est valable aussi pour les entiers relatifs.
Autre manière de le dire

En prenant l’exemple ci-dessus :
3 divise 24
3 est diviseur de 24
car si on divise 24 par 3 on obtient un nombre entier non nul, 8
On peut dire aussi que
24 est un multiple de 3 ou que 24 est divisible par 3.
Attention de ne pas mélanger toutes ces expressions qui signifient la même chose différemment.
le dire en langage mathématique.
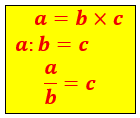
![]()
C’est la première définition du diviseur. ![]()
en utilisant la division, il est plus évident que 3 divise 24 ou que 3 est diviseur de 24.
De même en utilisant une fraction.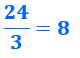
Les critères de divisibilité.
Comment savoir si un nombre est divisible par un autre nombre sans faire la division même si avec la calculatrice il est très facile d’effectuer cette opération.

2458 se termine par 8 qui est un chiffre pair
2458 est divisible par 2. 2458:2=1229
2457 se termine par 7 qui n’ est pas un chiffre pair
2457 n’ est pas divisible par 2. 2457:2=1228,5

2451 2+4+5+1=12 2+1=3
la somme de ses chiffres est un multiple de 3
2451 est divisible par 3. 2451:3=817
2452 2+4+5+2=13 3+1=4
La somme de ses chiffres n’ est pas un multiple de 3
2452 n’ est pas divisible par 3 2452:3=817,3333

2496 96:4=24
le nombre formé par les deux derniers chiffres est un multiple de 4
4 2496 est divisible par 4 2496:4=624
2445 45:4=11,25
Le nombre formé par les deux derniers chiffres n’ est pas un multiple de 4
2445 n’ est pas divisible par 4 2445:4=611,25

2495 se termine par 5; il est divisible par 5 ; 2495:5=499
2490 se termine par 0 ;il est divisible par 5; 2490:5=498
2446 ne se termine pas par 0 ou 5 ; il n’ est pas divisible par 5; 2446:5=489,2

2484 se termine par un nombre pair, il est divisible par 2
2484 2+4+8+4=18 1+8=9
la somme de ses chiffres est un multiple de 3, il est divisible par 3
2484 est divisible par 2 et par 3 donc par 6,2484:6=414
2485 ne se termine pas par un nombre pair, il n’ est pas divisible par 2
2485 n’ est pas divisible par 6, 2485:6=414,16666

Pour la divisibilité par 7 c’est compliqué et il est préférable de vérifier avec la calculatrice la divisibilité du nombre par 7. A titre d’exemple cependant :
5488 548 dizaines 548+5×8=548+40=588
588 58 dizaines 58+5×8=58+40=98
98 9 dizaines 9+5×8=49
49 est multiple de 7 donc 5488 est divisible par 7
On ne donner pas de contre exemple .

13104 on divise par 2 le nombre formé par les 3 derniers chiffres
104:2=52 on divise encore par 2 le résultat
52:2=26 on divise encore par 2 le résultat
26:2=13
104 est donc divisible 3 fois par 2, 13104 est divisible par 8
On ne donnera pas de contre exemple.

2484 2+4+8+4=18 1+8=9
la somme de ses chiffres est un multiple de 9,il est divisible par 9
2484:9 = 276
2485 2+4+8+5=19 1+9=10
La somme de ses chiffres n’ est pas un multiple de 9,
il n’ est pas divisible par 9 2485:9=276,1111

2400 se termine par 0, il est divisible par 10 2400:10 = 240
2405 ne se termine pas par 0, il n’est pas divisible par 10 2405:10 = 240,5
Les nombres premiers
 5:1=5
5:1=5
5:2=2,5 2 n’ est pas un diviseur de 5
5:3=1.666 3 n’ est pas un diviseur de 5
5:4=1,25 4 n’ est pas diviseur de 5
5:5=1
5 est un nombre premier
Il existe une infinité de nombres premiers.
Tout nombre n possède au moins deux diviseurs : 1 et lui même, n.
Il existe des nombres qui ne possèdent que deux diviseurs et seulement deux, ce sont les nombres premiers.
Les nombres premiers ne peuvent être divisés que par 1 et par eux même .
Si on divise un nombre par 1 on obtient le nombre comme résultat.
Si on divise un nombre par lui même, on obtient 1 comme résultat.
Liste des nombres premiers.
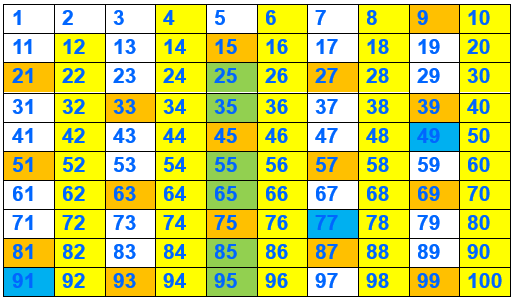
On colore en jaune tous les multiples de 2
On colore en orange les multiples de 3 qui restent
Les multiples de 4 on déjà été éliminés par les multiples de 2
On colore en vert les multiples de 5 qui restent
Les multiples de 6 ont été éliminés (multiples de 3 et de 2)
On colore en bleu les multiples de 7 qui restent.
Les multiples de 8 ont déjà été éliminés comme multiples de 2
Les multiples de 9 ont été éliminés comme multiples de 3
Enfin les multiples de 10 ont été éliminés comme multiples de 2
Bien que les mathématiciens s’y penche depuis la nuit des temps, il n’existe pour l’instant aucune formule, aucune méthode qui permette de trouver la liste des nombres premiers. La seule manière de savoir si un nombre est premier est de tester en le divisant tour à tour par tous les nombres en partant de 2
On peut aussi recopier tous les nombres dans un tableau et barrer successivement ceux qui sont divisibles par 2, puis barrer ceux qui sont divisibles par 3…. A la fin on obtient une liste de nombre premier. Cette méthode se nomme la crible d’Eratosthène.
Ci-contre, un exemple pour les nombres inférieurs à 25.
Comment reconnaître si un nombre est premier.
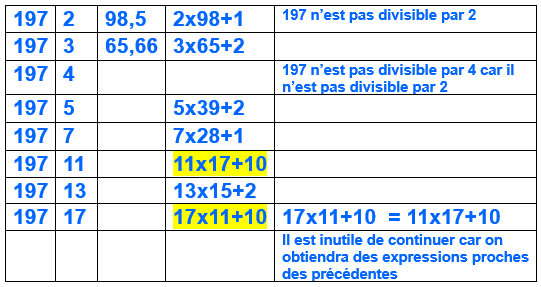

197 est-il un nombre premier ?
Il suffit de vérifier si le nombre en question, 197, est divisible par chacun des nombres premiers, 2,3,5,7,11,13,17,19,23,29,…
Le processus pourrait être long voire infini.
Mais on remarque qu’à partir d’une certaine valeur on retrouve les mêmes opérations ou des opérations dont les résultats sont très proches.
Décomposition d'un nombre en produit de facteurs premiers


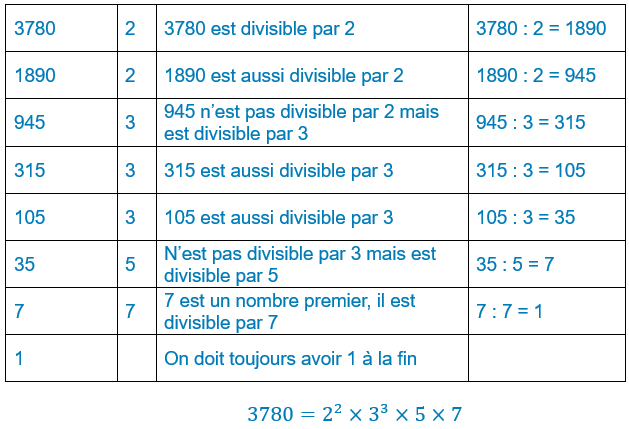
On construit un tableau comme ci-contre mais ne contenant que les deux premières colonnes. Les autres colonnes ne servant qu’à expliquer les démarches à suivre.
On cherche si chacun des nombres de la première colonne est divisible successivement par les nombres premiers, d’abord 2, puis 3, puis 5..
On respecte l’ordre pour ne pas en oublier.
On obtient ainsi une succession de nombres premiers dont le produit est la décomposition du nombre facteurs de nombres premiers.
Cette décomposition est valable pour les petits nombres mais devient fastidieuse pour les grands nombres. Dans ce cas, on peut utiliser d’autres procédures qui seront éventuellement toutes différentes en fonction du nombre dont on veut faire la décomposition.
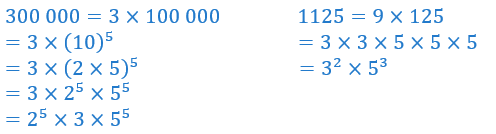
Ci-contre deux exemples de décompositions en produits de facteurs premiers sans utiliser la première méthode.
On pet bien sûr utiliser la calculatrice afin que le travail soit le moins fastidieux possible et permette de libérer notre cerveau pour des raisonnements plus compliqués.
Les diviseurs d'un nombre

Un nombre quelconque possède un nombre limité de diviseurs.
Le plus grand diviseur que peut posséder un nombre est lui même.
Autrement dit un nombre ne peut pas posséder un diviseur plus grand que lui, puisque le résultat de la division de ce nombre par un nombre plus grand que lui est obligatoirement un nombre décimal plus petit que zéro.
Le plus petit diviseur que peut posséder un nombre quelconque est 1 puisque les diviseurs appartiennent à l’ensemble des entiers naturels sachant que la division par 0 n’a pas de sens mathématique (on ne peut pas faire un partage entre 0 personnes)
Propriétés des diviseurs d'un nombre
Nous avons vu la notion de diviseurs d’entiers naturels. Elle peut être étendue à l’ensemble des entiers relatifs.







Trouver tous les diviseurs d'un nombre n
Première méthode
On effectue successivement toutes les divisions du nombre n par tous les nombres de 1 jusqu’à n.
C’est la méthode la plus simple, celle qui vient immédiatement à l’esprit. Mais comme elle est fastidieuse !
Et pour les grands nombres…
Remarquons que si un nombre n est divisible par p.
On aura n=pq. Donc q est aussi diviseur de n.
On n’est donc pas obligé de chercher les diviseurs avec tous les nombres de 1 jusqu’à n. Il suffit de s’arrêter lorsqu’on dépasse la racine de n.

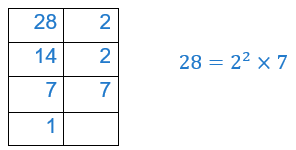
Qu’on prenne tous les nombres de 1 à 28 ou bien qu’on s’arrête lorsqu’on dépasse la racine carrée de 28, on trouve tous les diviseurs de 28, à savoir :1,2,4,7,14,28.
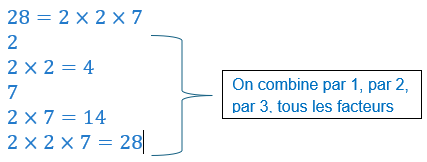
Deuxième méthode
avec la décomposition du nombre n en produits de facteurs premiers.
Lorsqu’on a effectuer la décomposition du nombre n en produits de facteurs premiers on peut trouver tous les diviseurs en effectuant les produits de toutes les combinaisons possibles des différents facteurs.
C’est moins fastidieux, mais on risque d’oublier des diviseurs.
Troisième méthode
On élabore un arbre à partir de la décomposition en produits de facteurs premiers.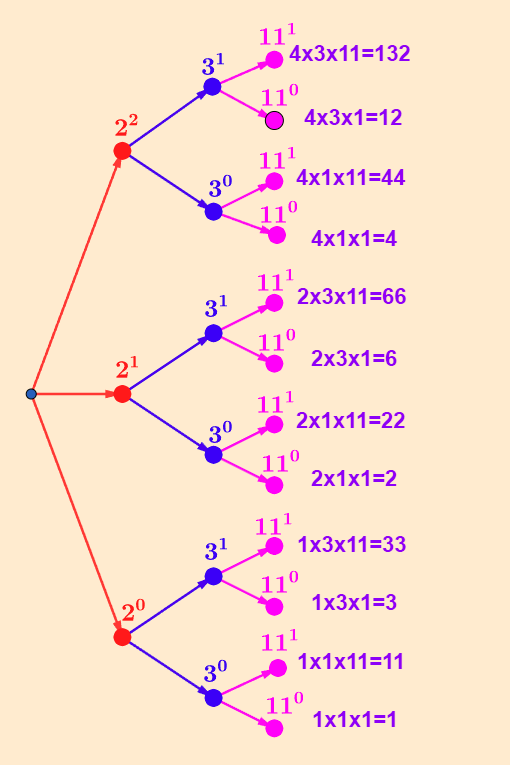
Quels sont tous les diviseurs du nombre 132 ?
On commence par décomposer ce nombre en produit de facteurs premiers :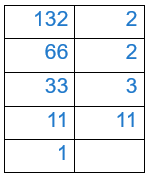
![]()
On obtient 3 facteurs.
Prenons le facteur 2. IL est élevé à la puissance 2. Cela signifie que 2 et 22, ou 21 et 22 ou encore 2 et 4 sont diviseurs de 132. Mais le facteur 1 n’apparaît jamais dans la décomposition. Pourtant c’est un diviseur de 132. Il n’apparaît pas car 1 est un élément neutre de la multiplications. Nous savons d’autre part que 20=1 (tout nombre élevé à la puissance 0 est égal à 1)
Nous pouvons donc écrire que les diviseurs de 132 dont le facteur est 2 sont : 20,21,22. On procède de la même manière pour les facteurs 3 et 11.
A partir de là, nous pouvons construire un arbre ayant 3 niveaux. Avec cet arbre on peut calculer les diviseur en suivant chacune de ses ramifications.
Voir l’arbre ci-contre.
Ainsi nous voyons que les diviseurs de 132 sont dans le désordre et en commençant par la ramification du bas :
1,11,3,33,2,22,6,66,4,44,12,132
Ou en les ordonnant :
1,2,3,4,6,11,12,22,33,44,66,132
Et on est certain avec cette méthode d’obtenir absolument tous les diviseurs de 132.

Appliquons cette méthode au nombre 132![]()
Les 3 facteurs donneront
Les diviseurs seront donc :
Nombre de diviseurs d'un entier

Prenons l’exemple du nombre 132 précédent dont la décomposition en produit de facteurs premiers est : ![]()
le premier facteur est 2, sont exposant est 2 auquel on ajoute 1 (2+1).
le deuxième facteur est 3, son exposant est 1auquel on ajoute 1 (1+1).
le troisième exposant est 11, son exposant est 1 auquel on ajoute 1 (1+1)
Ainsi le nombre de diviseurs de 132 sera :
(2+1)(1+1)(1+1)=3 x 2 x 2 = 12
Dans les techniques précédentes pour chercher tous les diviseurs de 132, on en a bien trouvé 12. Rappel 1 et le nombre lui même sont diviseurs de ce nombre.
Plus grand diviseur commun : PGCD
Diviseurs communs à deux nombres
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
Deux nombres entiers différents peuvent éventuellement avoir plusieurs diviseurs communs.
Dans l’exemple ci-contre 450 et 140 ont trois diviseurs en commun : 1;2 et 10.
Si deux nombres ne possèdent aucun diviseur commun à part le chiffre 1, ils sont premiers entre eux.
Une condition nécessaire et suffisante pour qu’un nombre p soit divisible par un nombre q est que le nombre p contienne chaque facteur du nombre q avec des exposants au moins égaux
450 n’est pas divisible par 140 car 450 ne possède pas tous les facteurs de 140
Notations

Prenons deux nombres : 450 et 140.
Cherchons tous les diviseurs de 450 et de 140.
Pour cela on décompose les deux nombres en produit de facteurs premiers. 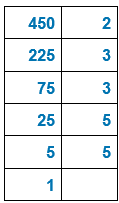
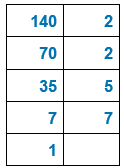
![]()
![]()
Avec une des méthodes ci-dessus ou avec un logiciel, cherchons tous les diviseurs de chacun des deux nombres.
450 possède (1+1)(2+1)(2+1)=2 x 3 x 3 = 18 diviseurs qui sont :![]()
140 possède (2+1)(1+1)(1+1) = 3 x 2 x 2 =12 diviseurs qui sont :![]()
On s’aperçoit que les deux nombres 450 et 140 ont trois diviseurs en commun , 1;2 et 10.
Le plus grand de ces divisuers communs est 10.
C’est le PGCD des nombres 450 et 140.
Différentes méthodes de calcul du PGCD
Méthode des diviseurs
Trouver tous les diviseurs de a, les ordonner.
Trouver tous les diviseurs de b, les ordonner.
Repérer tous les diviseurs communs à a et b
Prendre le plus grand qui sera bien sûr le PGCD
Quel est le PGCD des nombres 15 et 18![]() Les diviseurs de 15 sont 1, 3, 5, 15
Les diviseurs de 15 sont 1, 3, 5, 15![]() Les diviseurs de 26 sont 1, 2, 3, 6,18
Les diviseurs de 26 sont 1, 2, 3, 6,18![]() Les diviseurs communs à 15 et 26 sont 1, 3
Les diviseurs communs à 15 et 26 sont 1, 3![]() Le plus grand est 3
Le plus grand est 3
Le PGCD de 15 et 18 est donc 3
Méthode par la décomposition en produits de facteurs premiers
Méthode des soustractions

A partir de cette propriété on effectue des soustractions successives.
Le PGCD est le dernier résultat trouvé autre que 0
Quel est le PGCD des nombres 96 et 36
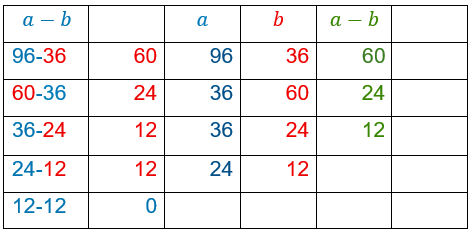
Le PGCD de 96 et 36 est 12
Méthode par l'algorithme d'Euclide
 A partir de cette propriété on effectue des divisions successives, le dernier rets non nul estle PGCD
A partir de cette propriété on effectue des divisions successives, le dernier rets non nul estle PGCD
