Les angles
Qu'est-ce qu'un angle ?
Une île au milieu de la mer. La nuit tombe lentement.
Le phare va bientôt commencer à émettre son rayon laser pour guider les bateaux de pêcheurs qui rentrent après une journée de pêche fructueuse. Les cales sont pleines de poissons qui s’agitent encore à la recherche de l’oxygène dissoute dans l’eau.
Voyons ci-dessous le fonctionnement du phare.
Voici le phare vu de dessus.
le rayon laser OA est immobile.
En cliquant sur le bouton “Initialiser/Démarrer” le rayon OB se met à tourner. Il s’écarte de sa position initiale OA. Cet écart correspond à un angle dessiné en hachures rouges.
En cliquant sur la petite flèche pause, l’animation s’arrête. On observe la position OB du faisceau laser, ainsi que sa position initiale OA.
Le rayon laser OB s’est écarté de OA.
Cet écart correspond à un angle que l’on mesure en degré.
Tu remarques la mesure de l’angle indiquée à côté de la hachure rouge.
Définition
la portion du plan colorié en rouge est un angle.
Cet angle est délimité par deux demi-droites d et d’ qui se coupent en O.
Bien sûr nous n’avons pu représenter qu’une portion de l’angle.
En effet les demi-droites d et d’ vont jusqu’à l’infini à partir de O.
ainsi l’angle en rouge continue jusqu’à l’infini.
On remarque qu’à mesure on s’éloigne du point O, les deux droites s’écartent de plus en plus.
Exemples d'angles
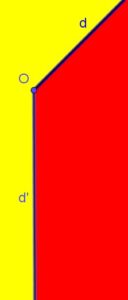
Tous ces angles ont un sommet O et sont délimités par deux demi-droites d et d’. Chaque angle est colorié en rouge.
Une unité de mesure des angles : le degré.
Dans un cercle, il y a 360 degrés.
Imagine que dans l’animation ci-contre le cercle soit une tarte qu’on doit partager entre 360 personnes.
Imagine que le segment OB soit un couteau qui coupe cette tarte en portions de un degré à mesure qu’il avance.
n représente le nombre de portions qu’il vient de couper.
A la fin, il a coupé toutes les portions et tu peux remarquer que ta tarte possède 360 portions (n est égal à 359 pour un problème technique, mais on ne va pas chipoter). Ainsi le cercle est divisé en 360 parties de un degré.
Tu peux voir qu’un angle de 1 degré est un très petit angle.
Lorsque tu es en pose. l’angle AOB est divisé en petits angles de un degré.
Le nombre de ces petits angles de un degré est indiqué par le nombre n ce qui correspond à la mesure de l’angle AOB en degrés
Mesure des angles : degrés, minutes, secondes
Angle de un degré.
Angle de soixante minutes
Angle de trois mille six cents secondes 
Ci contre, on a dessiné un angle de un degré.
C’est un très petit angle.
Pour mesurer des angles plus petits que un degré, on pourrait écrire 0 degré virgule 2 par exemple 0,2. Soit deux dixièmes de degré. On divise le degré en 10 et on prend deux parties. Souvent, on fera ainsi.
Mais on peut partager notre angle de un degré en 60 parties au lieu de 10. Chaque partie est appelée une minute d’angle pour ne pas confondre avec la minute du temps.
Notre angle de un degré mesure aussi soixante minutes d’angle.
Ce n’est pas tout. On divise aussi un angle de une minute d’angle en soixante parties. Chaque partie est appelée une seconde d’angle. Un angle de une minute est égal à un angle de soixante seconde.
Un angle de 1 degré est égal à un angle de 60 minutes et aussi à un angle de 3600 secondes (60 x 60).
Nommer un angle
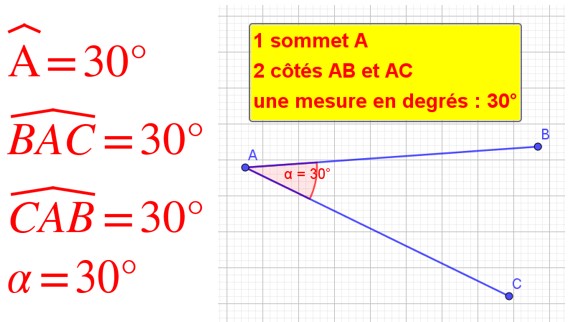
Un angle est constitué d’un sommet (point A) et de deux demi-droites. Sur chacune des demi-droite on peut noter deux points B et C. Ainsi les côtés de l’angle sont désignés par AB et AC correspondant aux deux demi-droites d et d’.
Cet angle peut être désigné par son sommet A en lui mettant un chapeau pour montrer qu’il s’agit d’un angle et non pas du point A.
Il peut être désigné aussi par trois points, ceux constituant les côtés et le sommet. On place le nom du sommet au milieu des deux autres lettres. Le tout avec un chapeau.
On peut aussi le désigner par une lettre grecque, ici alpha.
Angles particuliers
Angle plat
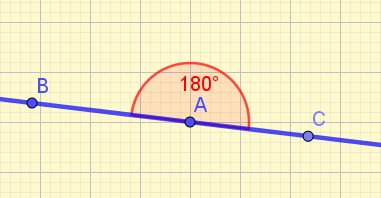
Les trois points BAC sont alignés. On dit qu’il est plat par opposition à un angle pointu.
La mesure d’un angle plat est égale à 180 degrés.
On rappelle qu’un cercle a une mesure de 360 degrés.
Dans un cercle on peut construire deux angles plats délimités par un diamètre. 
Angle droit
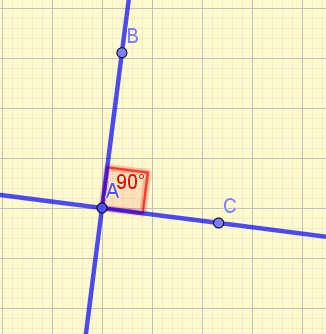
Un angle droit a ses côtés AB et AC perpendiculaires.
C’est la moitié d’un angle plat.
C’est le quart d’un cercle.
Dans un cercle on peut construire quatre angles droits délimités par deux diamètres perpendiculaires.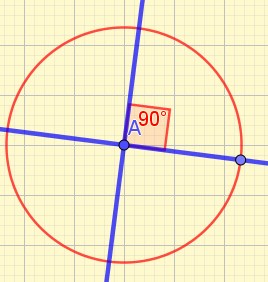 
Angles aigus, obtus, saillants, rentrants
Angle aigu.
L’angle est compris entre 0 et 90 degrés
Angle obtu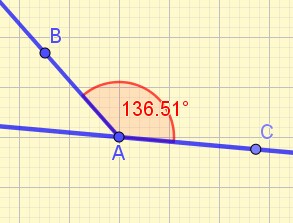
l’angle est compris entre 90 et 180 degrés.
Angle saillant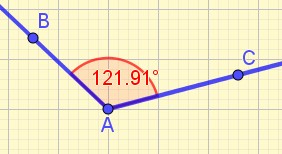 
L’angle est compris entre 0 et 180 degrés. Il peut être aigu, droit ,obtus ou plat.
Angle rentrant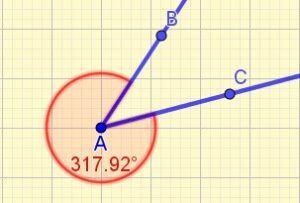
L’angle est plus grand que 180 degrés. On comprend sur le dessin pouquoi on l’appelle rentrant.
Angles égaux
Pour répondre aux deux questions ci-dessus, clique sur le curseur avec la souris et déplace le point vers la droite. Le premier angle se déplace et vient se superposer ou non sur le second angle.
Deux angles sont égaux s’ils ont le même écartement, s’ils se superposent parfaitement. Dans ce cas, les deux angles ont même mesure.
Somme de deux angles
Avec la souris, clique sur le curseur t et tire le vers la droite. L’angle de gauche se rapproche de l’angle droite.
Pour additionner géométriquement deux angles, il faut les rapprocher de telle façon que leurs deux sommets soient confondus et qu’un de leur côté soient aussi confondus. On obtient ainsi un nouvel angle qui est la somme des deux premiers.
Pour connaître la mesure du nouvel angle, on additionne les mesures des deux premiers.
Bissectrice d'un angle
En cliquant sur le bouton “Initialise”, on voit un angle en rose.
En cliquant sur le bouton “Construction de la bissectrice”, on voit apparaitre une demi droite partant du sommet A de l’angle . Cette demi-droite est la bissectrice de l’angle.
En cliquant sur le bouton “Angles égaux”, on voit que la bissectrice de l’angle le partage en deux angles égaux.
Propriété de la bissectrice d'un angle
Tu peux faire glisser le point M sur la bissectrice avec la souris. (Clique gauche sur le point M en déplaçant la souris).
Distance d’un point à une droite : c’est le plus court chemin entre le point et la droite. Ce plus court chemin est la longueur du segment perpendiculaire à la droite à partir du point.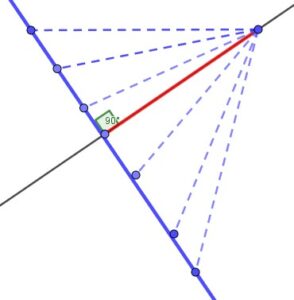
Lorsque le point M glisse sur la bissectrice les distances MB et MC sont toujours égales entre elles.
Constructions avec règle et compas.
Construire un angle égal à un angle donné.
Cliquer sur le bouton “initialiser/Démarrer” pour ramener le curseur t à zéro.
Cliquer à nouveau sur ce bouton pour démarrer l’animation.
Pour suspendre l’animation cliquer sur le petit triangle à côté de pause.
On peut aussi faire glisser le curseur avec la souris.
Construire un angle de 90°
Construire un angle de 60°
Angles opposés par leur sommet
Mettre le curseur sur 0 puis sur 1, puis sur 2.
Deux angles opposés par leur sommet sont deux angles qui ont même sommet et dont les côtés de l’un sont dans le prolongement des côtés de l’autre.
Ils sont engendrés par deux droites concourantes et dont le point de concoure est le sommet commun aux deux angles.
et 
sont deux angles opposés par leur sommet.
O est leur sommet commun. OD et OA sont dans le prolongement l’un de l’autre. Ainsi que OC et OB.
et 
sont aussi deux angles opposés par leur sommet pour des raisons semblables.
Angles complémentaires, supplémentaires
Angles complémentaires Faire glisser le curseur t vers la droite
Deux angles sont complémentaires si leur somme est égale à 90 degrés.
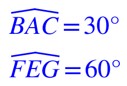
La somme de ces deux angles est égale à 90°
Les deux angles sont complémentaires.
Angles supplémentairesFaire glisser le curseur t vers la droite
Deux angles sont supplémentaires si leur somme est égale à 180 degrés.
La somme de ces deux angles est égale à 180°
Les deux angles sont supplémentaires.
Angles et droites
Faire glisser le curseur t vers la droite en s’arrêtant à chaque étape.
Soit deux droites parallèles d et d’.
Elles sont coupées par une autre droite Δ appelée sécante (sécant voulant dire couper : sécateur).
Ces trois droites forment à leur intersection 8 angles qu’il s’agit de déterminer. Pour cela on considère la position de ces angles par rapport aux deux parallèles et à la sécante.
Dans l’animation ci contre, plutôt que deux angles, on considère deux points et leur position par rapport à ces droites ( de t=-4 à t=0).
Ensuite on considère les angles et leurs propriétés (t=1 à t=12).