Taux de variation d’une fonction
- par gabriel
- dans Fonctions, Mathématiques
- sur 11 septembre 2022

Définition du taux de variation
Soit la fonction :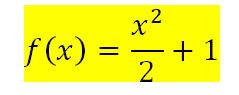
Dont la représentation graphique est la suivante :



Taux : c’est le rapport entre deux grandeurs
Rapport : c’est le quotient entre deux nombres.
Quotient : résultat de la division de deux nombres
Dans la fonction représentée ci-contre on a représenté les points A et B appartenant à la courbe de cette fonction.
A’ (x1)est l’abscisse du point A et A » (f(x1))sont ordonnée.
B’ (x2)est l’abscisse du point B et B »(f(x2)) son ordonnée.![]()
![]()
Le taux de variation peut se définir ainsi en français :
De combien varie la fonction f(x) pendant que x varie
Quel est la variation de la fonction f(x) par rapport à la variable x
Si on désigne par τ (lettre grecque tau) le taux de variation on peut écrire :
Variation signifie augmentation ou diminution ou encore mieux
accroissement ou décroissement (des verbes accroitre et décroitre).
Dans le cas particulier de la fonction ci contre, le taux de variation entre x1 et x2, entre A et B est :

Comme 3 est positif, c’est un accroissement.
Cela signifie que les f(x) ou les y s’accroissent 3 fois plus que les x.
Quand les x croissent de 1, les f(x) croissent de 3. Quand les x croissent de 2, les f(x) croissent de 6 etc.
Attention : Il faut bien conserver l’ordre des ordonnées et des abscisses. Si on commence par x1 au dénominateur, il faut commencer par f(x1) au numérateur.
Tangente


![]()
![]()
A et B appartiennent à la courbe. Les coordonnées de A et de B vérifient l’équation de la fonction.
Le taux de variation entre A et B est défini par :

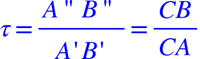
SI on considère le triangle rectangle en C, ABC,
CB est le côté opposé de l’angle α,
CA est le côté adjacent de l’angle α.
Or Dans un triangle rectangle, le côté opposé à un angle divisé par le côté adjacent de cet angle est égal à la tangente de l’angle. 
C’est aussi la pente ou coefficient directeur de la sécante AB.
Dans le cas représenté ci-contre :
Or ![]()
L’écart entre les deux valeurs provient du fait que la mesure de l’angle n’est pas une valeur exacte; cette valeur a été arrondie par le logiciel geogebra.
Taux de variation et sens de variation



Etudions le taux de variation entre les points a et O de la fonction ci-contre : ![]()
Ce taux de variation est négatif . Nous remarquons que entre A et O (sur l’intervalle [-30;0] la fonction est décroissante.
Etudions maintenant le taux de variation entre les points O et H:
Ce taux de variation est positif et nous remarquons que la fonction est croissante entre A et H (sur l’intervalle [0;30].
Démonstration :
Soit I in intervalle I=[x1;x2]. Sur cet intervalle, la fonction est monotone c’est-à-dire qu’elle n’est que croissante ou que décroissante ou que constante. 
La fonction est donc croissante.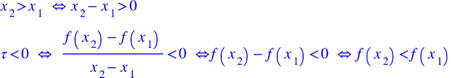
La fonction est donc décroissante.
La fonction est donc constante.
Taux de variation moyen


Le taux de variation d’une fonction représentée par une courbe est en fait un taux moyen.
Calculons par exemple pour la fonction ci-contre les taux de variation entre A et B , B et C, C et D, D et O, O et F ….![]()
![]()




En fait L’accroissement de la fonction (en rouge) entre A et B devrait être la longueur de l’arc AB (en rouge) et non pas en rapport avec la longueur de la corde AB (en bleu).
Or pour calculer la longueur d’un arc, nous avons besoin du centre et du rayon du cercle que nous ne connaissons pas.
de plus pour une fonction représentée par une courbe, le rayon appelé rayon de courbure change sans arrêt. Il est donc pratiquement impossible de calculer la longueur de l’arc AB.
Par contre si on diminue la longueur de AB, prenons AC on s’aperçoit que la longueur de l’arc AC s’approche de la longueur de la corde AC.
Et si on prend un point C de plus en plus près de A, l’arc AC va être pratiquement confondu avec la corde AC.
C’est ce que nous verrons dans le chapitre sur le nombre dérivé d’une fonction.