Point, droite, demi-droite, segment
Droites parallèles et perpendiculaires
Droites parallèles : définition
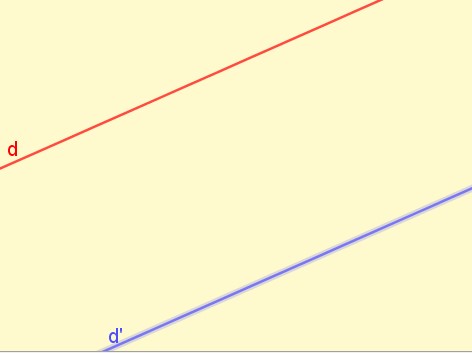
Deux droites sont parallèles si elles n’ont aucun point commun.
Deux droites parallèles ne se coupent pas.
On dit aussi qu’elles se coupent à l’infini.
(d) et (d’) sont parallèles.
Dans une portion de trajet rectiligne (en ligne droite), les rails d’un train sont parallèles.
Etymologie:
Du latin et du grec Para = à côté et allelon = l’un et l’autre.
Droites sécantes
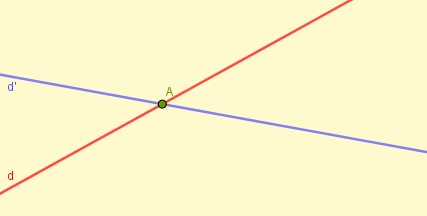
Deux droites qui ne sont pas parallèles se coupent en un point.
On dit qu’elles sont sécantes.
On dit aussi qu’elles sont concourantes.
A est leur point de concoure ou point d’intersection.
Etymologie:
sécant vient du latin secans signifiant coupant.
Sécante, intersection, sécateur….
Droites perpendiculaires
CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=189091
GPL, https://commons.wikimedia.org/w/index.php?curid=379414
Par aTarom — Travail personnelCámara: DiMAGE 7HiISO: 100Tv: 1/2Av: 9.5, Domaine public, https://commons.wikimedia.org/w/index.php?curid=963213
Deux droites perpendiculaires sont deux droites qui se coupent en formant un angle droit.
L’angle formé par les droites (d) et (d’) est égal à 90°.
Le point A est le pied de la perpendiculaire.
Etymologie
Perpendiculaire :
du latin perpendicularis, perpendiculum =fil à plomb, niveau.
Le fil à plomb est une ficelle au bout duquel est attaché une masse en plomb qui permet au maçon de construire un mur perpendiculairement au sol.
Le niveau à bulle est un instrument dans lequel est inséré une ampoule partiellement remplie d’eau et laissant apparaître une bulle d’air. Cela permet de construire des murs horizontaux ou verticaux.
Propriété 1
Si deux droites sont parallèles, toute perpendiculaire à l’une est perpendiculaire à l’autre.
Les droites (d1) et (d2) sont parallèles.
La droite (d) est perpendiculaire à la droite (d1).
Alors la droite (d) est perpendiculaire à la droite (d2).
Propriété 2
Si deux droites sont perpendiculaires à une même droite, elles sont parallèles.
La droite (d1) est perpendiculaire à la droite (d).
La droite (d2) est perpendiculaire à la droite (d).
Alors les droites (d1) et (d2) sont parallèles.
Propriété 3
Si deux droites sont parallèles, toute parallèle à l’une est parallèle à l’autre.
d1 est parallèle à d2.
d est parallèle à d1.
Alors, d est parallèle à d2.
Médiatrice d'un segment
Définition
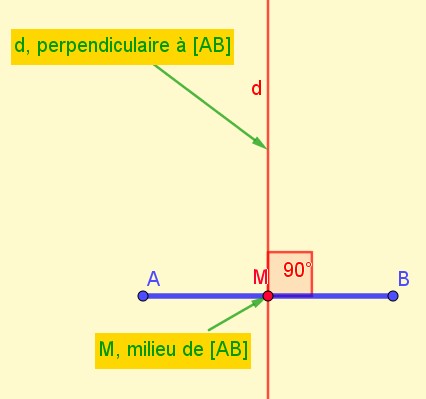
Soit le segment [AB], M est le milieu de ce segment.
La droite (d) est perpendiculaire au segment.
La droite (d) est la médiatrice du segment [AB].
Construction
Théorème et réciproque
Théorème
Réciproque
Tout point M de la médiatrice d’un segment [AB] est équidistant (à la même distance) des extrémités de ce segment.
Le point C est sur la médiatrice de [AB], il est le milieu de [AB] Donc CA=CB. Le segment [CM] est commun aux triangles ACM et BCM.
MC est la médiatrice de [AB], donc MC est perpendiculaire à [AB].
Les triangles ACM et MCM sont égaux (Un angle égal compris entre deux angles égaux). Ils sont parfaitement superposables. Ils sont symétriques par rapport à la médiatrice.
Tous leurs éléments homologues sont égaux et en particulier
MA=MB
Tout point M équidistant ( à la même distance) des extrémités d’un segment [AB] est situé sur la médiatrice de ce segment.
MA=MB.
Le triangle MAB est isocèle. 
C est le milieu de AB. CA=CB
Les triangles CMA et CMB sont superposables. Ils sont égaux (angle égal compris entre deux côté égaux).
Tous leurs éléments homologues sont égaux en particulier :
C est sur [AB].
donc 
C milieu de [AB] et MC perpendiculaire à [AB]
M est sur la médiatrice de [AB]
Ces deux théorème, le théorème direct et sa réciproque se résument dans la formule ci-dessous qu’on peut lire dans les deux sens :