Fonction logarithme népérien
- par gabriel
- dans Fonctions, Mathématiques
- sur 5 février 2021

Définition 1
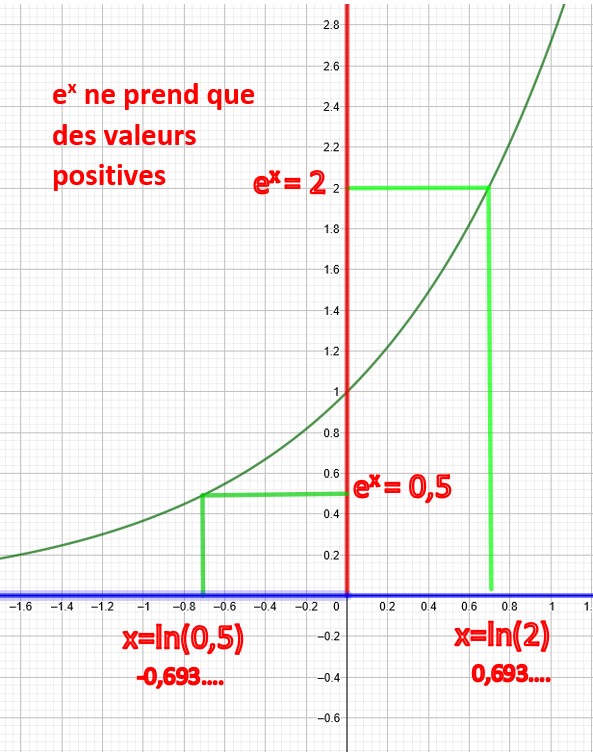

Solution de l’équation ex=k
Entre 0 et +∞ la fonction ex est continue et monotone.
Pour tout x∈]-∞;+∞[ les valeurs de ex∈ ]0;+∞[.
D’après le théorème des valeurs intermédiaires, il existe donc une solution et une seule telle que ex= k.
Il est difficile de trouver la solution de cette équation autrement que par le graphique, par le calcul. Aussi est-on obligé d’inventer de nouveaux nombres comme on l’a fait pour résoudre une équation du second degré. Ces nouveaux nombres, on les appelle logarithmes népériens de k. On note ln(k) et on prononce élène de k.
Ainsi la solution de l’équation ex=k est elle x=ln(k)
On verra par la suite que ces nouveaux nombres sont très pratiques pour les calculs. En effet avec des règles simples, il sera plus facile de manier ln(2) plutôt que 0,693 147 180 559 9 qui est en plus une valeur approchée de la solution de notre équation.
Pour tout x appartenant à l’intervalle ]0;+∞[, il existe une seule solution dans l’ensemble des réels de l’équation ex=k, cette solution est notée ln(k).
Ainsi l’ensemble des nombre x appartenant aux réels strictement positifs a pour image l’ensemble des nombres ln(k) appartenant à l’ensemble des réels.
x appartenant à l’ensemble ]0;+∞[ a une seule image ln(k) par la fonction ln appartenant à l’ensemble des nombres réels ]-∞;+∞[.
Et ln(k) appartenant à l’ensemble des nombres réels possède un seul antécédant x appartenant à l’ensemble des réels positifs.
La fonction ln est donc une bijection de ]0,+∞[ sur ]-∞;+∞[.
C’est la bijection réciproque de la bijection ex.
Définition 2


Fonction réciproque de la fonction
ex.
soit x un nombre appartenant à ]-∞;+∞[.
par la fonction exponentielle népérien x a pour image ex.
ex appartient à ]0;+∞[.
Par la fonction logarithme népérien ex qui appartient à ]0;+∞[ a pour image x .
Le logarithme de l’exponentielle d’un nombre x est égal à x.
L’exponentielle du logarithme d’un nombre x est égal à x.
Les deux fonctions sont réciproques.
La fonction logarithme népérien est la réciproque de la fonction exponentielle .
Or Deux fonctions réciproques ont une représentation graphique symétriques par rapport à la première bissectrice du graphe d’équation y=x.
f(x)=ex est représentée par la courbe verte. On remarque les valeurs particulières pour x=0 et x=1. f(x) est définie sur ]-∞;+∞[. Comme cette fonction ne s’annule pas et est toujours positive, les images de x appartiennent à l’intervalle ]0;+∞[.
ln(x) est représentée par la courbe rouge. On remarque les valeurs particulières pour x=1 et x=e. Cette fonction est définie sur ]0;+∞[ et prend ses valeurs sur ]-∞;+∞[.
Si x >1 ln(x)>0
Si x<1 ln(x)<0
Définition 3








Primitive de la fonction inverse s’annulant pour x=1
Calcul de la primitive de la fonction inverse :
f(x)=1/x peut s’écrire f(x)=x-1.
A partir de là on ne peut pas calculer la primitive avec les formules classiques. En effet F(x)=x-1+1/-1+1+cte=x0/0+cte, le résultat n’a aucun sens compte tenu de la division par 0.
Aussi est-on dans l’obligation de construire une nouvelle fonction numérique nommée logarithme népérien, notée ln ou parfois Ln (Autrefois Log avec L majuscule). Cette fonction est définie ainsi :
Le logarithme népérien est l’unique primitive de la fonction x-1 s’annulant pour x=1.
On peut écrire aussi que le logarithme népérien de a est égal à la somme des rectangle de fargeur dx et de fongueur x-1.
Ainsi tout nombre a appartenant à l’intervalle ]0;+∞[ possède-t-il une image et une seule dans l’ensemble des nombres réels; Cette image est appelée ln(a).
De ce fait, on a défini une nouvelle fonction ln(x) qui a tout x non nul et positif associe une image ln(x) dans l’ensemble des réels.
Dans un premier temps ln(x) n’est définie que pour x positif.
Pour les x négatifs, nous définissons la fonction logarithme de la valeur absolue de x : lnΙxΙ.
la dérivée de cette fonction est bien x-1 soit 1 sur x.
En effet lnΙxΙ lorsque x<0 est une fonction composée (ΙxΙ=-x). Donc ln(-x). calculons la dérivée de cette fonction :
x→-x→ln(-x) ;
La dérivée de ln(-x) est égale au produit de la dérivée de -x soit -1 par la dérivée ln(-x)=-x-1. Soit -(-x-1)= x-1.
Ainsi lnΙxΙ est une primitive de f(x)=x-1 sur ]-∞;+∞[.


Dans un premier temps ln(x) n’est définie que pour x positif non nul.
Voyons s’il est possible de définir une fonction semblable pour tout x réel.
Soit la fonction f(x)= lnΙxΙ. C’est à dire la fonction logarithme de la valeur absolue de x.Pour les x négatifs, nous définissons la fonction llnΙxΙ, lorsque x<0, est une fonction composée (ΙxΙ=-x). Donc ln(-x). calculons la dérivée de cette fonction :
x→-x→ln(-x) ;
La dérivée de ln(-x) est égale au produit de la dérivée de -x soit -1 par la dérivée ln(-x)=-x-1. Soit -(-x-1)= x-1.
Ainsi lnΙxΙ est une primitive de f(x)=x-1 sur ]-∞;+∞[.
Si x <0 la fonction lnΙxΙ (ln de la valeur absolue de x) est définie et prend ses valeurs sur l’ensmble des réels.
Propriétés algébriques
![]()
Cette propriété découle de la définition. il n’y a donc pa s lieu de la démontrer.
![]()

∞
Soit a un nombre réel strictement positif : a>0.
soit la fonction définie sur l’ensemble des réels strictement positifs :
f(x)= ln(ax)-ln(x).
Elle est continue et dérivable sur l’ensemble considéré :]0;+∞[.
Sa dérivée est ![]() .
.
Puisque la dérivée de la fonction est nulle, cela signifie que la fonction est une fonction constante. f(x)=C.
Pour calculer cette constante, il suffit de prendre une valeur de x quelconque. On va prendre x=1 pour que les calculs soient simples.
Pour x=1 : f(1)=a-ln1=C. Donc C=ln(a)
f(x)=C donc ln(ax)-ln(x)=C soit ln(ax)-ln(x)=ln(a)
Et ainsi ln(ax)=ln(a)+ln(x).


Si a est différent de 0, on peut écrire :
Appliquons la propriété précédente :
donc:

Donc :


En utilisant la propriété précédente :
![]()
![]()
Toujours, en utilisant l’une des propriétés précédentes :


Pour![]()
En prenant le problème à l’envers, on peut écrire : ![]()
Donc en lisant à l’envers nous avons :![]()
d’où :![]()
Dérivée



Première démonstration :
On admet que ln(x) est dérivable sur ]0;+∞[.
ln(x) et ex sont deux fonctions réciproques. on peut donc écrire eln(x)=ln(ex)=x.
Puisque ![]() , dérivons les deux membres de cet équation :
, dérivons les deux membres de cet équation :![]()
Appliquons dans le premier membre le théorème des fonctions composées pour calculer sa dérivée. ![]()
Nous en déduisons :![]()
![]()
![]()
Seconde démonstration :
On suppose que la fonction ln est continue sur ]0;+∞[. Ainsi on peut utiliser la définition de la dérivée. Attention, il faut s’accrocher !
La dérivée en un point d’abscisse x0 de la courbe est égale à la limite lorsque x tend vers x0 de l’accroissement des f(x) divisé par l’accroissement des x .![]()
Pour faciliter les calculs, nous allons procéder à un changement de variable :![]()
La nouvelle écriture donne :![]()
si on prend l’inverse de l’inverse de l’expression entre crochets, on garde la même valeur. Ca sert à rien mais cela permet de mettre en évidence la dérivée de la fonction exponentielle.
En effet le dénominateur correspond à la définition de la dérivée de la fonction exponentielle.
Comme la dérivée de la fonction exponentielle est la fonction exponentielle elle-même :![]()
Ainsi pour tout x0 appartenant à l’intervalle ]0;+∞[, il existe un nombre dérivé et donc sur cet intervalle il existe une fonction dérivée![]()
Limites
On prend les limites aux bornes du domaine de définition ]0;+∞[.
1) limites de ln(x) quand x tend vars +∞:
Soit A un nombre réel.
Si on choisit x> eA, alors ln(x)>ln(eA) donc ln(x)>A.
Ainsi ln(x) ∈]A;+∞[.
On peut prendre un nombre A très grand, lnx appartiendra toujours à cet intervalle ]A;+∞[, intervalle qui se rapproche toujours de +∞.
Donc quand x tend vers +∞, ln(x) tend vers +∞.
Voir les définitions des limites.
2) limite de ln(x) quand x tend vers 0 par valeurs positives, (à droite de 0, tend vers 0+).
Soit ![]() ⇒
⇒ ![]()
Faire tendre x vers 0+ revient à faire tendre son inverse X vers +∞.
Ainsi :![]()