Généralités sur les fonctions
Approche intuitive
Une fonction est une machine à transformer un nombre en un autre nombre.
J’introduis dans la machine un nombre particulier, 5.
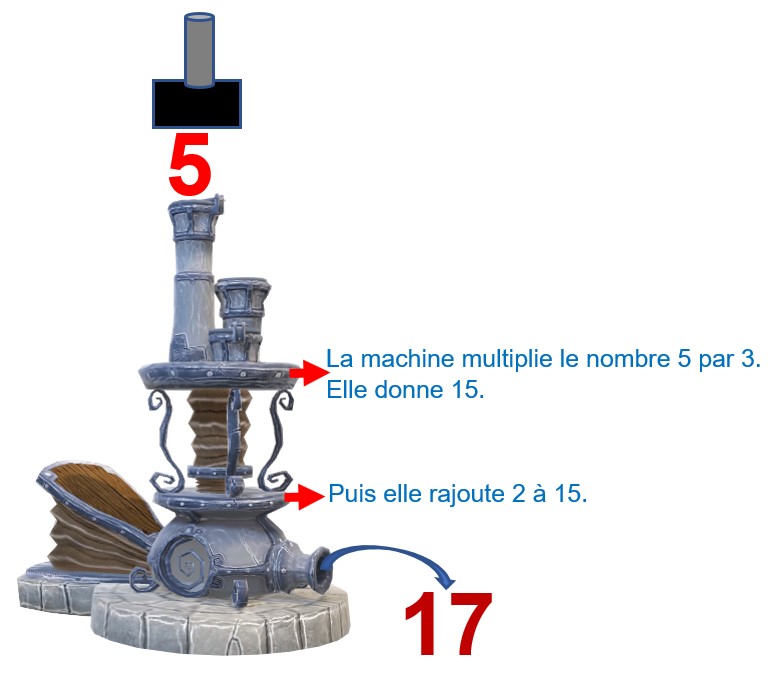
je peux écrire que 17 est égale à 3 multiplié par 5 plus 2.
J’ai introduis 5 et il ressort 17.
La fonction f de ma machine consiste à transformer 5 en 5×3+2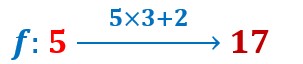
J’introduis dans la machine un nombre quelconque représenté par x .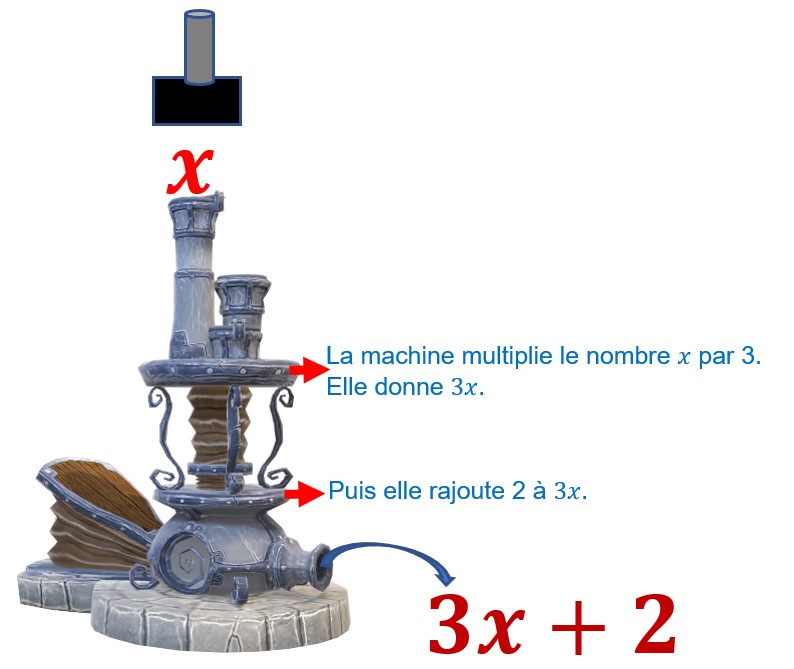
Je peus écrire que 3x+2 est égal à 3 multiplié par x plus 2.
J’ai introduis x, il ressort 3x+2.
La fonction f de ma machine consiste à transformer n’importe quel nombre x en un nombre 3x+2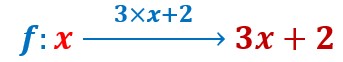
J’ai réglé ma machine autrement.
Je lui introduis un nombre particulier 7.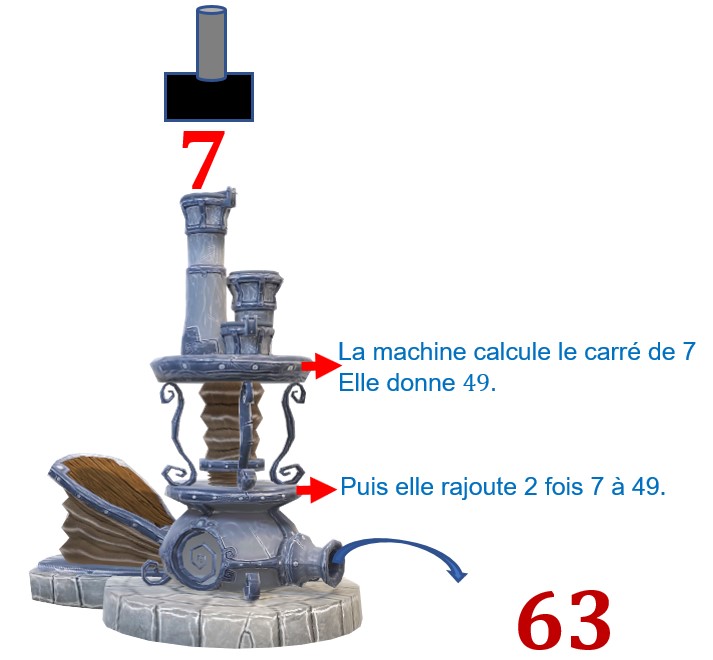
Je peux écrire que 63 est égal à 7 au carré plus deux fois 7. 
J’ai introduis 7 et il ressort 63.
La nouvelle fonction g de ma machine consiste à transformer
7 en 7²+2×7.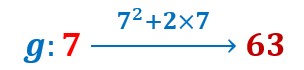
J’introduis dans la machine un nombre quelconque représenté par x.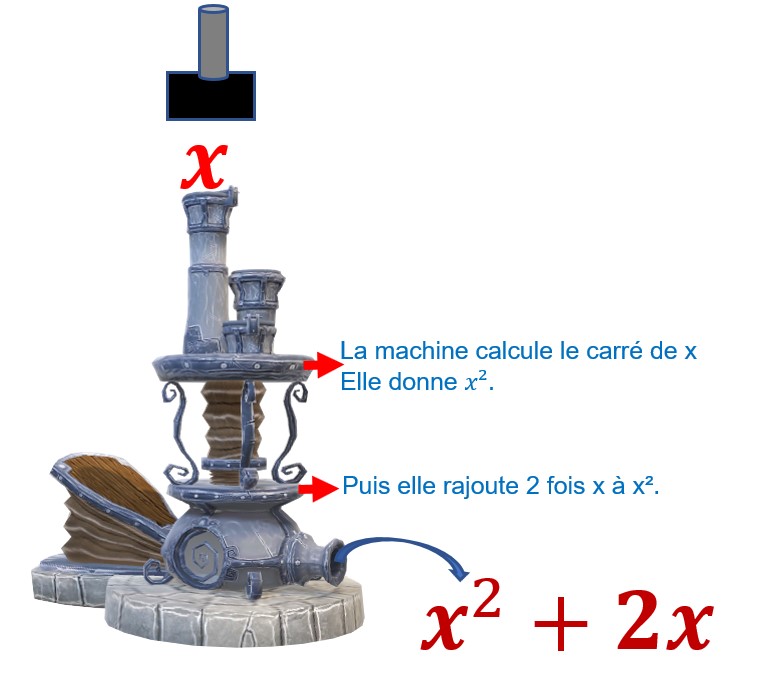
Je peux écrire que x²+2x est égal au carré de x plus le double de x.
J’ai introduis x et il ressort x²+2x.
La nouvelle fonction g de ma machine consiste à transformer un nombre quelconque x en x²+2x.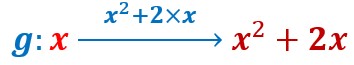
Définitions
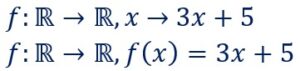
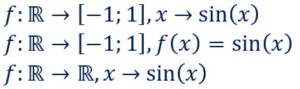
Remarques :
Chaque nombre x ne peut avoir qu’une seule image f(x).
Mais chaque image peut avoir un ou plus antécédent.
L’ensemble de départ est souvent appelé aussi ensemble de définition. C’est l’ensemble qui pour chacun de ses éléments aura une image. On peut ne pas toujours trouver une image de x suivant les fonctions.
Dans les fonctions ci-contre, on peut toujours trouver une image de chaque élément de l’ensemble de départ x.
Graphe
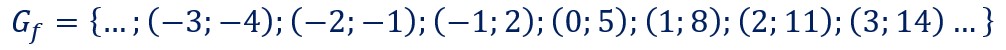
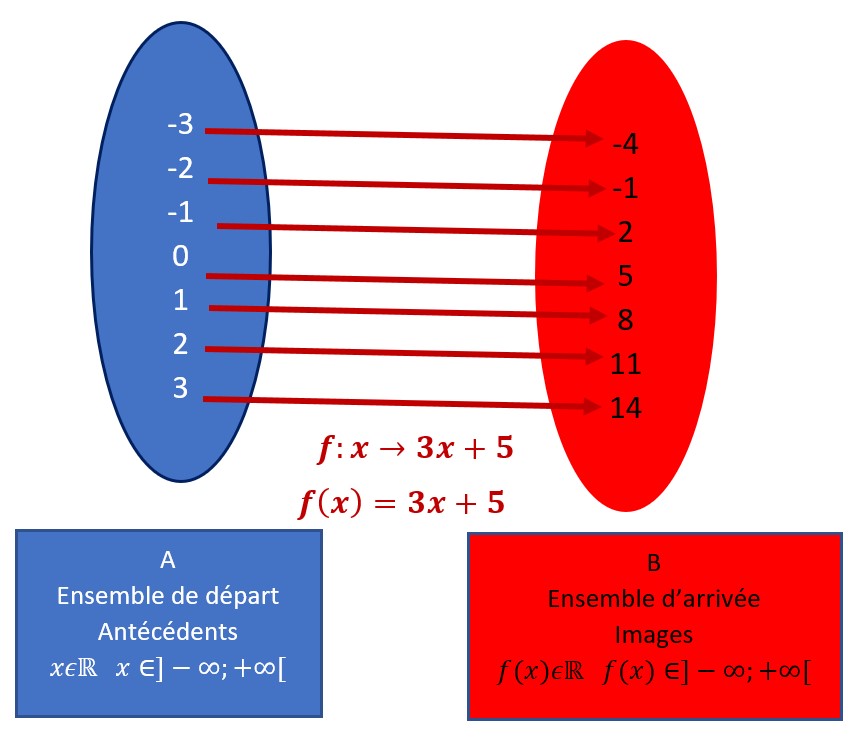
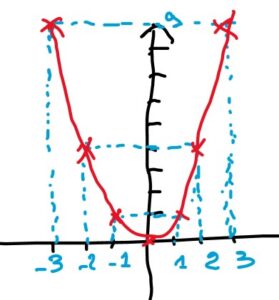
Ci-contre est représenté l’ensemble de départ en bleu dans lequel nous avons noté une seule partie des nombres x possibles de -3 à 3.
Dans l’ensemble d’arrivée en rouge ne sont représentées que les images des nombres de l’ensemble de départ.
Ainsi nous obtenons une série de couples (antécédent; image) (x;f(x)) :
…(-3;-4) (-2;-1) (-1;2) (0;5) (1;8) (2;11) (3;14)…
Il existe une infinité de ces couples.
il est impossible de tous les représenter.
On appelle graphe cet ensemble de couples propre à la fonction considérée. On le note Gf.
Ne pas confondre graphe qui est un ensemble de couples avec la représentation graphique de la courbe qu’on va voir ci-dessous.
Pourtant, souvent, abusivement on désigne par graphe, la représentation graphique. Parfois l’usage manque de précision.
Tableau de valeurs
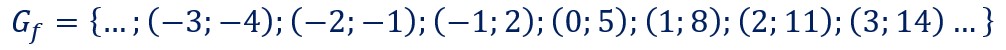
Plutôt que d’établir un graphe comme ci-contre , on dresse un tableau de quelques valeurs de la fonction. Ce qui permettra de construire la représentation graphique de la fonction.
Représentation graphique
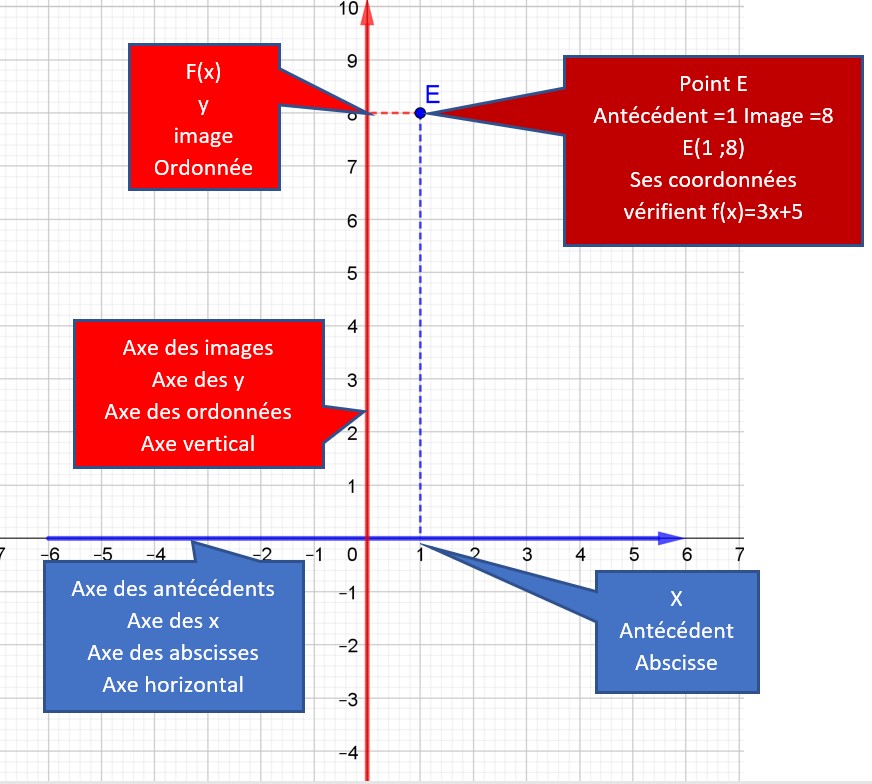
Soit un axe gradué horizontal, en bleu. C’est l’axe des abscisses.
Soit un axe gradué vertical, en rouge. C’est l’axe des ordonnées.
Les deux axes forment un repère, grâce à qui on pourra repérer des points.
Les deux axes sont ici perpendiculaires, orthogonaux. Ils constituent un repère orthogonal.
les deux axes ont des unités égales. Le repère orthogonal est ainsi normé (aux mêmes normes sur les deux axes.
C’est un repère orthonormé.
Le point E a pour abscisse 1 et pour ordonnée 8.
On a obtenu 8 grâce à la fonction f(x)=3x+5 : f(1)=3.1+5=8
1 est l’antécédent, celui à partir duquel on calcule.
8 est l’mage de 1 par la fonction f(x)=3x+5
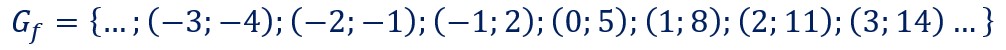
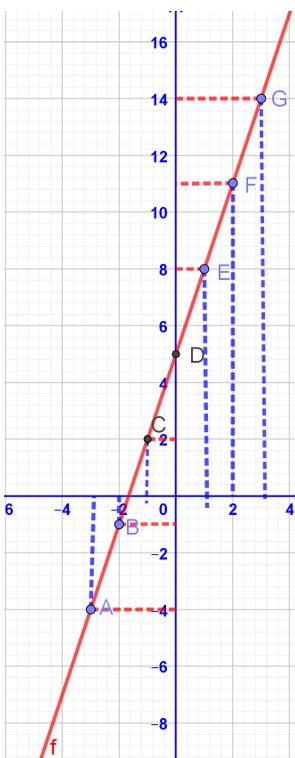
A partir du graphe ci-dessus ou à partir du tableau de valeurs, on positionne chaque point A,B,C,D,E,F,G selon son abscisse et son ordonnée.
En joignant les points, on obtient une droite.
Cette droit est la représentation graphique de la fonction f(x) = 3x+5
Chaque point de la droite vérifie l’équation f(x) = 3x+5.
Si on prend un point quelconque de cette droite, son ordonnée sera égale à 3 fois sont abscisse plus 5.
En d’autres termes, l’image d’un nombre x appelé antécédent est égale à 3 fois ce nombre +5.
En règle général, pour construire la courbe représentative d’une fonction :
Par exemple 
je calcule les coordonnées de plusieurs points en utilisant la formule donnée,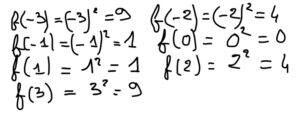 
je les dresse dans un tableau,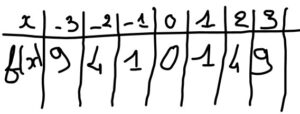
je positionne les points dans un graphique, je joins les points.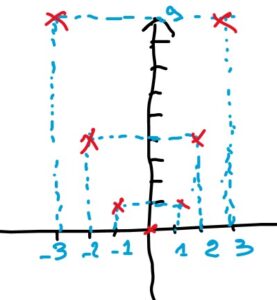
Images et antécédents d'une fonction.
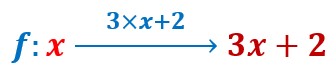
Ci-contre, la première manière d’écrire une fonction.
On désigne cette fonction par une lettre quelconque, f par exemple.
Un nombre x est choisi. On calcule son image grâce à la formule donnée.
Seconde manière d’écrire une fonction, la plus pratique.
L’image f(x) de x par la fonction f est donnée par la formule du deuxième membre 3x+2.
On lit : f de x = 3x+2. Ce qui signifie : l’mage f(x) de x par la fonction f est égale à 3 fois x +2.
L’image f(2) de 2 par la fonction f est égale à 3 fois 2 plus 2 soit 8
f(2)=8.
On appelle 2 antécédent.
On appelle f(2) image.
Elle est déterminée par l’une des deux formules ci-dessus.
On peut envisager une autre fonction g qui sera différente.
C’est le nombre dont on va calculer l’mage.
Ce le nombre qu’on introduit dans la machine.
Il est indiqué en rouge dans cette page.
Il est situé sur l’axe des abscisses.
C’est le résultat lorsqu’on a traité l’antécédent par la fonction.
Elle est indiquée en marron dans cette page.
Elle est située sur l’axe des ordonnées.
Calculer l’image.
Soit la fonction :
Calculons l’image de 2.
Cela signifie que 2 est l’antécédent.
Notons en rouge l’antécédent dans cette fonction. 
Remplaçons x par 2 :
L’image de 2 par la fonction f est 6.
Calculer l’antécédent .
Soit la même fonction,
Calculons l’antécédent de 7
Cela signifie que 7 est l’image.
Donc on peut écrire :
Mais on sait aussi que :
f(x) est égal, à la fois à 7 et à 4x-2. Ou mieux 7 est égal à F(x) et 4x-2 est aussi égal à f(x) donc 7 est égal à 4x-2, ou 4x-2 est égal à 7.
Il reste à résoudre cette équation. 
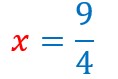
L’antécédent de 7 est 9/4.
Calculer l’image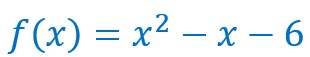 
Calculer l’image de 5 par la fonction f ci-dessus.
Il suffit de remplacer x par 5 et de continuer les calculs.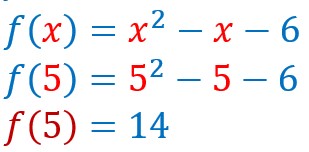 
L’image de 5 par la fonction f est 14.
Calculer l’antécédent.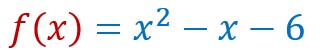
Calculer l’antécédent de 24 dans la fonction f ci-dessus. Si on demande l’antécédent de 24, cela signifie que 24 est l’image.
Il suffit donc d’égaliser les deux valeurs de f(x), de continuer les calculs pour obtenir une équation du second degré.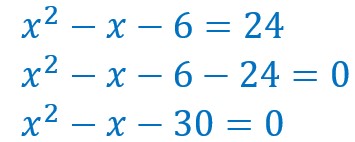
Il suffit de résoudre cette équation pour trouver x.
Calcul de delta: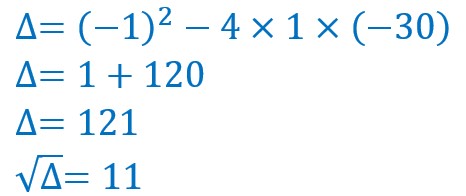
Δ étant positif nous aurons deux racines, donc deux solutions pour x :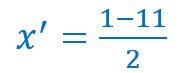
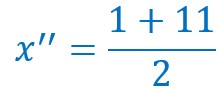
24 a donc deux antécédents.
Domaine ou ensemble de définition
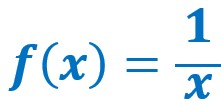
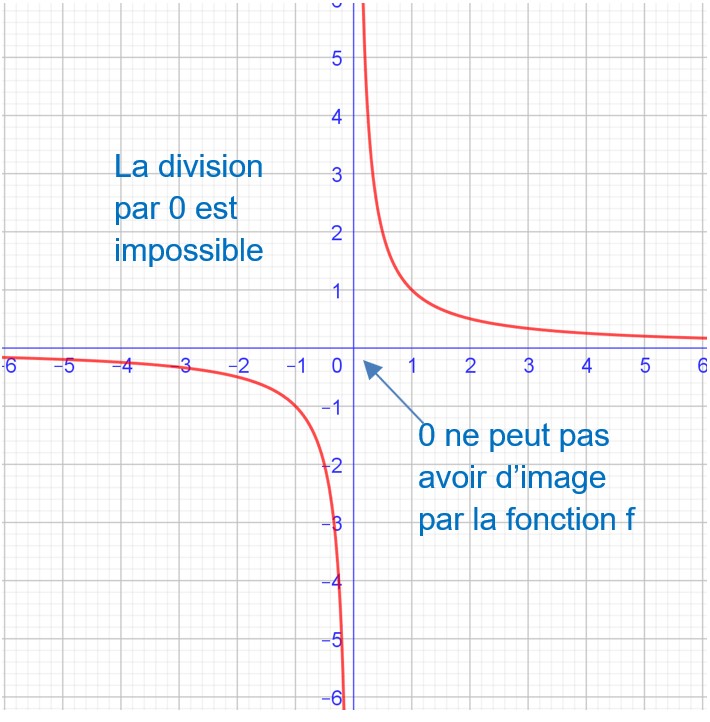
Pour certaines fonctions, il n’est pas toujours possible de calculer l’image de quelques nombres x.
Par exemple, pour la fonction inverse
on ne peut pas trouver d’image à x=0 puisque la division par 0 n’a pas de sens .
On peut trouver les images pour tous les x appartenant aux nombres réels sauf 0.
Le domaine de définition de la fonction f va de -∞ jusqu’à s’approcher de 0 le plus possible( indéfiniment) mais sans jamais être égal à 0; puis des nombres positifs très proches de 0 jusqu’à +∞.
L’ensemble de définition est noté, ici, en extension.
On voit très bien ainsi sur quel domaine est étudié la fonction f.
Autre manière de dire la même chose : x appartient à l’ensemble moins l’infini, zéro union zéro ,plus l’infini.
Ici encore le domaine de définition est noté en extension. 
encore une autre manière : l’ensemble de définition de la fonction f est l’ensemble ℜ étoile c’est à dire l’ensemble ℜ en entier sauf zéro (ce qu’indique l’étoile).
Là l’ensemble de définition est noté en compréhension. Cela ne permet pas de voir facilement cet ensemble.
Pour la suite, il est important de noter l’ensemble de définition en extension :
cela permettra de calculer les limites aux bornes de cet ensemble, c’est-à-dire en -∞, en 0 à gauche, en 0 à droite, en +∞.
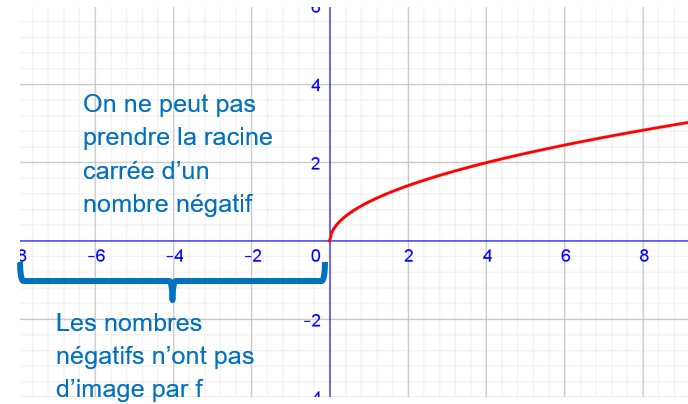
Autre impossibilité :
On ne peux prendre la racine carré que d’un nombre positif ou nul. Pour la fonction
x possède une image si et seulement si 
.
On peut prendre x compris entre 0 compris et + l’infini.
x peut-être pris dans l’ensemble des réels positifs, y compris 0 (il n’y a pas d’étoile).
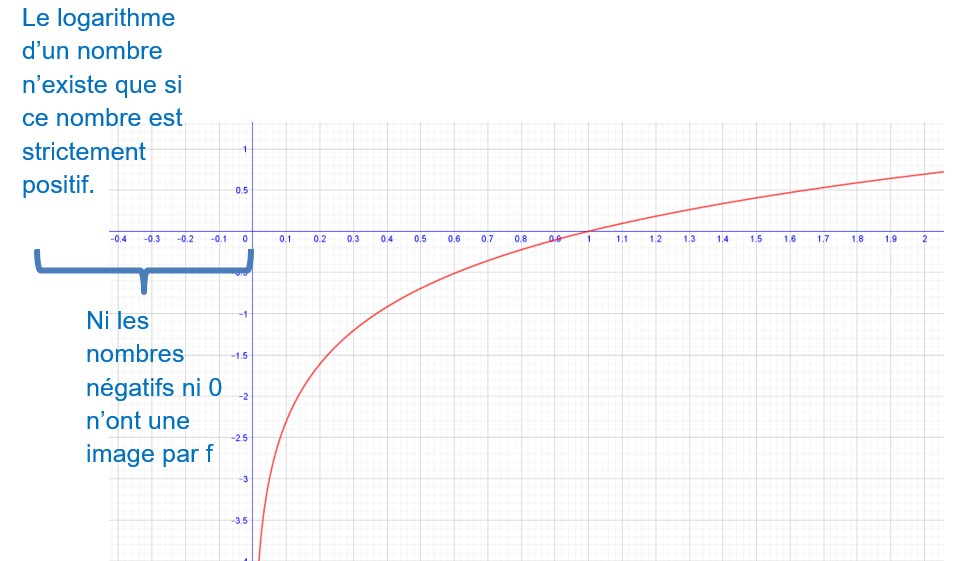
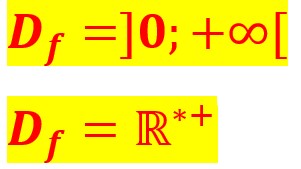
Une autre impossibilité :
le nombre dont on prend le logarithme népérien doit être à la fois positif et différent de 0. Il doit être strictement positif.
On peut prendre x le plus près possible de 0 : 0,1 0,01 0,001 0,0001 0,000000000000001, mais on ne peut pas prendre x égal exactement à 0. 0 est exclu du domaine de définition.
Le domaine de définition est l’ensemble des nombres réels allant de 0, non compris, jusqu’à plus l’infini.
Le domaine de définition est l’ensemle des nombres réels positifs privé de 0
Comment trouver le domaine de définition de cette fonction.
Nous remarquons d’abord que cette fonction est une fraction et qu’elle possède des inconnues x au dénominateur.
Or le dénominateur d’une fraction ne doit pas être égal à 0; on écrit mathématiquement que ce dénominateur doit être différent de 0.
Il est évident que pour qu’un produit de facteurs soit différent de 0 il faut que ses deux facteurs soient différents de 0,
Donc :
Traçons la droite des nombres avec ces résultats :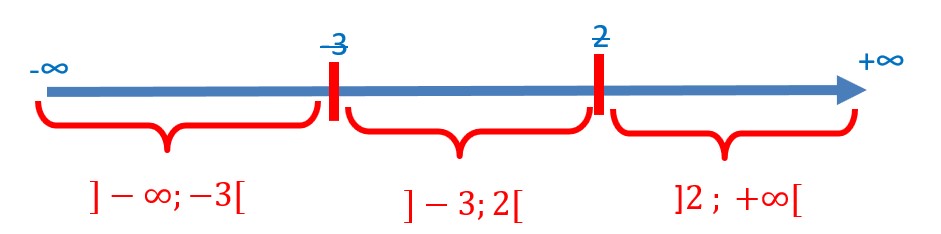
On peut écrire aussi que le domaine de définition est l’ensemble des réels privé des nombres -3 et 2 :
Trouver le domaine de définition de :
Puisqu’on ne peut prendre la racine carrée que d’un nombre positif ou nul, l’expression placée sous le radical ne peut-être que positive ou nulle.
Ecrivons le sous forme mathématique :
Il s’agit d’une inéquation avec un trinôme du second degré. Il nous faut calculer les racines de ce trinôme s’il y en a. 
Le discriminant est positif, il existe donc deux racines. 
Dans ce cas le trinôme est du signe du coefficiant de x² à l’extérieur des racine et du signe contraire de ce coefficiant entre les racines.
Or ce coefficiant a=1 dans ce cas est positif.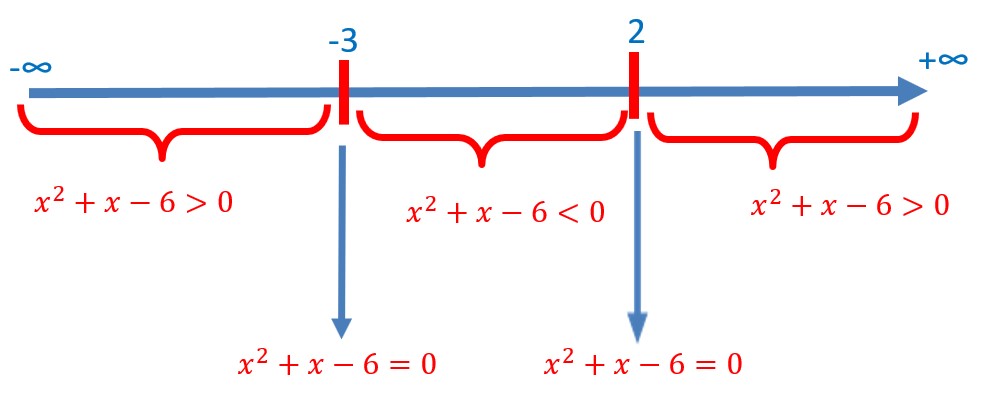 
Nous en déduisons le domaine de définition. 
Trouver le domaine de définition de :
A l’intérieur du crochet on remarque une identité remarquable sous forme développée. Factorisons la. 
On obtient ainsi un produit de trois facteurs.
Pour en connaître le signe, établissons un tableau.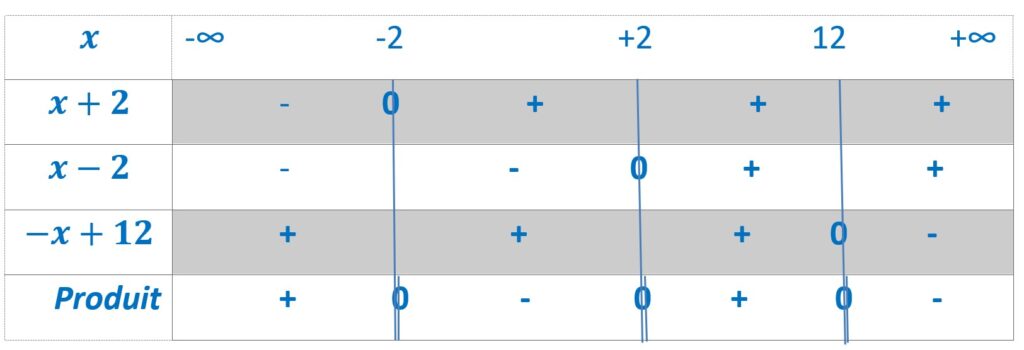
Nous savons qu’on ne peut prendre le logarithme népérien d’un nombre que si ce dernier est à la fois positif et différent de 0.
Nous en déduisons le domaine de définition de notre fonction. 
On aurait pu traiter x²-4 comme un trinôme du second degré, trouver son signe en fonction des valeurs de x, puis établir un tableau avec le facteur -x+12. Mais cela compliquait le problème.
Parité d'une fonction
Fonction paire :
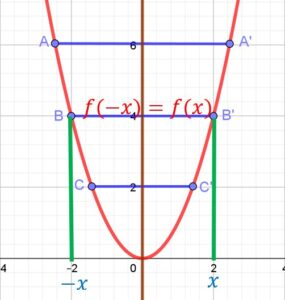
soit la fonction:
Calculons f(-x) en changeant x en -x :
Or (-x)²=x²
Mais :
Donc :
Le point A d’abscisse -2,44 est symétrique au point A’ d’abscisse 2,44,
ils ont tous deux 6 pour ordonnée
Le point B d’abscisse -2 est symétrique au point B’ d’abscisse 2.
Ils ont tous deux la même ordonnée 4.
Il en est de même des points C et C’.
Fonction impaire.
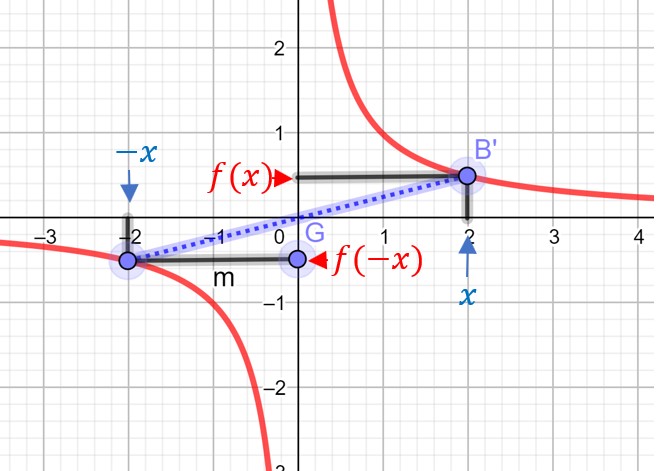
Soit la fonction 
calculons f(-x) en chabgeant x en -x
Soit, en enlevant la parenthèse 
Un nombre positif 1 divisé par un nombre négatif -x donne un résultat négatif. 
Or
c’est justement f(x). Donc 
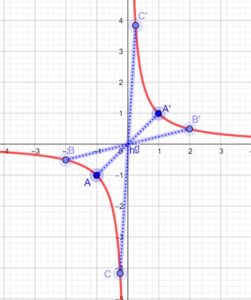
Sur le graphique ci contre on a f(2)=0,5 et f(-2)=-0,5
Les points A’,B’,C’ sont bien respectivement symétriques aux points A,B,C par rapport à O, l’origine du graphique.
Fonctions périodiques
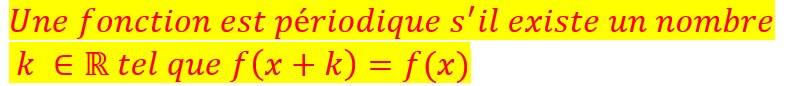
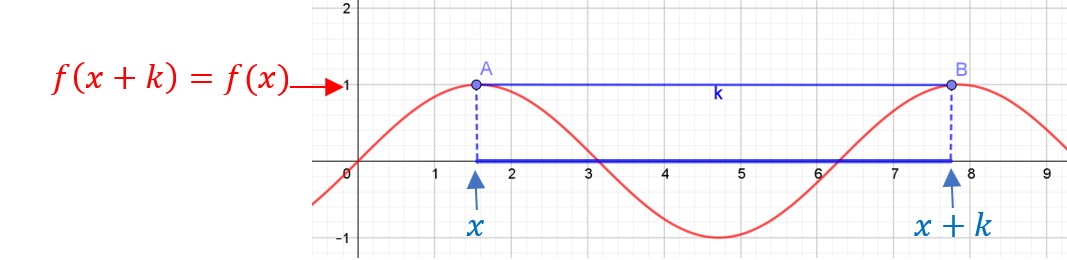
On voit bien sur la figure ci-contre que la fonction se reproduit à l’identique pour tout x et x+k.
C’est donc une fonction périodique.
Ici c’est la fonction sinus.
On sait que le sinus d’un angle varie entre -1 et 1.
On sait aussi que le sinus d’un angle x+2π soit x+6,28 est égal au sinus de l’angle x.
Dans ce cas la période k est égale à 2π doit à 6,28.
Composition de fonctions
Soient deux fonctions :
qui, à un élément x de l’ensemble A fait correspondre par f un élément f(x) de l’ensemble B .
qui, à un élément f(x) de l’ensemble B fait correspondre par g un élément g(x) de l’ensemble D.
Si 
c’est-à dire si tous les éléments de l’ensemble B appartiennent aussi à l’ensemble C (B est inclus dans C), alors il existe une fonction, appelée fonction composée de g et f .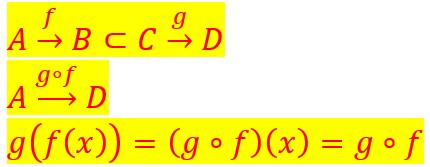
Cela peut paraître compliqué, mais les exemples ci contre devrait faciliter les choses.
Soient les deux fonctions :
Calculer la fonction la fonction composée de ces deux fonctions
On peut établir un diagramme: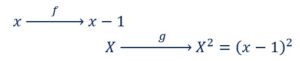
On cherche l’image de x par f , on appelle cette image X. Il faut trouver l’mage de X par g qui est X². Comme X est égal à (x-1), on le remplace par cette valeur.
On aurait pu écrire aussi :
Calculons maintenant 
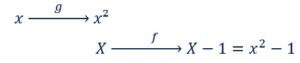
Donc :
La composition des fonctions n’est pas commutative.
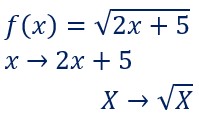
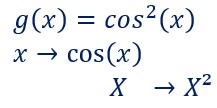
Il est parfois utile, notamment pour le calcul des dérivées, de reconnaître une fonction composée.
Dans la première f(x), on calcule l’image de x par 2x+5 puis on prend la racine carrée du résultat 2x+5
Dans la deuxième g(x) on cherche d’abord la valeur de cos(x) puis on prend la carré de cette valeur.