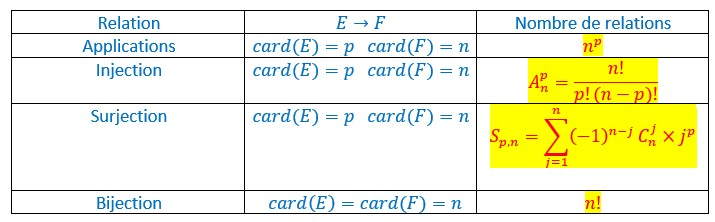
Dénombrements
Menu
Les ensembles
Représentation presque réelle d’un ensemble.
Représentation en extension :
Représentation en compréhension :
Autre exemple :
Un ensemble est une collection d’objets.
Ces objets sont les éléments de l’ensemble.
Un ensemble peut être fini ou infini.
On peut définir un ensemble de deux manières :
par extension, en notant dans une accolade tous les éléments de l’ensemble.
par compréhension en le nommant par une propriété caractéristique commune à tous ses éléments.
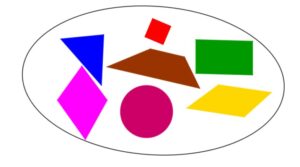
On a coutume de représenter un ensemble dans un cercle, appelé diagramme de Venn, ou plus communément patate.
Ci-contre, on a représenté les figures géométriques dans une patate. Chacun des éléments de cet ensemble sont nommés : triangle, parallélogramme, ….
Les éléments d’un ensemble sont séparés par des points virgules lorsque l’ensemble est exprimé en extension.
On note qu’un élément appartient à un ensemble par le signe ∈
On note qu’un élément n’appartient pas à une ensemble par le signe ∉
Intersection de deux ensembles
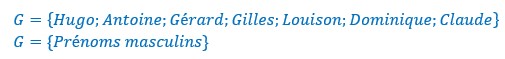
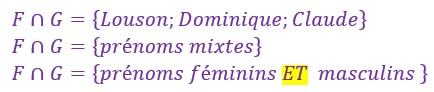
Soit un ensemble de prénoms féminins en rouge .
Soit un ensemble de prénoms masculins en bleu .
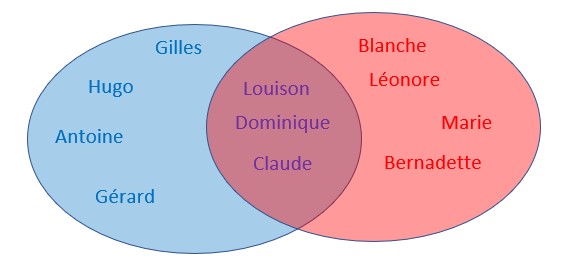
Ces deux ensembles possèdent 3 éléments en commun, des prénoms pouvant être porter soit par des filles soit par des garçons.
Ces trois éléments appartenant aux deux ensembles forment l’intersections de ces deux ensembles.
L’intersection de ces deux ensembles est constitué des prénoms qui sont à la fois féminins ET masculins.
Les deux ensembles et leur intersection, sont représentés par le diagramme de Venn ci-contre (Patates).
L’intersection est représentée par un U renversé : ∩ que l’on peut lire “intersection” ou “inter”.
Ainsi F inter G est un ensemble de 3 prénoms : Louison; Dominique et Claude.
Réunion de deux ensembles
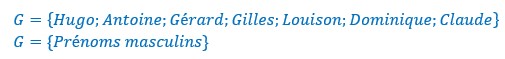
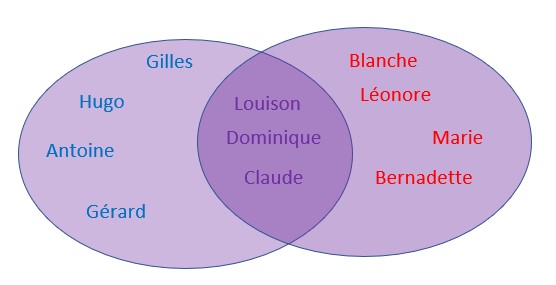
Nous reprenons les deux ensembles précédents.
Si on les réuni, on obtient un ensemble dont les éléments sont les prénoms féminins ou masculins.
La réunion de ces deux ensembles est constitué des prénoms soit féminins, soit masculins donc féminins OU masculins.
La réunion de deux ensembles est représentée par un U majuscule : ∪, que l’on peut lire union. Ainsi F union G est constitué de tous les éléments de F et de tous les éléments de G.
Mais on s’aperçoit que si on ajoute tous les éléments de G à tous les éléments de F dans la formule en extension, certains éléments, les prénoms mixtes sont répétés deux fois.
Or dans un ensemble, chacun des éléments est unique et ne peut donc être nommé qu’une seule fois.
Il nous faut donc enlever une fois ces éléments qui se répètent.
On enlève en fait l’intersection des deux ensembles.
Si les deux ensembles n’ont pas d’intersection, il est évident qu’on n’enlève rien.
Ensembles disjoints
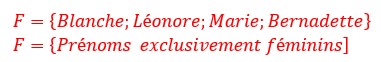
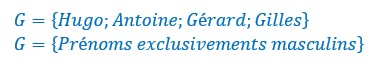
Des ensembles disjoints sont des ensembles qui n’ont pas d’intersection, qui n’ont aucun élément commun.
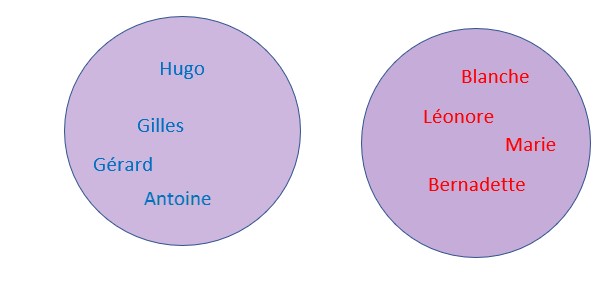
Soit les deux ensembles F et G de prénoms de garçons et de filles.
Ces deux ensembles n’ont pas d’éléments en commun, ils n’ont pas de prénom mixte. Ils sont disjoints.
Leur intersection est l’ensemble vide représenté par un zéro barré.
Sous ensembles
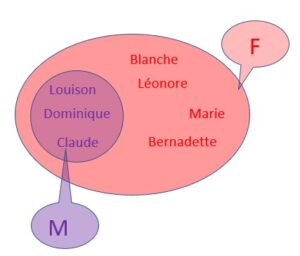
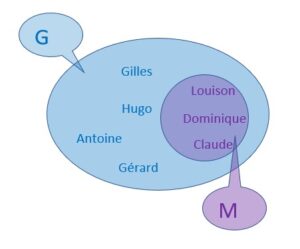
Dans l’ensemble des prénoms féminins F, on peut isoler certains éléments comme Louison, Dominique et Claude.
Ces éléments constituent un sous ensemble de F.
On peut appeler M ce sous ensemble, le sous ensemble des prénoms mixtes.
On peut noter que l’ensemble M est inclus dans l’ensemble F, on peut dire aussi que M est contenu dans F. On utilise le signe ⊂.
Si on isole le sous ensemble M dans F, il reste les éléments Blanche, Léonore, Marie, Bernadette. Ces éléments constituent le complémentaire de M dans F. On le note en écriture manuscrite par 
De même les éléments Blanche et Léonore constituent un sous ensemble de F…
On peut procéder de manière identique avec l’ensemble G
Propriétés
Union et intersection avec l’ensemble vide :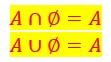
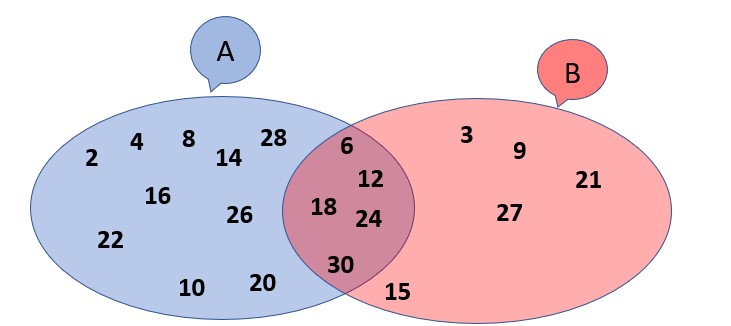
Union, intersection avec inclusion :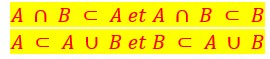
Autres relations : 
Il est évident que l’intersection ou la réunion d’un ensemble avec l’ensemble vide donne cet ensemble
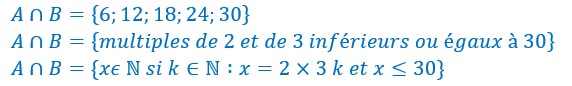
Les deux autres relations sont également évidentes.
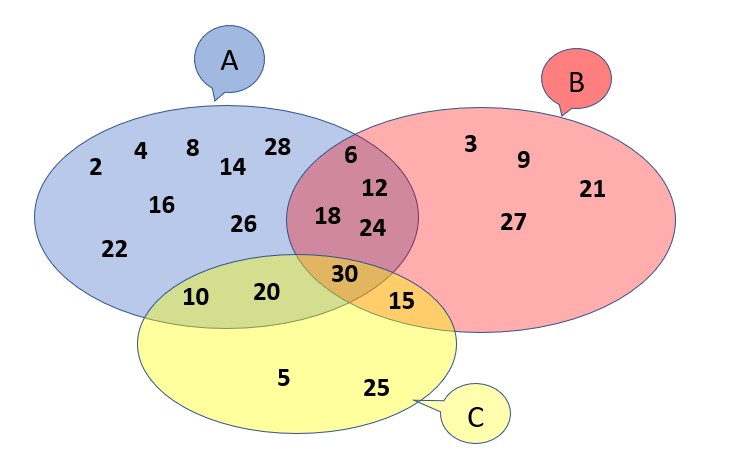
Réflexivité de l’intersection et de l’union :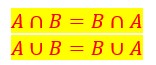
Associativité de l’union et de l’intersection :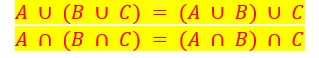
Distributivité de l’intersection par rapport à l’union :
Distributivité de l’union par rapport à l’intersection : 
Prenons 3 ensembles A,B,C définis ci-dessous :
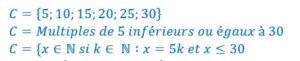
Les différentes intersections entre ces 3 ensembles sont :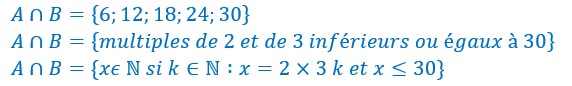
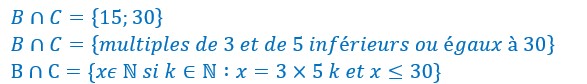
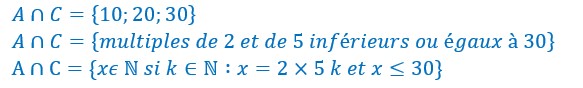
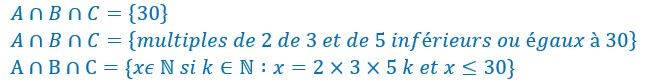
La réflexivité et l’associativité sont toutes deux évidentes.
On laisse le soin de vérifier les deux distributivités avec les éléments ci-dessus.
Cardinal d'un ensemble
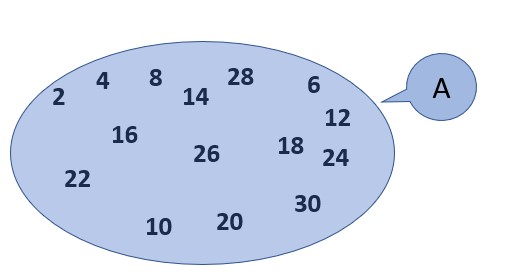
On appelle cardinal d’un ensemble fini A le nombre n d’éléments de cet ensemble. On note card(A)=n ou ΙAΙ=n
Si les ensembles sont disjoints :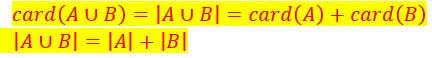 
Quel va être la cardinal de A union B ? 25 ?
Réfléchissons :
La réunion de ces deux ensembles présentent deux fois des éléments. Ce sont les éléments appartenant à la fois à A et a B, donc les éléments qui appartiennent à l’intersection des deux ensembles. Dans un ensemble, les éléments sont uniques et ne se répètent pas. Il faut donc soustraire une fois le nombre d’éléments appartenant aux deux ensemble, soit l’intersection. Or 
est constituée de 5 éléments. Donc : 
On en déduit la formule générale ci-contre.
Si les deux ensembles sont disjoints, il n’y a pas d’intersection. Donc le cardinal de l’intersection est égal à 0.
Produit cartésien
Définition du produit cartésien :
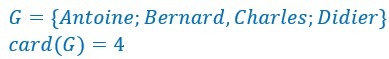
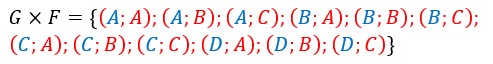
Produit cartésien de plusieurs ensembles :
Carré cartésien :
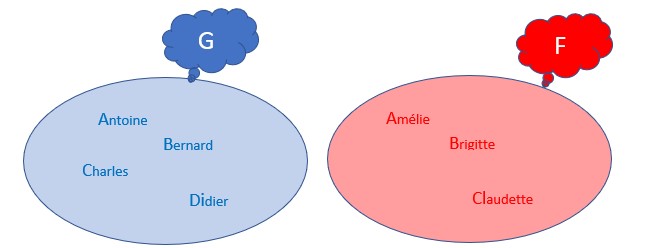
.Soit G un ensemble de 4 garçons et F un ensemble de 3 filles.
Avec ces deux ensembles on a la possibilité de former plusieurs couples.
Il s’agit de trouver la totalité des couples possibles à partir de ces deux ensemble et de les dénombrer.
On appelle produit cartésien l’ensemble de ces couples possibles. On écrit A X B. On lit A croix B.
On a reproduit ci contre ces deux ensembles et leur produit cartésien.
Dans un premier temps on a transcrit les prénoms en entier.
Comme le nombre de couples est relativement important et dépasse largement une ou deux ligne, nous n’avons utilisé que leur initiale.
Antoine a 3 choix possibles.
Bernard a également 3 choix possibles.
Charles aussi a 3 choix possibles.
Didier pareillement.
Ainsi on peut former 12 couples.
On peut noter la définition mathématique du produit cartésien ainsi que son cardinal.
Le produit cartésien d’un ensemble avec lui même est appelé carré cartésien.
On peut aussi imagniner un cube cartésien.
Permutations
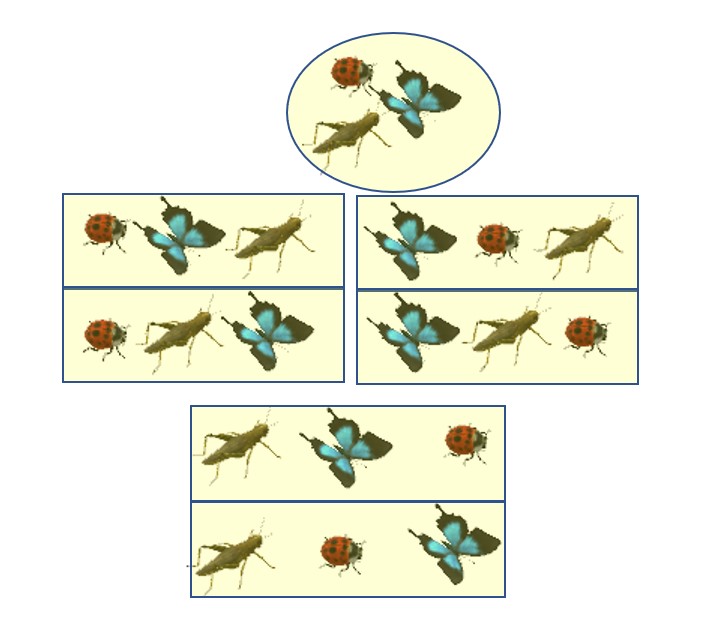
Léonore veut commencer une collection d’insectes qu’elle a trouvé dans le jardin de son grand-père. Pour l’instant, elle possède trois insectes : une coccinelle, un papillon et une sauterelle. Elle ne sait pas dans quel ordre elle va les épingler sur son carton. Elle hésite.
De combien de façon peut-elle les épingler ?
Si elle commence par la coccinelle, elle a ensuite deux manières d’épingler les deux autres : d’abord le papillon puis la sauterelle ou bien d’abord la sauterelle puis le papillon.
Si elle commence par le papillon, elle peut continuer soit par la coccinelle puis la sauterelle, soit par la sauterelle puis la coccinelle.
Si elle commence enfin par la sauterelle, elle épinglera ensuite soit le papillon puis la coccinelle, soit la coccinelle puis le papillon.
Pour épingler le premier insecte, elle a 3 choix possibles. Puis pour chacun de ses premiers choix, elle a 2 choix possibles, Enfin pour épingler le dernier insecte elle n’a qu’un choix.
On peut résumer tous ces résultats dans un tableau.
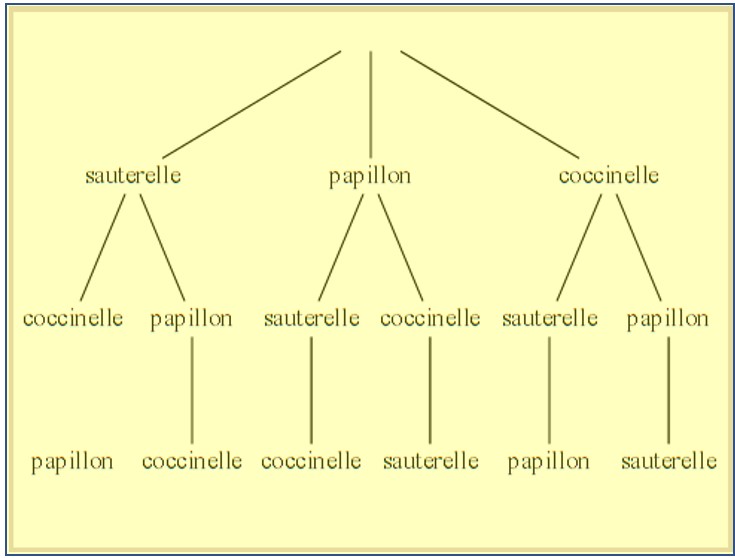
On peut aussi construire un arbre.
On note les premiers choix possibles.
Puis pour chacun de ces choix on note les deux choix possibles.
Enfin, on note le choix restant.
Ainsi Léonore a 3 X 2 X 1 : 6 possibilités pour épingler ses 3 insectes.
On peut aller plus loin :
si elle avait eu 4 insectes, elle aurait eu 4 X 3 X 2 X 1= 24 possibilités.
si elle avait eu 5 insectes, elle aurait eu 5 X 4 X 3 X 2 X 1= 120 possibilités.
On appelle ces différentes possibilités des permutations. On permute tous les termes de l’ensemble.
L’opération 5 X 4 X 3 X 2 X 1 représente le nombre 120 On note cette opération 5! qu’on lit factorielle 5 ou 5 factorielle.
Ainsi n! est le produit des nombres successifs de n jusqu’à 1 :
n!=n X (n-1) X (n-2) X ……(3) X (2) X(1).
On range les n éléments, tous les éléments de l’ensemble dans un certain ordre pour obtenir une permutation.
On dit aussi que la permutation d’un ensemble de n éléments est un n-uplet. Dans l’exemple de Léonore on a un 3-uplet (triplet).
Arrangements
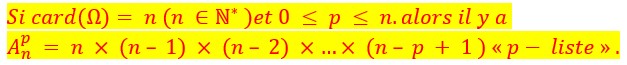
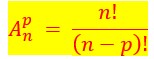Pour une course avec 25 chevaux, le nombre de tiercé ou de quinté possible est :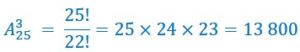
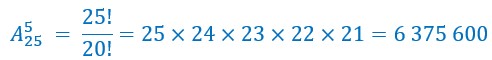
Mais le tiercé n’est pas tout à fait un jeu de hasard si on tient compte, de la forme du cheval, du jockey, des performances précédentes, en fait de nombreux facteurs pouvant intervenir
Néanmoins, il est dangereux de jouer à des jeux de hasard faisant intervenir l’argent.
Dans une course hippique, 10 chevaux sont en compétition.
Un tiercé est constitué du premier cheval arrivé , puis du deuxième et enfin du troisième.
(1;3;5) est un tiercé. Cela signifie que le cheval N° 1 est arrivé premier, le cheval N°3 est arrivé deuxième , le cheval N° 5 est arrivé troisième.
(5;1;3) est un autre tiercé. Les mêmes chevaux arrivent dans un ordre différent. Cette fois c’est le cheval N° 5 qui est arrivé premier , le N°1 deuxième et le n°3 troisième.
Parmi les 10 chevaux, je voudrais connaître le nombre de tiercés possibles.
Pour le cheval gagnant, celui qui arrive en premier, j’ai dix choix possibles.
Pour celui qui arrive deuxième, j’ai neuf choix possible, c’est à dire les 10 chevaux moins le cheval gagnant que j’ai choisi précédemment.
Pour celui qui arrive troisième, il me reste 8 choix .
Pour chaque choix du premier je peux choisir 9 chevaux et pour chaque choix du deuxième je peux en choisir 8.
Donc en tout j’aurai 10 X 9 X 8 =720 choix possibles.
On pourrait représenter tout cela par un arbre, mais ce serait trop difficile techniquement parlant (arbre ayant 10 branches, chacune des branches ayant 9 branches et chacune des 9 branches en ayant 8.)
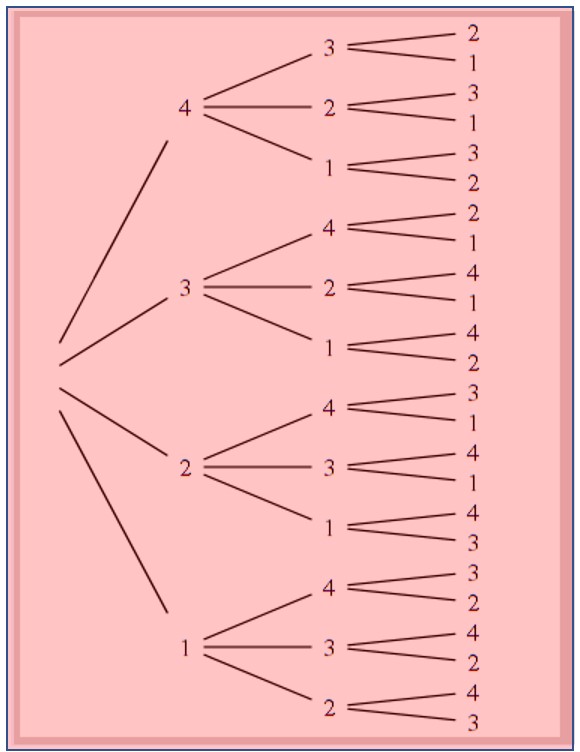
Construisons un arbre avec 4 chevaux au départ.
Dans ce cas on aura 4 X 3 X 2 = 24 possibilités.
Avec 4 chevaux, il s’agit de trouver toutes les listes ordonnées de 3 chevaux. {1;2;3}; {1;3,2};{3;2;1}…{2;3;4};{4;3;2]… Il y en a 24 (voir ci contre avec l’arbre.)
Avec 10 chevaux, il s’agit de même de trouver toutes les listes ordonnées de 3 chevaux. Il y en a 720.
Ainsi à partir d’un ensemble de chevaux de cardinal n, on construit toutes les p-listes ou tous les p-uplets ordonnés possibles. Dans le premier cas n=10 et p=3. On recherche trous 3-uplets ordonnés parmi 10 chevaux. En langage hippique c’et le tiercé.
Ces 3-listes ou 3-uplets sont appelés aussi arrangement. Ce sont tous les arrangements ordonnés de 3 chevaux parmi 10 chevaux.
En généralisant, on recherche le nombre de tous les arrangements de p éléments parmi un ensemble de n éléments. Ce qu’on écrit :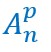 
On lit A-n-p
On aurait pu chercher le nombre de tous les 5-uplets parmi les 10 chevaux. C’est le quinté. Dans ce cas ou en aurait 10 X 9 X 8 X 7 X 6 = 30 240.
Remarque importante pour les calculs :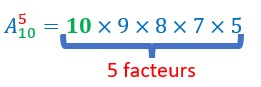 
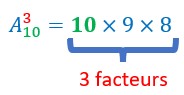
On peut remarquer aussi :
Combinaisons
Les arrangements de 3 chiffres parmi 4 :
En ne tenant pas compte de l’ordre, il reste uniquement les arrangements en rouge. Ce sont les 4 combinaisons de 3 chiffres parmi 4.
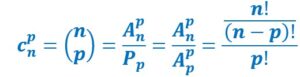
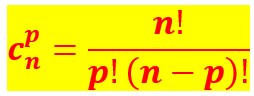
Après avoir joué au tiercé, on va jouer maintenant au loto.
On dispose de 49 numéros sous forme de boules ou de jetons.
Le jeu consiste à choisir 6 numéros parmi ces 49. L’ordre n’intervient pas. C’est-à-dire : {1;2;3;4;5;6} c’est pareil que {6;5;4;3;2;1}.
Combien a-t-on de possibilités de tirages de 6 numéros parmi 49 ?
Prenons un exemple plus simple dans un premier temps. Soit un ensemble de 4 éléments. Combien de combinaison a-t-on de 3 éléments parmi 4.
Dans le chapitre précédents nous avons vu que nous avions 24 arrangements possibles de 3 éléments parmi 4. Pour chacun des arrangements, il existe 3! =3 X 2 X 1= 6 permutations. Comme l’ordre ne compte pas, on ne conserve qu’une seule permutation de chaque arrangement. Donc on aura 24 :6 = 4 combinaisons.
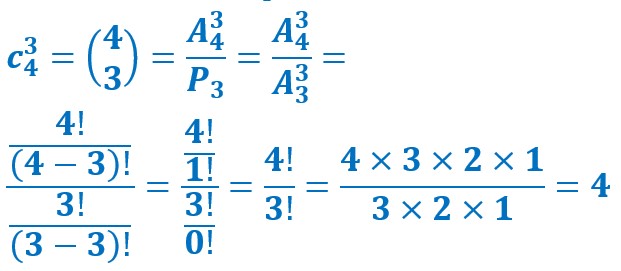
Deux notations sont équivalentes pour les combinaisons ;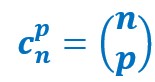 
Propriétés des combinaisons
Des formules à connaître sinon à savoir :
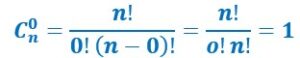
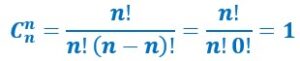
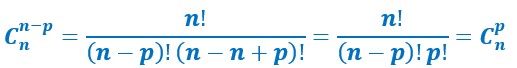
Formule de Pascal.
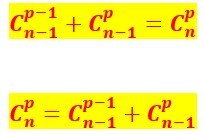
Cette formule lue dans un sens ou dans l’autre va servir pour construire le triangle de Pascal de proche en proche sans calculer chacune des combinaisons, ce qui serait fastidieux.
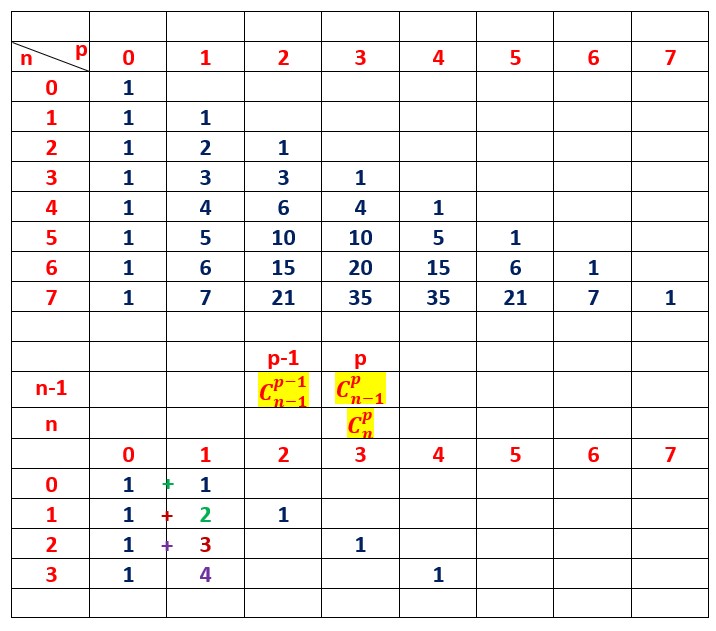
Pour construire ce triangle de Pascal, on met sur la première ligne tous les p de 0 à 7 ici.
On place dans la première colonne tous les n de 0 à 7.
Une cellule est définie par l’intersection de la colonne et de la ligne : (colonne; ligne) (n;p) représentant la combinaison de p éléments parmi n :
Puisque 
, on rempli la deuxième colonne de 1, Et puisque 
onremplitlescasesdeladiagonaleavecdes1.
Ensuite on additionne la cellule 1;0 avec la celle 1;1, ce qui donne 2 que l’on place dans la cellule 2;1.
puis de proche en proche (2:0)+(2;1)= 3 dans la cellule 3;1
(3;0)+(3;1)= 4 dans la cellule 4;1.
Et ainsi de suite.
On peut élaborer un triangle de Pascal avec des nombres plus grands. C’est très simple !
On calcule les deux premiers termes du premier membre de la première égalité.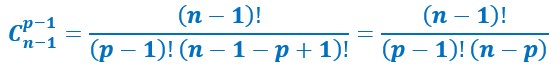 
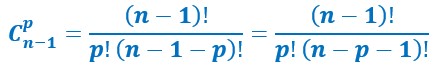
On les additionne pour obtenir le premier membre. On obtient dans le second membre deux fractions. (n-1)-p=n-p-1.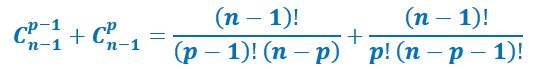
Pour additionner ces deux fractions, il faut les réduire au même dénominateur. Mais pour cela on va utiliser un autre stratagème : on multiplie le numérateur et le dénominateur de la première fraction par p, et on multiplie les numérateur et le dénominateur de la deuxième par (n-p).
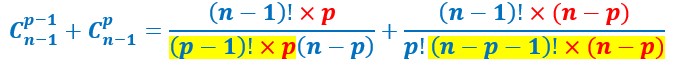
Or (p-1)! x p est égal à p!. (4-1)! x 4= 3! x 4= 3x2x1x4=4x3x2x1=4!.
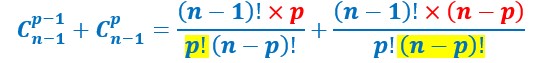
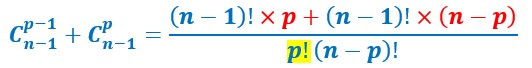
On factorise par (n-1) :
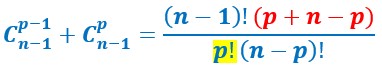
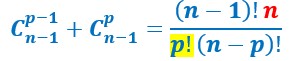
Or (n-1)!n=n!
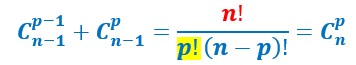
La démonstration est terminée.
Binôme de Newton
Formule du binôme de Newton :
Ce qui signifie : (a+b) puissance n égal somme de p=0 à p=n des 
Voyons ce que cela donne avec la puissance 7 :
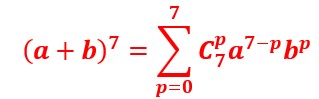
En développant cette formule on obtient (attention, il faut être très concentré ) :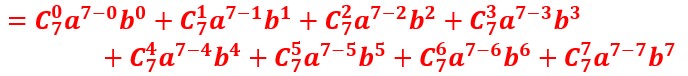
soit :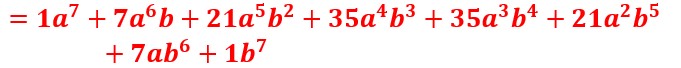 
Il faut bien sûr éliminer les deux 1 inutiles.
Tout le monde a appris en quatrième la première identité remarquable :
que l’on peut écrire en notant les coefficients devant chacun des termes :
On remarque que ces coefficients sont les ceux de la ligne 2 du triangle de Pascal.
On peut donc écrire :
Voyons si cela fonctionnerait avec (a+b)3.
Il suffit de distribuer. Autrefois on apprenais les identités remarquables du troisième degré. 
soit :
Miracle ce sont les coefficients de la ligne 3 du triangle de Pascal :
On pourrait continuer ainsi et on obtiendrait la formule du binôme de Newton ci contre. On peut utiliser une démonstration par récurrence.
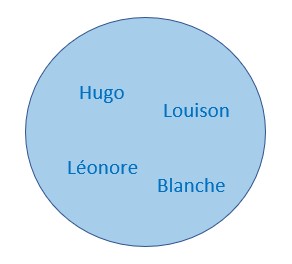
Nombre de parties d'un ensemble
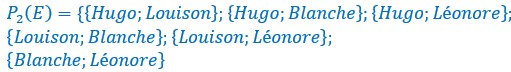
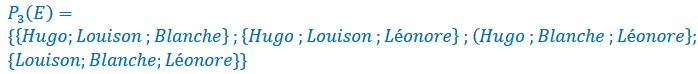
Maman veut emmener ses 4 enfants aux commissions. Elle sait qu’ils vont se battre pour occuper les sièges de la voiture.
Voyons les possibilités sachant qu’on ne tient pas compte de l’ordre, autrement dit on ne tient pas compte du fait que l’enfant soit à gauche ou à droite, au milieu ou près d’une fenêtre.
Aucun enfant n’a envie d’aller aux commissions. Aucun enfant ne monte dans la voiture.
C’est le choix de 0 élément parmi 4.
Finalement après des palabres, tout le monde veut partir mais ils se battent pour occuper le siège avant.
C’est le choix de 1 élément parmi 4.
Le problème du siège avant n’est pas résolu mais on se bat pour occuper les deux sièges arrières.
C’est le choix de 2 éléments parmi 4.
Pour les trois sièges du milieu, c’est le choix de 3 éléments parmi 4.
Il reste une possibilité : Hugo qui a le parmi emmène ses 3 soeurs et laisse maman à la maison.
Ainsi le nombre de parties que l’on peut établir avec cet ensemble de 4 éléments est-il égal
Au nombre de parties à 0 éléments + le nombre de parties à 1 éléments + le nombre de parties à 2 éléments + le nombre de parties à 3 éléments + le nombre de parties à 4 éléments.
On admettra que ce nombre est égal à 24.
Applications , fonctions.
Un exemple d’application :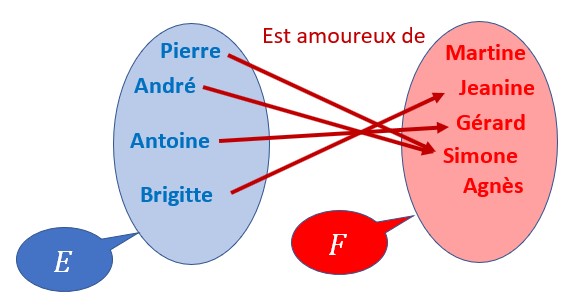
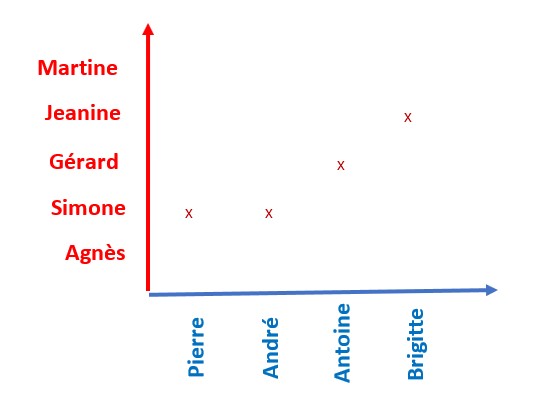
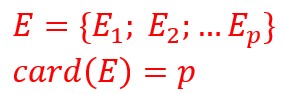
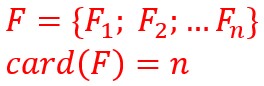
E1 a n images possibles F1;F2……Fn
E2 a n images possibles F1;F2……Fn
……
Ep a n images possibles F1;F2……Fn.
Une image de E1 avec une image de E2….. avec une image de Ep donne une application.
On aura donc en tout n x n x …….x n (p fois) applications soit np applications.
Faisons une petite incursion dans la vie amoureuse des femmes et des hommes pour essayer d’expliquer ce qu’est une application.
Soit un ensemble E dont les éléments sont des femmes et des hommes représentés par leur prénom. On appelle cet ensemble ensemble de départ.
Soit un ensemble F dont les éléments sont aussi des hommes et des femmes représentées par leur prénoms.
On définit une relation f entre ces deux ensembles; On a choisi ici la relation est amoureux de.
A chacun des éléments de l’ensemble de départ E correspond un élément de l’ensemble d’arrivée F.
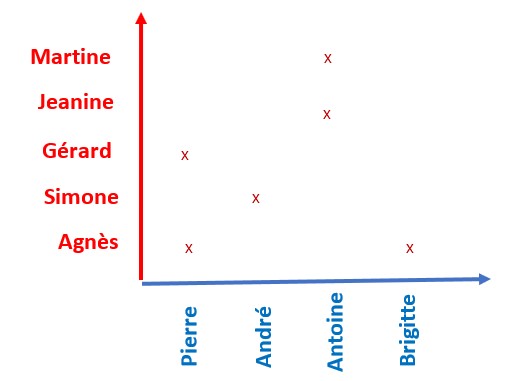
On obtient ainsi des couples. Dans l’application ci-contre, les couples sont les suivants :
{Pierre; Simone}, {André; Simone},
Antoine; Gérard},{Brigitte; Jeanine}.
On dit que chaque élément de E possède une image dans F.
L’image dans F a un antécédent dans E.
Chacun des éléments de E est pris en compte. Autrement dit à tous les éléments de E correspond un élément de F. Tous les éléments de E ont une image dans F.
Mais nous constatons que chaque élément de F n’a pas forcément d’antécédent dans E.
A chaque prénom de E il part une flèche et une seule.
A chaque éléments de F arrive zéro ou plusieurs flèches.
Cela est théorisé par la définition des applications ci-contre en rouge surlignée de jaune.
On a représenté un exemple d’application où Pierre est amoureux de Simone. Mais il pourrait bien être amoureux de Jeanine ou de Gérard ou d’Agnès. IL est est de même pour André qui pourrait bien être amoureux de Martine ou Jeanine ou Gérard ou Agnès et ainsi de suite pour tous les autres.
Chaque fois on obtient une nouvelle application.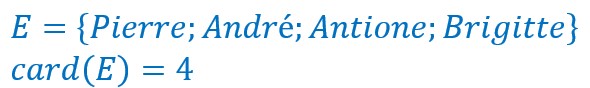 
Ainsi Pierre a-t-il 5 images possibles, il peut être amoureux de 5 personnes différentes de l’ensemble F.
André a également 5 images possibles.
Antoine a aussi 5 images possible.
Brigitte également 5 images possible.
Une image de Pierre + une image d’André + une image d’Antoine + une image de Brigitte constituent une application.
On aura donc 5 x 5 x 5 x 5 x 5 = 54 applications différentes .
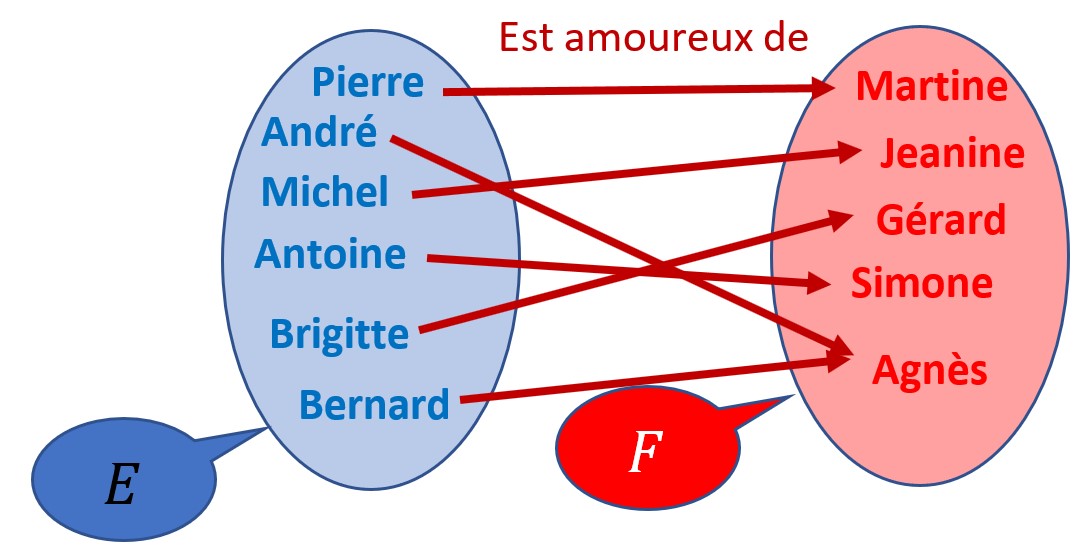
Ceci n’est pas une application :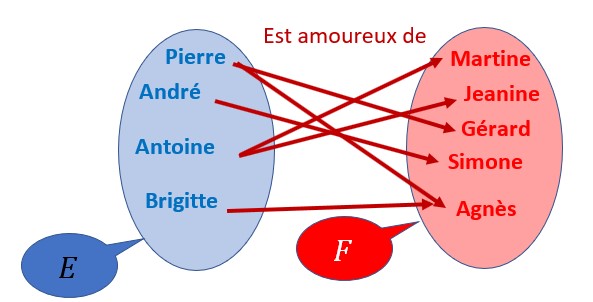
On voit que Pierre a deux images dans F , Gérard et Agnès. Pierre est amoureux de deux personnes. C’est son droit !
Il en est de même pour Antoine : Martine et Jeanine.
De certains éléments de l’ensemble de départ, il part deux flèches.
Ce n’est pas une application. Car dans une application, chacun des éléments de l’ensemble de départ ne doit avoir au plus qu’une image et une seule.
Dans ce cas, il est impossible de trouver le nombre de relations pouvant exister entre l’ensemble de départ et l’ensemble d’arrivée.
Ceci est une fonction :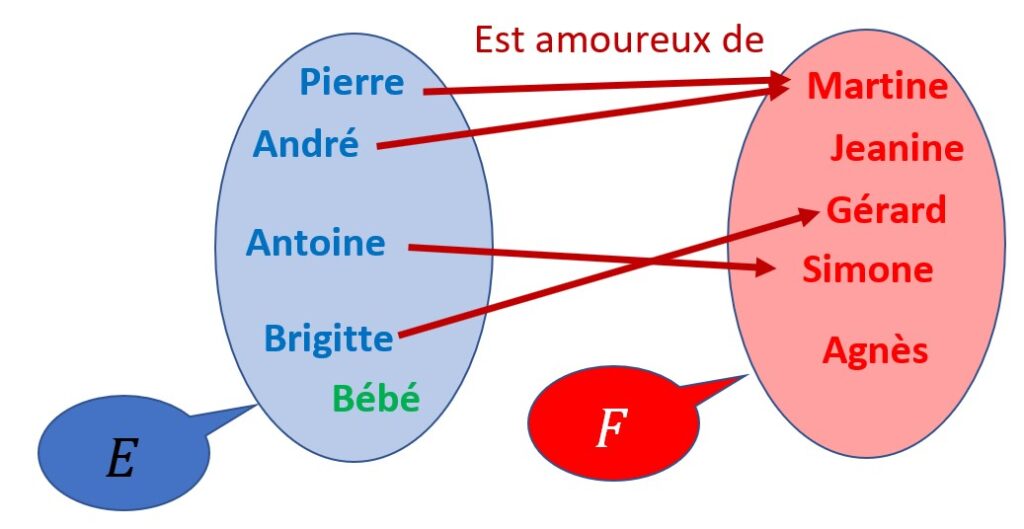
Injection, surjection, bijection.
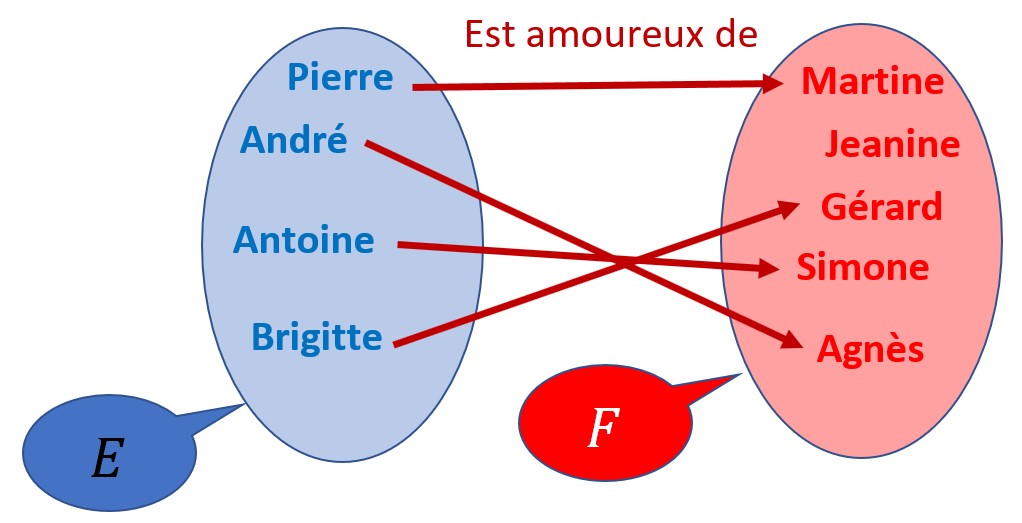
La relation ci-contre est une application. En effet, chaque élément de l’ensemble de départ E possède une image.
Cette application est une injection car chaque élément de l’ensemble d’arrivée F possède au plus un antécédent, c’est-à-dire zéro ou un antécédent.
Si on prend la définition : il est évident que dans ce cas si Gérard=Gérard alors Brigitte = Brigitte.
Si on prend la première assertion :
Gérard différent de Simone alors Brigitte différend d’Antoine.
On représenté ci-contre une des injections possibles parmi toutes.
Nombre d’injections.
Pierre a 5 choix possible.
Une fois ce choix effectué, l’objet de son choix ne peut pas être choisi par un autre; S’il choisit Martine, Martine ne pourra pas être choisie ensuite. Si non ce n’est plus une injection.
Donc André n’aura que 4 choix possible.
Antoine en aura 3 et Brigitte 2.
Donc on aura 5 x 4 x 3 x 2 injection : c’est le nombre d’arrangements de 4 éléments parmi 5.
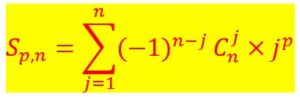
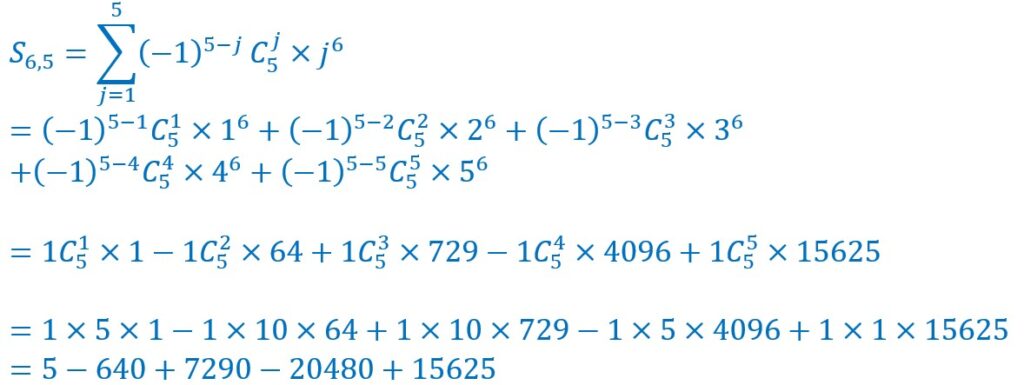
Exemple de bijection :
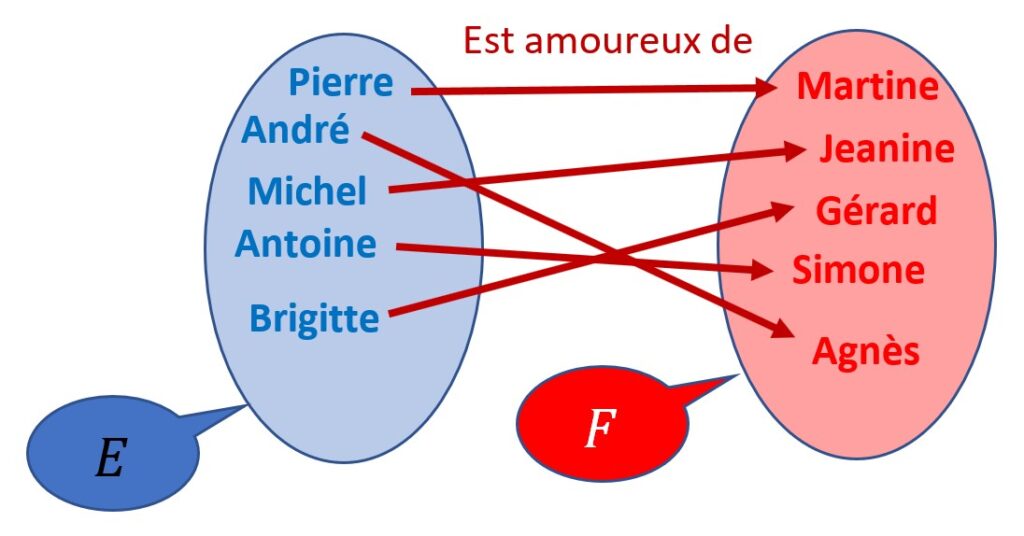
Une application est une bijection si tous les éléments de l’ensemble d’arrivée F possèdent un et un seul antécédent dans l’ensemble de départ E.
Ainsi les cardinaux des ensembles de départ et d’arrivée sont-ils égaux.
Pour calculer le nombre de bijections :
Pierre a n choix possible.
Une fois le choix de Pierre effectué, André a n-1 choix possible (n choix moins le choix de Pierre)
Michel aura n-2 choix possible.
et ainsi de suite.
Le nombre de bijection sera donc égal à n!.
Soit g l’application réciproque de l’application f.
L’ensemble de départ est cette fois l’ensemble F et l’ensemble d’arrivée, l’ensemble E. L’application devient “est aimé par”.
Martine est aimé par Pierre.
Jeanine est aimée par Michel
Gérard est aimé par Brigitte ….
Si on compose les deux applications, dans un sens ou dans l’autre on obtient l’application identique.
Exemple :
Pierre est amoureux de Martine composée avec Martine est aimée de Pierre. En partant de Pierre on arrive à Pierre.
Martine est aimée de Pierre composée avec Pierre est amoureux de Martine. En partant de martine, on arrive à Martine.
Résumé
