Groupes
Définitions
Structure
Structure est un nom féminin qui vient du latin struere signifiant “bâtir”.
Manière dont un édifice est bâti.
Manière dont les différentes parties d’un objet sont disposées les unes relativement aux autres.
Synonymes : ordre, arrangement, disposition, organisation, agencement.
En mathématiques :
Ensembles possédant une ou plusieurs lois de composition
Loi de composition
Exemples de lois de composition internes :
L’addition dans les ensembles 
:
3 € 
; 2 € 3+2=5
(-3) € 
; (-2) € (-3)+(-2)=(-5) € 
3,14 € 
2,718 € 3,14+2,718=5,858 €
3+2i € 
4+7i € (3+2i)+(4+7i) =7+9i €
La multiplication dans
La soustraction dans 
La division dans 
Multiplication des matrices.
Composition des fonctions.
Exemples de lois de composition externe :
Exponentiation entière des réelle : 
Bien sûr on peut prendre des exposants négatifs, fractionnaires mais aussi réels et dans ce dernier cas on a une loi de composition interne.
La multiplication d’un vecteur appartenant à un espace vectoriel E par un scalaire.
Une loi de composition désignée par le symbole * : E × F → G, avec G = E ou G = F, est une application de E × F dans G (soit E, soit F) qui associe à chaque couple ( x, y ) de E × F, un élément de G noté habituellement « x * y » et appelé composé de x et de y, ou encore produit de x et y.
On prend un élément x appartenant à l’ensemble E : x € E
On prend un élément y appartenant à l’ensemble F : y € F
On dit aussi que le couple (x;y) appartient à E X F (E croix F) : (x;y) € EXF
On fait subir à ce couple d’éléments une ou plusieurs opérations de telle façon qu’on obtienne un troisième élément z appartenant soit à E soit à F.
L’opération appliquée à x et y est appelée * (étoile).
On peut écrire (x*y) € E ou F.
x et y sont parfois qualifiés d’opérandes.
si E = F = G, la loi * : E × E → E est appelée loi de composition interne dans E ;
si E ≠ F et G = F, la loi * : E × F → F est appelée loi de composition externe à gauche sur F ou loi de composition externe, et E est alors le domaine des opérateurs ;
si E ≠ F et G = E, la loi * : E × F → E est appelée loi de composition externe à droite sur E de domaine F.
Groupe
Soit un ensemble 
Soit une loi de composition notée 
. C’est une loi quelconque qui n’a rien à voir avec l’addition. On compose deux éléments 
et 
de l’ensemble et la composition de ces deux éléments donnent un troisième élément appartenant à l’ensemble
La loi est associative : cela veut dire que pour est un élément de est un élément de 
est un élément de
si on compose par la loi les deux premiers et et ensuite le résultat avec le troisième on obtient le même résultat en composant le premier avec la composition des deux autres et .
La loi possède un élément neutre : Si on compose n’importe quel élément de l’ensemble on obtient à nouveau l’élément .
Tout élément de l’ensemble possède un symétrique : si on compose deux éléments symétriques de l’ensemble , on obtient l’élément neutre 
.
Cela semble compliqué, oui car la formulation est abstraite pour qu’elle puisse s’appliquer en général, mais nous allons voir par des exemples ci-contre que c’est finalement très simple.
Un groupe est un ensemble muni d’une loi de composition interne.
Cette loiest associative 
elle possède un élément neutre 
tout élément de l’ensemble possède un symétrique 
L’ensemble des entiers naturels muni de la loi d’addition que l’on connaît + est un groupe.
L’ensemble des entiers naturels est ayant une infinité d’éléments : ….. -1000…….-4;-3;-2;-1;0;1;2;3;4…..1000….
Loi de composition interne : Si on additionne deux quelconques nombres de cet ensemble, on obtient en résultat un entier naturel.
3+1=4 (-3)+(-1)=-4
Elément neutre : Si on additionne n’importe quel nombre de l’ensemble des entiers naturels avec l’élément 0, on obtient ce même entier naturel :
3+0=3 2023+0=2023
-3+0=-3 -2023+0=-2023
Symétriques : Chaque élément de l’ensemble des entiers relatifs possède un symétrique appelé opposé.
6 a pour opposé -6 6+(-6)=0
L’ensemble des entiers naturels muni de l’addition n’est pas un groupe. En effet il n’existe pas de symétrique appartenant à cet ensemble.
Par contre l’ensemble des entiers naturels muni de la multiplication est un groupe. L’élément neutre est 1 et chaque élément de cet ensemble possède un symétrique appartenant à cet ensemble. 2 et 1/2 par exemple. Ce symétrique se nomme l’inverse.
Groupe abélien
Un groupe abélien est un groupe dont la loi interne possède les mêmes propriétés que celle d’un groupe simple mais en plus elle est commutative. Cela signifie que l’on peut composer les éléments dans n’importe quel ordre.
1+2=2+1=3
Un groupe abélien ou groupe commutatif est un ensemble muni d’une loi de composition interne.
Cette loi est associative
elle est commutative 
elle possède un élément neutre
tout élément de l’ensemble possède un symétrique
Exercices
L’ensemble des nombres réels muni de la loi tel que 
est-il un groupe ?
- la loi est une loi de composition interne . En effet quels que soient x et y appartenant à l’ensemble des réels leur somme x+y est un réel, leur produit xy est aussi un réel et la différence entre leur somme et leur produit est un réel. Ce qu’on peut écrire en langage mathématiques :
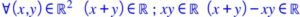
Cette loi consiste à opérer ainsi : premier nombre plus deuxième nombre moins le produit des deux. - Associativité : a-t-on
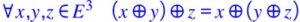
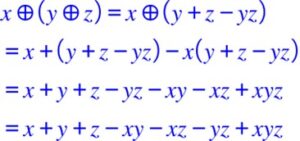
On a bien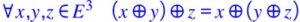 - Elément neutre :
Il faut :
Trouvons cet élément neutre s’il existe.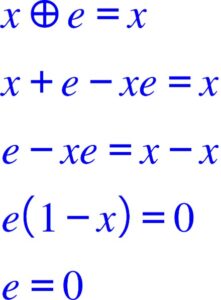
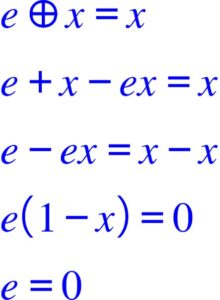
- Elément symétrique. Soit x’ cet élément de x quelconque appartenant à l’ensemble des réels. S’il existe il vérifie
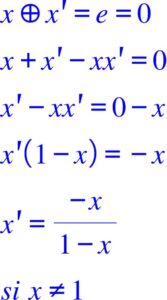
On trouve le même résultat avec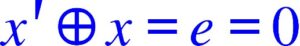
Comme il n’existe un symétrique que pour les valeurs de x différentes de 1. Il n’y a donc pas de symétrique pour tout x.
Nous en déduisons que l’ensemble muni de la loi n’est pas un groupe. 
n’est pas un groupe.
L’ensemble des rotations de centre O muni de la loi de composition des rotations 
est-il un groupe ?
La loi est une loi de composition interne. En effet une rotation de centre O et d’angle θ suivit d’une rotation de centre O et d’angle θ’ revient à faire une rotation de centre O et d’angle θ+θ’.
La loi est associative :
On obtient le même résultat final dans les deux opérations suivantes
1-On compose une rotation O d’angle θ avec une (rotation O d’angle θ’ composée avec une rotation O d’angle θ”).
2-On compose (une rotation O d’angle θ composée avec une rotation O d’angle θ’) avec une rotation O d’angle θ”.
Elle possède un élément neutre.
C’est la rotation O d’angle θ=0.
Une rotation O d’angle θ suivie d’une rotation O d’angle 0 revient à n’effectuer que la rotation O d’angle θ.
Eléments symétriques
Toute rotation O d’angle θ possède une rotation symétrique, la rotation O d’angle -θ.
En plus
Elle est commutative
On obtiendra le même résulta si on commence par la Rotation O d’angle θ pour finir la rotation O d’angle θ’ ou inversement si on commence par la rotation O d’angle θ’ pour finir par la rotation O d’angle θ.
Dans l’animation ci-dessous :
C’est un manège d’enfants ayant une voiture de pompiers.
pour l’associativité On clique sur le bouton bleu Rθ le camion de pompier tourne d’un angle de 30° puis on clique sur le second bouton bleu, le camion tourne de 20° supplémentaire en tout il aura tourné de 50°
On initialise pour ramener le camion à l’origine de son déplacement.
On clique successivement sur les boutons bleus en dessous.
Après initialisation on opère de même pour toutes les aurtes propriétés.