Le cercle trigonométrique
- par gabriel
- dans Mathématiques, Trigonométrie
- sur 5 septembre 2019
Cercle orienté
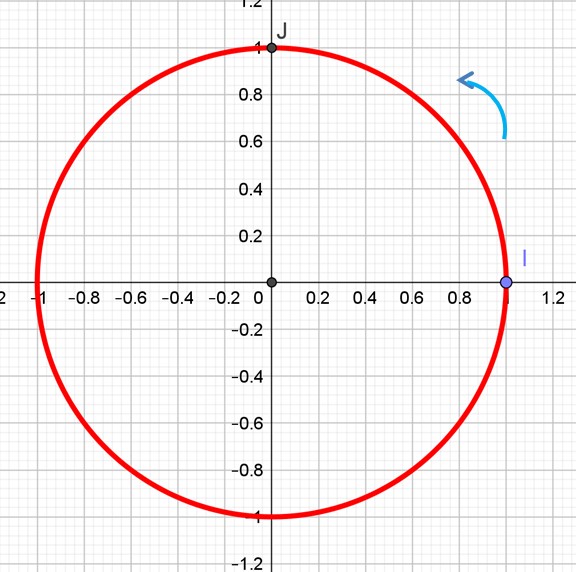
C’est un cercle de rayon 1 : R=1 unité
Cette unité peut être le cm, le m ou tout simplement l’unité.
Nous savons que la longueur du cercle, ou le périmètre du cercle, le parcours que je fais en partant de I, en suivant le cercle ( la piste ) pour revenir à I est égal à ![]()
2 fois π multiplié par le rayon.
π vaut environ 3,14 unités.
Sur un cercle trigonométrique on tourne dans le sens inverse des aiguilles d’une montre. C’est le sens positif . C’est le sens trigonométrique. On dit parfois le sens direct.
Si on tourne dans le sens des aiguilles d’une montre c’est le sens négatif.
Ce parcours de 1 tour complet représente un arc de cercle (en fait le cercle entier) de 360° (degrés) ou 400 gr (grades) ou 2 π rad (Radians)![]()
et 
et 

Repérage d'un point sur le cercle
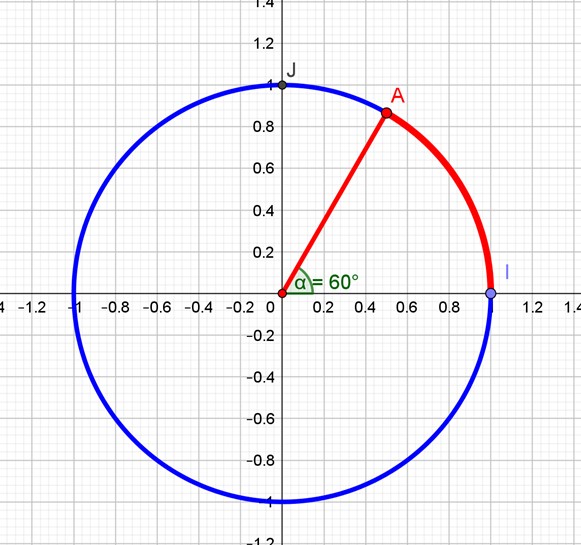
La mesure de l’angle IOA est la même que la mesure de l’arc IA, ici 60°
car l’angle IOA est un angle au centre son sommet étant le centre du cercle.
La mesure de l’angle au centre est égale à la mesure de l’arc qu’il intercepte sur le cercle.
Le point A peut être repérer sur le cercle à partir du point I en mesurant l’angle IOA ou l’arc IA.


Pareillement le point B est repéré sur le cercle à partir du point I.![]()
Le point C est aussi repéré sur le cercle à partir du point I grâce à l’angle ou à l’arc.
Mais attention cette fois, on part de I pour aller vers C. On tourne dans le sens des aiguilles d’une montre, dans le sens inverse au sens trigonométrique ou sens directe. L’angle ainsi décrit est négatif. On l’indique par le signe moins devant la mesure de l’angle.
Quelques points particuliers
En partant de I vers J sens positif lire les angles rouges
Je pose mon crayon sur le point I, en suivant le cercle, je glisse vers J, je m’arrête dès que je trouve un point et je lis la mesure en rouge, je continue et m’arrête à nouveau dès que je trouve un point ……
En partant de I vers J’, sens négatif lire les angles bleus.
Je pose mon crayon sur le point I, en suivant le cercle, je glisse vers J’, je m’arrête dès que je trouve un point et je lis la mesure en bleu, je continue et m’arrête à nouveau dès que je trouve un point ……




Conversions
Comment passer d’une unité à l’autre ? Comment convertir des degrés en radians et vice versa ? On laisse les grades de côté.
On peut utiliser la règle de trois ou un tableau de proportionnalité.
Convertir des degrés en radians
On sait que 180° correspond à π radians.
On dispose ces chiffres dans la colonne « je sais que ».
On doit convertir 60° en x radians.
on dispose ces termes dans la colonne « données ».

On effectue le produit en croix.
On obtient une équation en x qu’il faut résoudre.
On laisse le symbole π
On obtient la valeur de x en radians en fonction de π.

Si on veut la valeur de x en radians sans π, il suffit de remplacer π par sa valeur et d’effectuer l’opération.

Convertir des radians en degrés.
On peut faire de la même façon, avec un tableau de proportion.
On laisse les π et on les simplifie.

Mais on peut faire plus simple.
On sait qu’un angle de π radians correspond à 180°. Il suffit de remplacer π par 180 et le tour est joué.
Mais attention, attention, π n’est pas égal à 180° (Il est égal à 3,14 environ) C’est la raison pour laquelle on n’a pas mis de signe égal mais une flèche qui signifie π correspond à un angle de 180 °

Mesure principale d'un angle
Pour un même angle, il existe une infinité de mesures.

En partant du point I qui est l’origine des angles, je m’arrête en A. J’ai parcouru un arc de 60°, j’ai balayé un angle IOA de 60° = π/3 rad. C’est la mesure principale de l’angle.
Mais arrivé en A, je peux continuer, faire le tour du cercle pour revenir en A. Ainsi j’aurai en plus de mon arc IA fait un tour complet :
Arc IA + 1 tour
Or un tour est égal à 2π radians et l’arc IA mesure π/3 radians.
Donc j’ai parcouru en tout π/3 + 2π radians.
Si j’effectue un tour supplémentaire car je me trouve en forme, j’aurai parcouru
π/3 +2 fois 2π= π/3 + 2 x 2π
Aller je fais 3 tours : π/3 + 3 x 2π
Si je fais k tours : π/3 + k x 2π k étant un entier compris entre -∞ et +∞ :]-∞;+∞[.
Avec un tour complet k=1, mon angle mesure 
Avec deux tours complets, k=2

Un angle orienté peut s’exprimer d’une infinité de manière (suivant le nombre de tours, soit le nombre de fois 2π), La mesure principale de cet angle est celle qui est comprise dans l’intervalle ]-π;π[.
Nous allons voir comment trouver la mesure principale d’un angle

π![]() est plus grand que 1 car le numérateur est supérieur au dénominateur.
est plus grand que 1 car le numérateur est supérieur au dénominateur.
 est donc supérieur à π et ne se trouve pas dans l’intervalle ]-π;π]. Ce n’est pas une mesure principale.
est donc supérieur à π et ne se trouve pas dans l’intervalle ]-π;π]. Ce n’est pas une mesure principale.
Il faut soustraire un certain nombre de tour k x 2π ou 2kπ
Le 6kπ plus proche de 5π est pour k = 1 donc 6π
On vient d’obtenir la mesure principale.Il ne reste plus qu’à placer le point sur le cercle
En utilisant le compas et la règle, on partage le demi cercle en 3 parties égales. Pour ce partage particulier, c’est simple, il suffit de reporter sur le cercle l’écartement du compas égal au rayon du cercle.
Comme notre angle est négatif, on reporte dans le sens inverse.


On procède de la même façon, on enlève un certain nombre k de 2π, pour s’approcher au plus près de cette valeur.

On réduit au même dénominateur

On cherche mentalement la valeur de k qui permettra d’être au plus près de notre angle initial.
Ici k= 4.



On procède presque de la même façon sauf que :
l’angle étant négatif, au lieu de soustraire un certain nombre k de 2π, on les ajoute.


Il est évident que k = 10.

Angles orientés, vecteurs
Il est possible évidemment de mesurer un angle orienté sans le recours du cercle trigonométrique.
Il existe deux manières pour désigner un angle.
Celle qui utilise la notation traditionnelle des angles.
Le cercle trigonométrique n’est pas tracé, mais on peut imaginer dans quel sens on tourne.



Celle qui utilise la notation vectorielle des angles, les côtés des angles étant des vecteurs.



Attention autre façon



Pour aller plus loin : animation sur les fonctions trigonométriques :
Cosinus et sinus
Pour démarrer l’animation, cliquer sur la petite flèche « Démarrer/Arrêter » en bas à gauche.
Ci contre un cercle dont le rayon est égal à une unité (ce peut être le cm, le dm, le m …..).
Le point B parcours le cercle dans le sens trigonométrique (inverse des aiguille d’une montre)
En se déplaçant sur le cercle, le point B balaye un angle α mesuré en radians.
On projette le point B sur les axes des abscisses et des ordonnées, respectivement en C et en A.
La longueur OC est le cosinus de l’angle α indiquée par l’abscisse C du point B.
La longueur OA est le sinus de l’angle α indiquée par l’ordonnée A du point B.
On peut cliquer sur le point B et le déplacer avec la souris suivant le cercle.
Tangente
Dans l’animation ci-contre, la tangente de l’angle α est donnée par la longueur du segment ΩT et l’ordonnée du point T écrite entre parenthèse, son abscisse étant 1.
On a tracé une droite tangente en Ω au cercle trigonométrique de centre O et de rayon égal à une unité.
En cliquant sur la petite flèche « Démarrer/Arrêter en bas à gauche de l’animation, le point B se déplace sur le cercle dans le sens trigonométrique ( inverse des aiguille d’une montre) .
La droite OB coupe la tangente au cercle au point T .
La longueur ΩT est la valeur de la tangente de l’angle ΩOB.
On peut arrêter et rétablir l’animation en cliquant sur la petite flèche Démarrer/Arrêter.
On peut aussi pointer le point B avec la souris et le faire déplacer sur le cercle en bougeant la souris.
Pour un angle α compris entre 0 et π/2 la valeur de la tangente est positive.
Pour α égal à π/2 la droite OB est parallèle à la tangente. Ces deux droites se coupent donc à l’infini. La valeur du segment ΩT est indéfini.
De π/2 à π La valeur de la tangente est négative.
De π à 3π/2 elle est positive
De 3π/2 à 2π elle est négative.
Cotangente
Sur l’animation ci-contre, on a représenté la cotangente dont la valeur est l’inverse de la tangente. En fait c’est la tangente du complémentaire de l’angle α.
Cette cotangente est représentée par la longueur du segment A1T’.
Sur l’animation la tangente et la cotangente varient conjointement en fonction de la valeur de l’angle α.
On n’utilise que très peu cette fonction trigonométrique.