Les quadrilatères
Quadrilatère quelconque
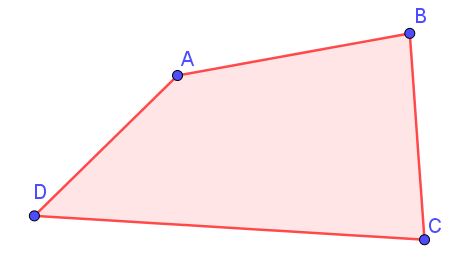
Un quadrilatère est un polygone (poly = nombreux gone = angle) possédant 4 côtés et donc 4 angles.
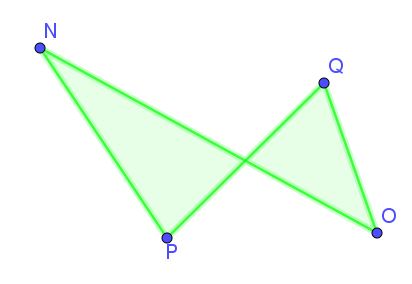
Il peut être droit ou croisé.
Ils possèdent des droites particulières
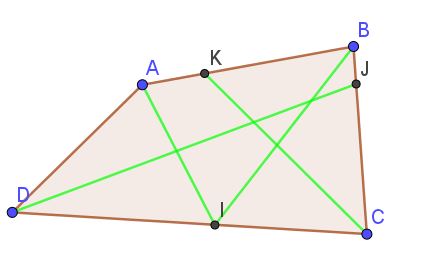
Deux diagonales qui joignent les sommets opposés.
Deux médianes qui joignent les milieux des côtés opposés.
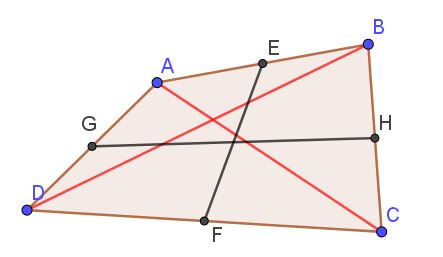
Quatre bissectrices qui partagent chacun des quatre angles en deux angles égaux.
Le parallélogramme
Définition :
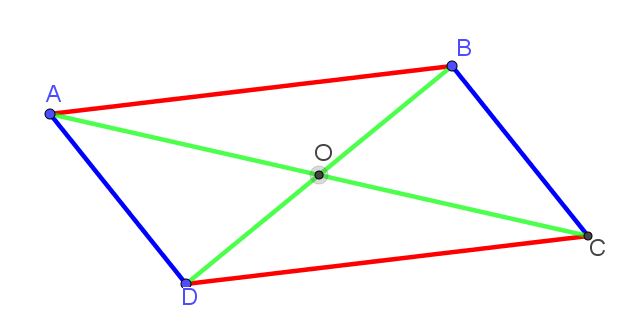
Un parallélogramme est un quadrilatère dont les côtés opposés sont parallèles.
AB parallèle à DC et AD parallèle à BC
Propriétés :
Ses côtés opposés sont égaux :
AB = DC et AD = BC
Ses diagonales se coupent en leur milieu :
OA = OC et OB = OD
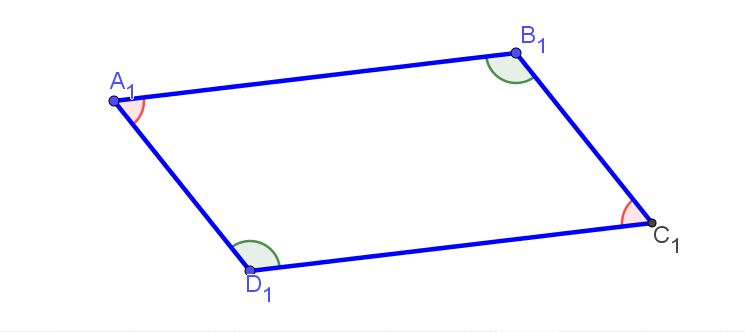
Ses angles opposés sont égaux :
Ses angles consécutifs sont supplémentaires, leur somme est égale à 180°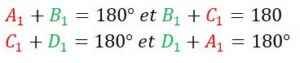
Le point O est centre de symétrie du parallélogramme
Pour démontrer qu’un quadrilatère est un parallélogramme, il faut démontrer l’une des affirmations suivantes :
Ses côtés opposés sont parallèles
Ses côtés opposés sont égaux.
Deux côtés opposés sont à la fois parallèles et égaux.
Ses diagonales se coupent en leur milieu.
Ses angles opposés sont égaux.
Périmètre et Aire (Surface)
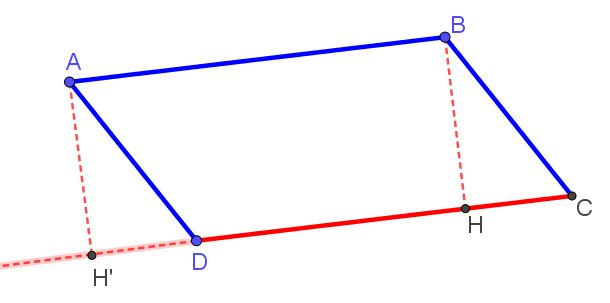
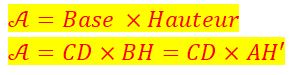
On peut construire la hauteur relative à n’importe quel côté.
Le rectangle
Définitions
Le rectangle est un quadrilatère qui possède 3 angles droits. Si un quadrilatère possède trois angle droits, il en possède obligatoirement 4 puisque la somme des angles d’un quadrilatère est de 360 °
Le rectangle est un parallélogramme qui possède 1 angle droit.
Propriétés :
Il possède toutes les propriétés du parallélogramme.
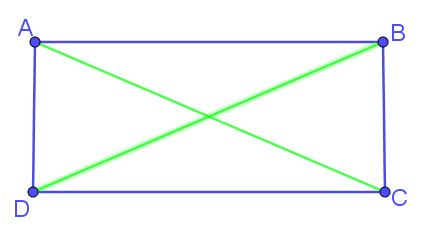
Ses diagonales AC et BD sont égales.
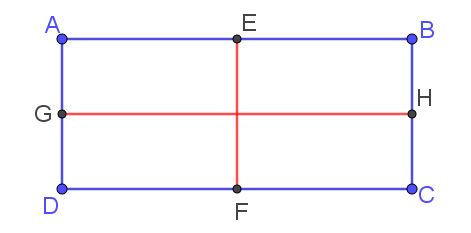
Ses deux médiatrices EF et GH sont deux axes de symétrie.
Pour démontrer qu’un quadrilatère est un rectangle, il faut démontrer l’une des affirmations suivantes :
C’est un quadrilatère qui possède 3 angles droits.
C’est un parallélogramme qui possède un angle droit.
C’est un parallélogramme dont les diagonales sont égales.
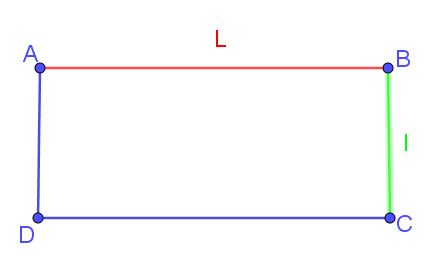
Périmètre et Aire
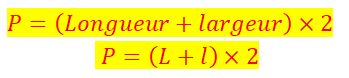
Le Losange
Définitions
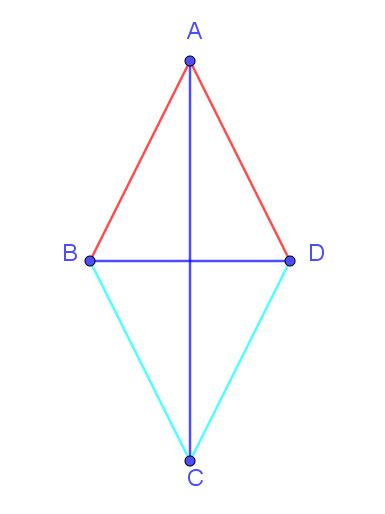
Le losange est un quadrilatère qui possède 4 côtés égaux.
AB=BC=CD=DA
Le losange est un parallélogramme qui a deux côtés consécutifs égaux.
AB=AD ou BC=DC
Propriétés
Il possède toutes les propriétés du parallélogramme
Ses diagonales sont perpendiculaires.
Ses diagonales sont deux axes de symétrie.
Ses diagonales sont bissectrices des angles aux sommets.
Pour démontrer qu’une figure est un losange, il faut démontrer l’une des affirmations suivantes:
C’est un quadrilatère qui possède 4 côtés égaux.
C’est un parallélogramme qui possède deux côtés consécutifs égaux.
C’est un parallélogramme dont les diagonales sont perpendiculaires.
Périmètre et Aire :
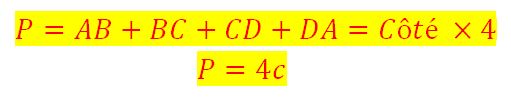
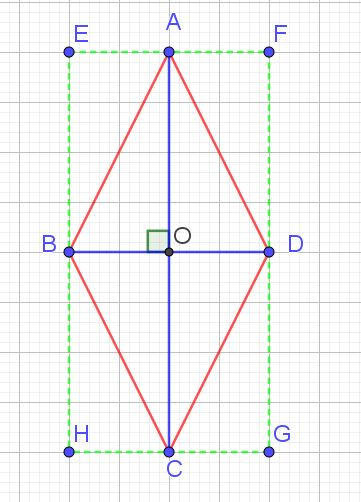
En fait l’aire du losange ABCD est égale à la moitié de l’aire du rectangle EFGH
Le carré
Définition
Un carré est un parallélogramme qui est à la fois rectangle et losange.
Propriétés :
Il a les propriétés
du parallélogramme
du rectangle
du losange
Périmètre et Aire
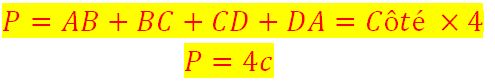
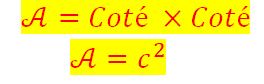
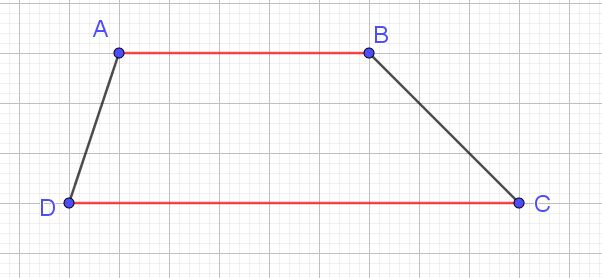
Le trapèze
Définition
Un trapèze est un quadrilatère qui possède deux côtés parallèles.
AB ΙΙ DC
Propriétés
Il peut être isocèle.
AD=BC
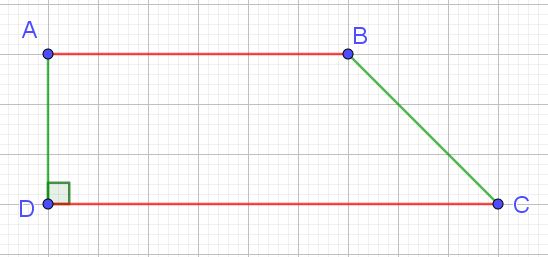
Il peut être rectangle.
ADC = 90°
Périmètre et Aire
