Le triangle
Définition
On attribue à chacun des sommets du triangle une lettre majuscule. Ici A,B et C.
On désigne le triangle par ces trois lettres ABC.
Les côtés du triangle sont désignés par les segments unissant deux sommets : [AB], [AC], [BC], souvent on n’écrit pas les crochets : AB, AC, BC.
On peut nommer aussi chacun des côtés du triangle par le nom de l’angle qui lui est opposé, mais en lettre minuscule a, b, c.
Il existe trois manières de nommer un angle du triangle :
par la seule lettre désignant son sommet;
par trois lettres, celle nommant le sommet de l’angle étant placée au milieu des deux autres;
par une lettre grecque alpha, béta ,gamma.
Triangles particuliers
Triangle isocèle.
Triangle équilatéral.
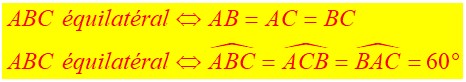
Triangle rectangle.
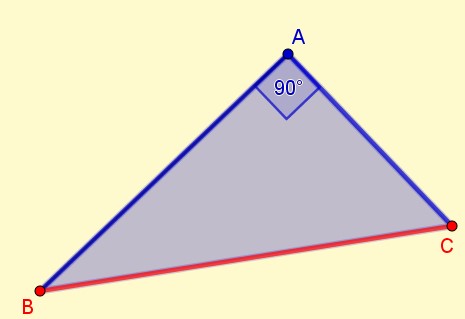
Triangle rectangle isocèle.
Inégalité triangulaire
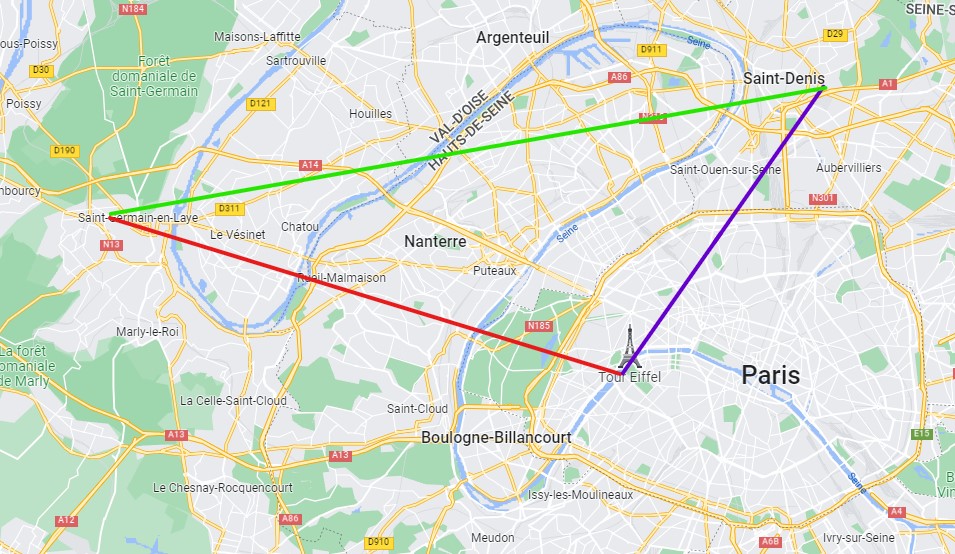
Paris, Saint germain < Paris, Saint-Denis, Saint Germain.
Saint-Germain, Saint-Denis < Saint-Germain, Paris, Saint-Denis.
Saint-Denis, Paris < Saint-Denis, Saint-Germain, Paris.
La ligne droite est le plus court chemin d’un point à un autre.
Un oiseau partant de Paris veut se rendre à Saint Germain en Laye .
Le plus court chemin sera Paris Saint Germain.
Le plus long chemin sera Paris, Saint-Denis, Saint-Germain.
Un fois à Saint Germain il veut se rendre à Saint Denis.
Chemin le plus court : Saint-Germain, Saint-Denis.
Chemin le plus long : Saint Germain, Paris, Saint-Denis.
Une fois à Saint-Denis, il veut revenir à Paris.
Chemin le plus court : Saint-Denis, Paris.
Chemin le plus long : Saint-Denis, Saint-Germain, Paris.
En glissant le curseur vers la droite apparaissent successivement les trois inégalités triangulaires.
Ces inégalités proviennent directement de la définition de la ligne droite qui est le plus court chemin d’un point à un autre.
Dans le premier membre de chaque inégalité on a le chemin entre deux point selon une ligne droite.
Dans le second membre on a le chemin d’un point à un autre selon une ligne brisée.
On ne peut construire un triangle connaissant la longueur de ses côtés que si les inégalités triangulaires sont satisfaites. (Une seule suffit).
Somme des angles d'un triangle
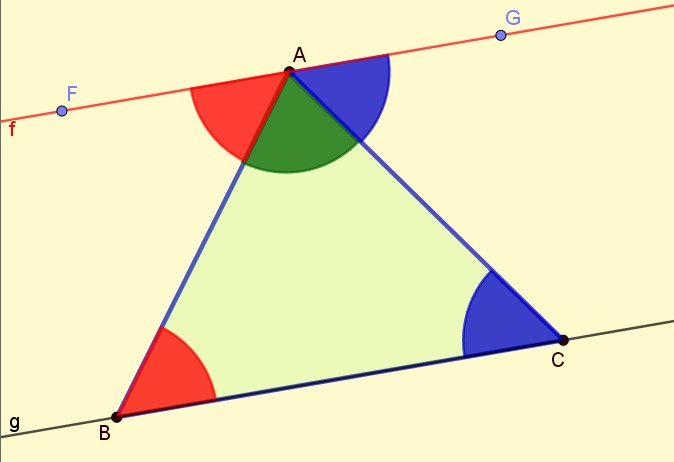
Démonstration :
Soit un triangle ABC.
(g) est la droite passant par B et C .
(f) est la droite parallèle à la droite (g) passant par le sommet A.
Les droites parallèles (f) et (g) sont coupées par la sécante AB.
sont deux angles alternes internes.
Lorsque deux droites sont parallèles coupées par une sécante, les angles alternes internes sont égaux.
(angles rouges)
De même les deux droites parallèles (f) et(g) sont coupées par la sécantes AC.
sont aussi deux angles alternes internes. Donc
La somme des angles 
est égale à l’angle 
qui est un angle plat (180°) puisque les points F, A et G sont alignés appartenant à la même droite (g).
En remplaçant les angles 
par leur angle égal :
La somme des angles du triangle est bien égale à 180°.
Droites remarquables dans le triangle
Droite des milieux
Les médiatrices d'un triangle
Les médiatrices d’un triangle sont les perpendiculaires élevées au milieu de chacun de ses côtés.
Tout point pris sur la médiatrice d’un segment est équidistant des extrémités de ce segment. Et réciproquement tout point équidistant des extrémités d’un segment est sur la médiatrice de ce segment.
Les médiatrices de AB et BC se coupent en O. Donc OA=OB et OB=OC. Par transitivité on déduit de ces deux égalités que OA=OC. Le point O est équidistant de A et de C. Il est situé sur la médiatrice de AC.
Puisque OA=OB=OC. O est équidistant de trois points. Ces points sont situés sur un cercle de centre O. Ce cercle est circonscrit (écrit autour) au triangle ABC.
Les hauteurs d'un triangle
Les hauteurs d’un triangle sont les perpendiculaires menées de chacun des sommets à chacun des côtés opposés.
Les trois hauteurs d’un triangle sont concourantes en un seul point H appelé orthocentre ( ortho=droit).
Voir le démonstration ci dessous.
Les hauteurs d'un triangle : démonstration
Les Médianes d'un triangle
Les médianes d’un triangle sont les droites qui joignent chacun des sommets au milieu du côté opposé.
Il y a donc trois médianes dans un triangle qui se coupent en un seul point G appelé centre de gravité.
Ce centre de gravité est le point où se concentre toute la masse du triangle.
Si on découpe un triangle dans un carton rigide sur lequel on trace son centre de gravité, si on place ce triangle sur une pointe de compas à l’endroit de son centre de gravité, le triangle reste en équilibre, il ne tombe pas.
Les Médianes d'un triangle : démonstration
Les bissectrices d'un triangle
Démonstration :
O’ appartient à la bissectrice de l’angle 
donc il est équidistant des côté de l’angle. O’E=O’F
O’ appartient à la bissectrice de l’angle 
. Il est équidistant des côtés de l’angle. O’E=O’G.
Par transitivité nous avons :
O’E=O’F=O’G et particulièrement
O’F=O’G. O’ est équidistant des côtés de l’angle 
. O’ est donc sur la bissectrice de cet angle.
Les trois bissectrice sont concourantes en O’. Puisque O’E=O’F=O’G= r . O’ est le centre d’un cercle de rayon r inscrit dans le triangle.
Les bissectrices d’un triangle, sont les droites qui partagent chacun des angles du triangle en deux angles égaux.
Puisque le triangle possède trois angle, il aura trois bissectrices qui sont concourantes en un seul point, le centre du cercle inscrit.
Les bissectrices extérieures d'un triangle
Faire glisser le curseur de 0 à 8 en regardant chaque étape.
Un triangle possède trois angles situés à l’intérieur du triangle. Dans la figure ci-contre les 3 angles sont de sommet A,B et C.
SI on prolonge les côtés du triangle , on obtient 9 autres angles situés à l’extérieur du triangle. Trois de ces angles sont opposés par leur sommet avec les angles intérieurs. Nous ne considèrerons que les 6 autres angles. Chacun de ces 6 angles possède une bissectrice.
Les bissectrices extérieures d'un triangle : propriétés.
Pour démontrer que deux bissectrices extérieures et une bissectrice intérieure au triangle sont concourantes au centre d’un cercle exinscrit on utilise la même méthode que celle utilisée pour démontrer que les trois bissectrices intérieures sont concourantes en un point O centre du cercle inscrit
Mettre le curseur à 0 s’il n’y est pas.
Faire glisser le curseur de O à 8 en s’arrêtant à chaque étape.
Droite d'Euler
Jusqu’à présent nous avons utilisé des notions mathématiques apprises au collège en 6ième et 5ième . Pour démontrer l’alignement des trois points en questions nous avons besoin de notions apprises plus tard et notamment la notion de vecteurs.
Donc, nous allons démontrer à nouveau que les médianes sont concourantes et que les hauteurs sont concourantes en utilisant la méthode vectorielle.