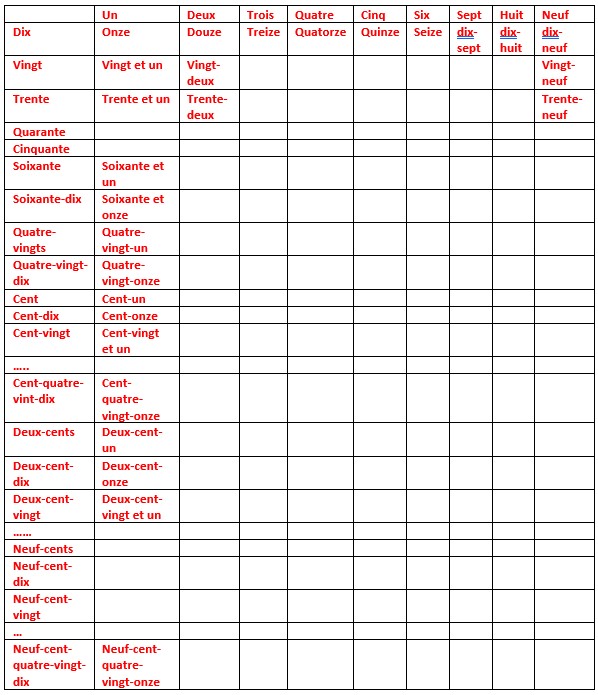
la numération en base 10 CP-6
Compter avec mes doigts
Tout ces bonbons !
Je ne sais pas combien j’en ai.
Je ne sais pas compter.
Comment faire ?
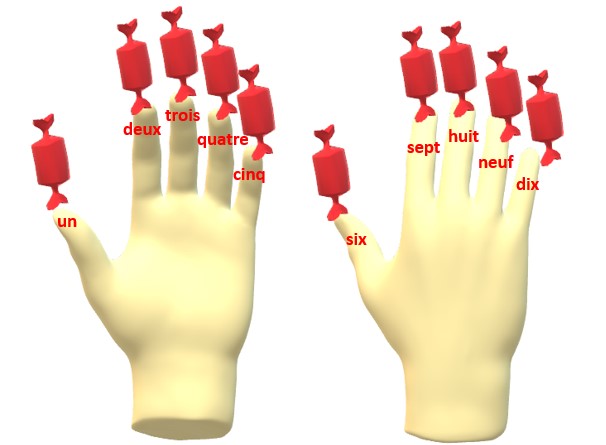
Je sais car on me l’a dit que j’avais dix doigts.
Je vais donc compter avec mes doigts.
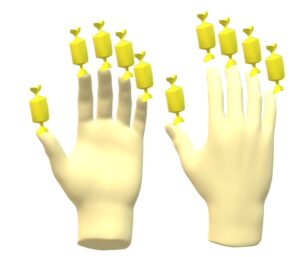
Le pouce de ma main gauche c’est un.
L’indexe de ma main gauche c’est deux.
Le majeur de ma main gauche c’est trois.
L’annulaire de ma main gauche c’est quatre.
L’auriculaire de ma main gauche c’est cinq.
Je continue avec ma main droite.
Le pouce de ma main droite c’est six
L’indexe de ma main droite c’est sept.
Le majeure de ma main droite c’est huit.
L’annulaire de ma main droite c’est neuf.
L’auriculaire de ma main droite c’est dix.
SI je mets un bonbon en face de chacun de mes doigts, je saurais combien j’ai de bonbons.
Mais je n’ai pas assez de doigts !
Je mets en face de chacun de mes doigts les bonbons rouges.
Je vais faire pareil avec les bonbons bleus, les verts, les jaunes et les rouges et blancs.
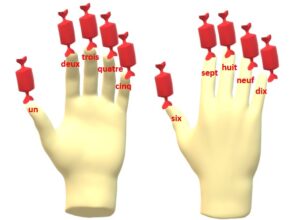
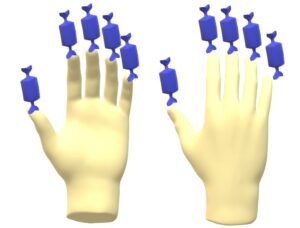
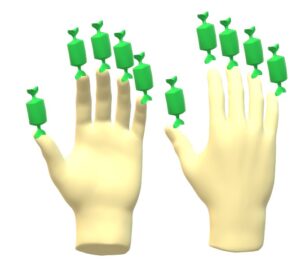
Je sais maintenant que j’ai au moins
dix bonbons rouges
dix bonbons bleus
dix bonbons verts
dix bonbons jaunes
dix bonbons rouges et blancs.
J’ai trouvé, je vais faire des paquets de dix bonbons.
J’appelle un paquet de dix bonbons une dizaine.
J’ai un paquet de dix bonbons rouges et il m’en reste un.
J’ai un paquet de dix bonbons bleus et il m’en reste deux.
J’ai un paquet de dix bonbons jaunes et il m’en reste trois.
J’ai un paquet de dix bonbons verts et il m’en reste quatre.
J’ai un paquet de dix bonbons rouge et blancs et il m’en reste cinq.
Pour les rouges j’ai un bonbon plus une dizaine : un + dizaine =onze
Pour les bleus j’ai deux bonbons plus une dizaine : deux + dizaine=douze.
Pour les jaunes j’ai trois bonbons plus une dizaine. trois + dizaine=treize
Pour les verts j’ai quatre bonbons plus une dizaine quatre + dizaine= quatorze
Pour les rouges et blancs j’ai cinq bonbons plus une dizaine cinq (quinte en latin) + une dizaine =quinze
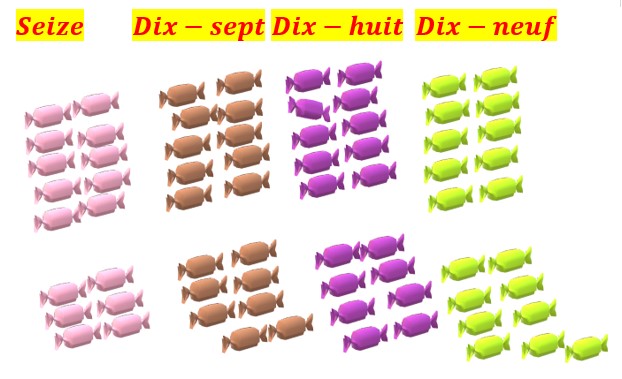
On peut continuer:
Ainsi j’ai six bonbons roses plus une dizaine : six +une dizaine = seize
Mais à partir de là on change de taque tique ( A cause des Romains) et on va inverser et dire :
J’ai une dizaine de bonbons marrons plus sept : dix + sept = dix–sept
J’ai une dizaine de bonbons violents plus huit : dix + huit = dix–huit
J’ai une dizaine de bonbons citrons plus neuf : dix + neuf = dix–neuf
Voyons maintenant comment nommer les paquets de dix
Un paquet de dix c’est une dizaine.
Deux paquets de dix
(rouges +bleus)
viginta en latin qui veut dire deux dix et qui est devenu vingt
Trois paquets de dix
(rouges+bleus+jaunes)
tri ginta trente.
Quatre paquets de dix
(rouges + bleus + jaunes + verts)
quadra gintaquarante.
Cinq paquets de dix
(rouges+bleus+jaunes+verts+rouges et blancs)
Quinqua (cinquanta) ginta : cinquante
Six paquets de dix
(rouges+bleus+jaunes+verts+bicolores+roses)
sexa ginta
Sept paquets de dix (rouges+bleus+jaunes+verts+bicolores+roses+marrons) sept ginta : septante. On garde ce nom en Belgique et en Suisse, en France on préfère dire soixante plus dix : soixante-dix
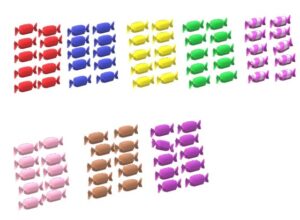
Huit paquets de dix
(rouges +bleus+jaunes+verts+bicolores+roses+marrons+violets)
Octo ginta octante. Mais on préfère dire 4 ,fois vingt : quatre-vingt.
En Suisse on dit soit octante soit huitante.
Neuf paquets de dix
(rouges+bleus+jaunes+verts+bicolores+roses+marrons+violets+citrons)
nonan ginta : nonante. De même on garde nonante en Belgique et en Suisse mais en France on préfère quatre vingt + dix : quatre-vingt dix.
Dix paquets de dix
Si je fais un paquet de ces dix paquets de dix, cela me donne un paquet de dix paquets de dix.
Un paquet de dix paquets de dix c’est un paquet de cent.
Un paquet de dix paquets de dix bonbons : un paquet de cent : cent
Deux paquets de dix paquets de dix bonbons : deux paquets de cent :
deux cents
Trois paquets de dix paquets de dix bonbons : trois paquet de cent :
trois cents
On peut continuer avec quatre, cinq, six sept, huit paquets de dix paquets de dix bonbons :
quatre cents, cinq cents, six cents, sept cents, huit cents.
Enfin neuf paquets de dix paquet de dix bonbons : neuf paquets de cent:
neuf cents.
Dix paquets de cent bonbons se dit mille.
On a ainsi mille bonbons soit dix paquets de dix paquets de dix bonbons
Un paquet de mille
On peut continuer
Deux paquets de mille bonbons : deux mille
trois paquets de mille : trois mille
…
neuf paquets de mille ; neuf mille
Maintenant, tu vas pouvoir compter à l’infini en français
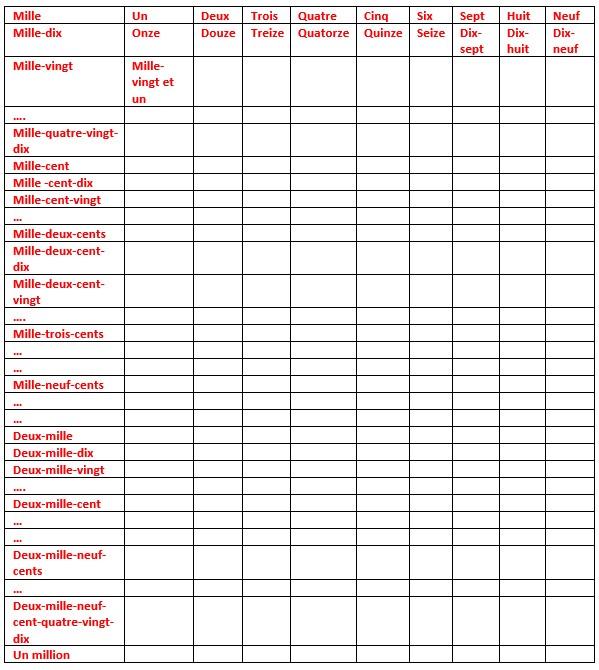
Combien ai-je de bonbons ? 
Deux paquets de mille bonbon
ou deux paquets de dix paquets de cent
ou deux paquets de dix paquets de dix paquets de dix
Quatre paquets de cent bonbons
ou quatre paquets de dix paquets de dix
Six paquets de dix bonbons
Six bonbons seuls
Deux mille
Quatre cents
Soixante
Six
Deux-mille-quatre-cent-soixante-six
Grammaire :
On écrit les nombres avec des tirets entre chaque nombre sauf s’ils sont raccordés par un “et”.
Mille est toujours invariable et s’écrit donc toujours sans “S”.
Cent s’accorde en nombre à condition qu’il n’y ai plus de chiffre après lui.
Compter avec les chiffres
C’est beaucoup plus facile
On dispose de 10 signes.
Zéro correspond à aucun objet, aucun bonbon dans notre cas.
On écrit le nombre d’unité à droite puis sur la gauche les dizaine, les centaines, les milliers …
Mais on lit normalement de gauche à droite.
Ainsi le nombre écrit sur la dernière ligne se lit-il :
Trois millions-six-cent-quarante-deux-mille-cinq-cent-vingt et un
Pour faciliter la lecture du nombre on sépare les chiffres par tranche de 3 à partir de la droite, en introduisant soit un point, soit un espace.
Pour ne pas le confondre avec une virgule, on peut placer le point en haut.
Attention, pour les anlo-saxons la virgule des nombres décimaux que nous aborderons après est représentée par un point.
Les nombres décimaux
Tu sais maintenant compter avec des nombres entiers. Mais comment compter avec un bonbon que l’on partage. Voyons cela avec un gâteau qui est plus simple à partager qu’un bonbon.
.
Ci-contre, une belle bûche de noël.
Je remarque qu’on peut découper dix parts dans cette bûche.
Ainsi dix personnes pourront manger chacune une part de la bûche.
Quand on partage quelque chose en dix, chaque morceau correspond à un dixième.
Ainsi dans une bûche j’obtient dix dixièmes de bûche.
On peut partager une unité en dix parts égales appelés dixième.
Dans une unité, on a dix dixièmes.
Ma maman me donne une part de la bûche partagée en dix.
J’ai donc un dixième de la bûche.
Soit zéro bûche entière mais un dixième. En chiffre cela s’écrit : zéro unité virgule un.
On peut dire aussi que j’ai une part sur dix. En chiffre cela s’écrit un au dessus de dix.
Ma maman sait que je suis gourmand et elle me donne deux parts de la bûche partagée en dix parts.
J’ai donc deux dixièmes de la bûche.
Soit zéro bûche et deux dixièmes. Ce qui s’écrit en chiffre : zéro unité virgule deux.
On peut aussi dire que j’ai deux parts sur dix. Ce qui s’écrit en chiffre deux au dessus de dix.
Ma maman sait que je suis très gourmand et elle me donne trois parts de la bûche partagée en dix parts.
J’ai donc trois dixièmes de la bûche. 
Soit zéro bûche et trois dixièmes. Ce qui s’écrit en chiffre : zéro unité virgule trois.
On peut aussi dire que j’ai trois parts sur dix. Ce qui s’écrit en chiffre trois au dessus de dix.
Ma maman sait que je suis un goinfre et elle me passe tous mes caprices. Tant pis si je suis malade. Elle me donne quatre parts de la bûche partagée en dix parts.
J’ai donc quatre dixièmes de la bûche. 
Soit zéro bûche et quatre dixièmes. Ce qui s’écrit en chiffre : zéro unité virgule quatre.
On peut aussi dire que j’ai quatre parts sur dix. Ce qui s’écrit en chiffre quatre au dessus de dix.
On peut noter que cette part correspond à la moitié de la bûche.
Dix parts de la bûche corespondent à la bûche entière, à une bûche.
Cela correspond à une bûche entière plus une part d’une dixième bûche.
Cela correspond à une bûche entière et à six parts d’une dixième bûche.
Soit deux bûches.
Soit quatre bûches entières et huit parts d’une cinquième.
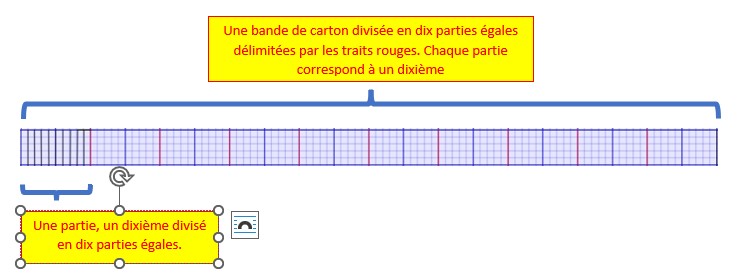
J’ai pris une bande de carton. Avec les traits rouges, je l’ai divisée en dix parties égales. Chaque partie obtenue est appelée dixième.
Ensuite, je divise chaque dixième en dix parties égales. Il y a dix traits bleus entre les traits rouges.
Je compte cent nouvelles divisions dans toute la bande de carton. Ce sont des centièmes.
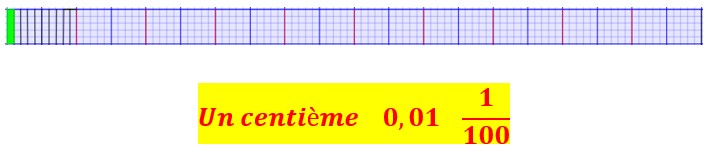
La partie colorée en vert correspond à un dixième de un dixième de la bande, c’est-à-dire à un centième de la bande.
Cela s’écrit en chiffre zéro virgule zéro un
On peut dire aussi une partie sur cent partie, et on va écrire un au dessus de cent.
Pour un dixième en chiffre, on a un chiffre après la virgule car dix s’écrit avec un seul zéro.
Pour un centième en chiffre, on a deux chiffres après la virgule car cent s’écrit avec deux zéros.
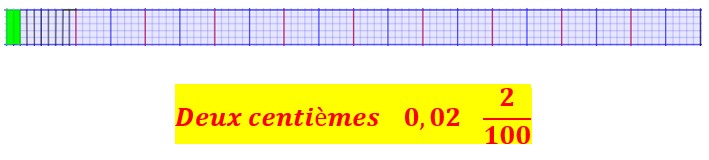
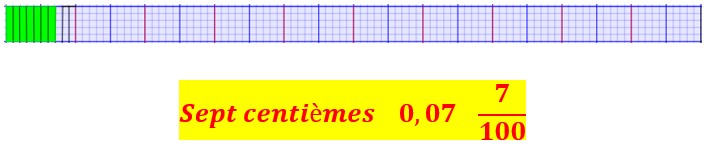
Je vois que dix centièmes de la bande correspondent à un dixième de cette bande.
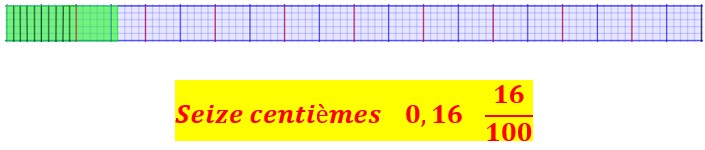
Je vois que seize centièmes de la bande correspondent à un dixième et six centième de cette bande.
Je vois que trente-cinq centièmes de la bande correspondent à trois dixième et cinq centième de cette bande.
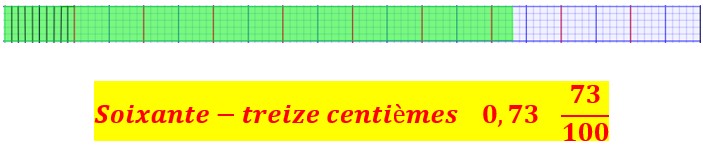
Je vois que soixante-treize centièmes de la bande correspondent à sept dixièmes et trois centièmes de cette bande.
Je vois que cent centièmes de la bande correspondent à dix dixièmes de cette bande et finalement à la bande entière.
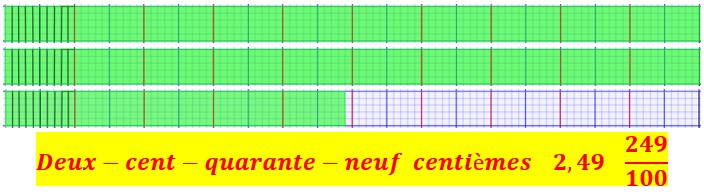
Je vois que deux-cent-quarante-neuf centièmes de bandes correspondent à vingt-quatre dixièmes et neuf centièmes de bandes et aussi à deux bandes et quatre dixième et neuf centièmes de bandes.
On peut continuer à partager :
En partageant une unité en dix j’obtiens des dixièmes d’unité.
En partageant un dixième d’unité en dix j’obtiens des centièmes d’unité.
En partageant un centième d’unité en dix j’obtiens des millièmes d’unité.
En partageant un millième d’unité en dix j’obtiens des dix-millièmes d’unité.
En partageant un dix-millième d’unité en dix j’obtiens des cent-millièmes d’unité.
En partageant un cent-millième d’unité en dix j’obtiens des millionièmes d’unité.
On peut continuer indéfiniment.
De même lorsque j’ai dix unités j’obtiens une dizaine d’unités.
Lorsque j’ai une dix dizaines d’unités j’obtiens une centaine d’unités.
Lorsque j’ai dix centaines d’unité j’obtiens un millier d’unités.
Lorsque j’ai dix milliers d’unités j’obtiens un dix-millier d’unité.
Lorsque j’ai dix dix-milliers d’unités j’obtiens des cent-milliers d’unités.
Lorsque j’ai dix cent-milliers d’unités j’obtiens un milliard d’unités.
Tout cela est résumé dans le tableau ci-dessous.
Récapitulatif
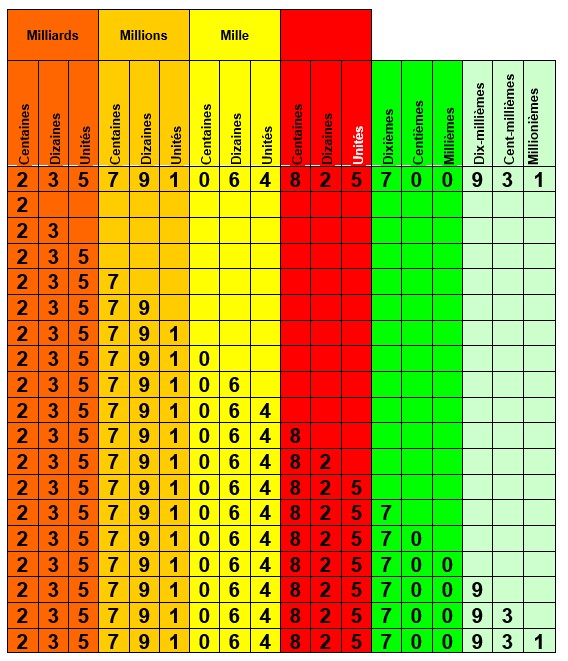
Ne pas confondre le chiffre des dizaines par exemple avec le nombre de dizaines.
Le nombre de la première ligne du tableau ci-contre se lit :
deux cent trente cinq milliards sept cent quatre vingt onze millions soixante quatre mille huit cent vingt cinq et sept cent mille neuf cent trente et un millionième.
En chiffre, il s’écrit :
235 791 064 825,700 931
235.791.064.825,700.931
C’est un nombre décimal.
Il s’écrit avec une virgule après les unités.
Pour mieux le lire on regroupe les chiffres par trois et on sépare chaque groupe par un espace ou un point.
Le chiffre des centaine de milliards de ce nombre est 2
Il a 2 centaines de milliards .
Le chiffre des dizaines de millions est 9
Il a 23 579 dizaines de millions.
Le chiffre des dizaines est 2.
Il a 23 579 106 482 dizaines
Le chiffre des dix-millième est 9.
Il a 2 357 910 648 257 009 dix millièmes