Mouvement d’une balle de tennis dans un champ de pesanteur
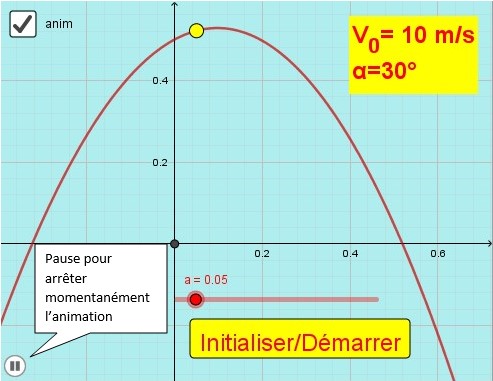
premier clic : initialise l’animation, met le curseur à zéro
Deuxième clic :démarre l’animation
un logo “pause” apparaît en bas à gauche de l’animation.
un clic pour arrêter momentanément l’animation.
un clic pour reprendre l’animation
On peut aussi déplacer la balle en pointant soit le curseur, soit la balle avec la souris.
Objet d'étude, la balle de tennis.
Nous allons étudier le comportement d’une balle de tennis lorsqu’elle est lancée par le joueur.
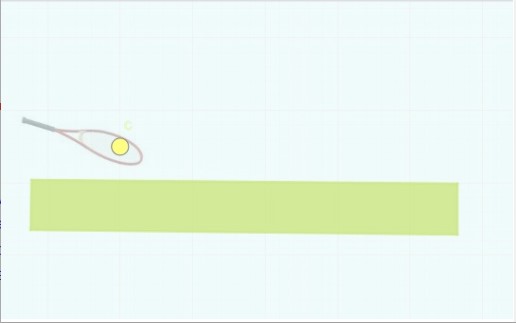
La balle est sur la raquette et le joueur lui donne une impulsion, lui administre une certaine vitesse qui va permettre à la balle de se déplacer en l’air jusqu’à ce qu’elle retombe sur le sol. le joueur tient sa raquette selon un certain angle.
Nous voyons à l’œil nu qu’elle se déplace approximativement selon un arc de cercle. Elle monte, puis elle redescend jusqu’au sol.
Si le joueur change l’angle de sa raquette et/ou la force de son impulsion, c’est-à-dire la vitesse de la balle au départ, la trajectoire de cette balle est totalement changée.
Elle semble toujours décrire un arc de cercle. Mais elle monte moins haut et va un peu plus loin.
Tout l’art du joueur de tennis semble donc résidé dans la manière de tenir sa raquette selon un certain angle et l’impulsion, c’est-à-dire la vitesse, qu’il donne à la balle.
Début du problème
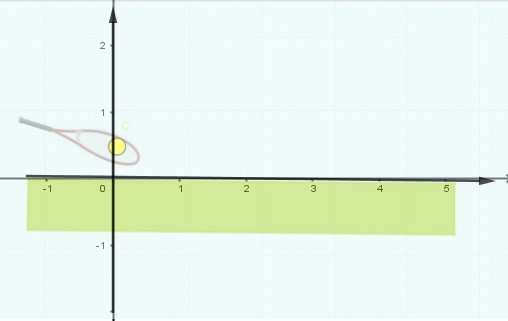
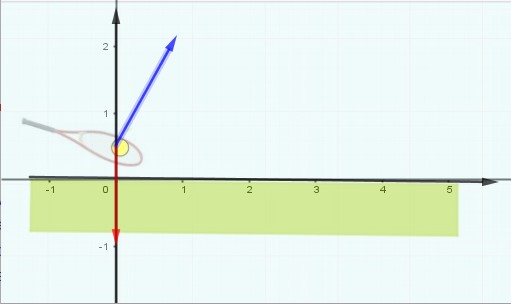
Pour traiter mathématiquement ce problème, nous avons besoins de connaître à tout moment t la position de la balle, savoir à tout moment t où elle se trouve. Pour cela nous allons créer un repère.
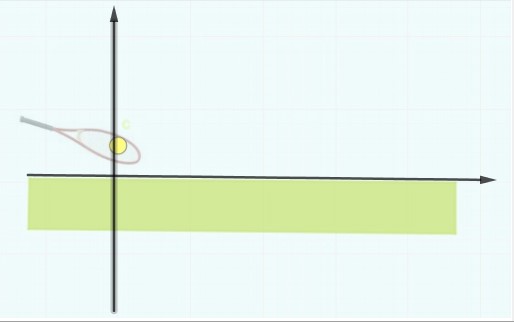
D’abord un axe horizontal orienté de gauche à droite qui sera situé au niveau du sol. Les pieds du joueur sont situés sur cet axe. (D2).
Puis un axe vertical passant par le centre de gravité de la balle au moment où elle va être lancée orienté de bas en haut. (D3)
Il faut graduer ces deux axes pour positionner la balle à tout moment avec deux nombres (sa position horizontale ou abscisse, sa position verticale ou ordonnée) (D4). Comme unité sur les axes on peut choisir le mètre.
La balle est soumise à son poids, résultat de l’attraction terrestre figuré par un vecteur rouge vertical de haut en bas. (D5)
Elle est soumise au moment du lancer uniquement à l’impulsion du joueur qui lui transmet ainsi une vitesse représentée par un vecteur bleu perpendiculaire à la raquette. On suppose que le joueur ne donne aucun effet à sa balle. (D6). La force d’impulsion ne dure qu’un très court moment et disparaît ensuite.
Mathématisation du problème
Vecteur accélération
Normalement le joueur de tennis lance la balle dans l’espace. Et nous devrions avoir un repère en trois dimension, Ox, Oy, Oz pour étudier le déplacement de la balle. Mais intuitivement et on peut le démontrer, la balle reste toujours dans la même plan sauf si à un moment donné un coup de vent la fait dévier de sa trajectoire.
Aussi étudierons nous ce problème en deux dimension avec un repère dans le plan Ox, Oy .
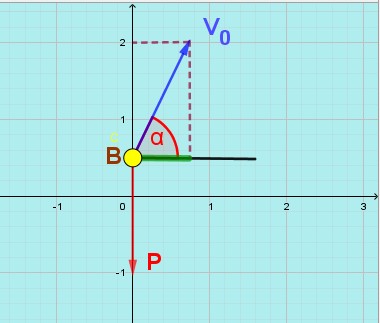
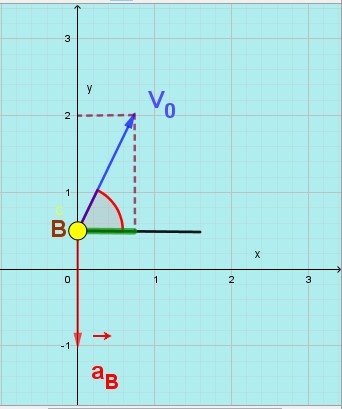
Au temps t=0, c’est-à-dire au moment où elle quitte la raquette après que le joueur l’a frappée, la balle n’est soumise qu’à une seule force, son poids qui l’attire vers le sol (vers le centre de la terre).
La somme des forces extérieures exercée sur la balle est donc uniquement son poids P.
Cette force est constante.
D’après la seconde loi de newton :
Un solide soumis à une force constante est animé d’un mouvement uniformément accéléré d’accélération
Donc 
Nous savons aussi que le poids d’un corps est égal au produit de sa masse par le vecteur accélération 
de la gravité terrestre.
Nous en déduisons 
Désignons l’accélération de la balle par 
Les composantes ou coordonnées de ce vecteur vertical de haut en bas sont donc :
Et en fonction du temps t, ce vecteur reste constant.
Nous avons donc pour décrire le système deux phénomènes :
Une accélération représentée par un vecteur aB vertical de haut en bas et égal à l’accélération g de la pesanteur terrestre.
Une vitesse initiale représentée par un vecteur V0 faisant un angle α avec l’horizontale et de valeur V0
Vecteur vitesse instantanée.
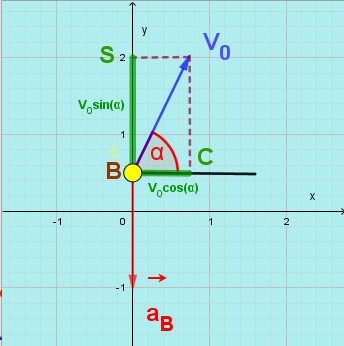
A l’état initial la balle est animée d’une vitesse V0 représentée par un vecteur dont les coordonnées sont (d’après le théorème de Pythagore) :
Le vecteur accélération, nous l’avons vu précédemment, possède deux composantes (deux coordonnées). Il est constant, il ne varie pas avec le temps car la valeur de g est constante. 
Le vecteur accélération est la dérivée du vecteur vitesse par rapport au temps. On connaît le vecteur accélération, il faut trouver le vecteur vitesse. Il suffit d’intégrer les deux composantes du vecteur accélération. 
Ce vecteur est représenté en bleu sur l’animation ci-contre.
Sa direction et sa norme (sa longueur), autrement dit la valeur de la vitesse de la balle en m.s-1 changent en fonction du temps t.
A l’instant t=0 le joueur lance la balle selon un angle de 45° avec l’horizontale à une vitesse de 2 mètres par seconde.
A partir de ce moment, la balle monte, sa vitesse diminue ainsi que l’angle avec l’horizontale.
A l’instant t=0,14 s la balle a atteint une altitude maximale et l’angle avec l’horizontal est nul.
Puis la balle redescend, sa vitesse augment ainsi que l’angle jusqu’à ce q’ elle atteigne le sol au temps t=0.44
Vecteur position.
Sur l’axe des abscisses, la projection de la balle (son abscisse) se déplace en fonction du temps t
Sur l’axe des ordonnées, la projection de la balle (son ordonnée) se déplace aussi en fonction du temps t.
Les équations de ces fonctions sont données par les coordonnées du vecteur OB ci-dessus. C’est le vecteur vert OB qui indique à chaque instant t la position de la balle B dans le repère.
A l’état initial, au moment du lancé, la balle se situe à 0.50 du sol qui correspond à la hauteur de la raquette par rapport au sol lorsque le joueur frappe la balle.
Les composantes ou coordonnées du vecteur OB sont donc :
Nous savons que le vecteur vitesse est la dérivée du vecteur position 
il suffit d’intégrer les coordonnées du vecteur vitesse pour obtenir les coordonnées du vecteur position 
Les coordonnées du vecteur vitesse ont été calculées précédemment. Intégrons les (nous ne donnerons pas les détails sur ce calcul)
Les constantes 3 et 4 correspondent aux valeurs des conditions initiales du vecteur OB au temps t=0 c’est-à-dire respectivement 0 et 0,5
Dans les deux animations identiques ci-contre (La seconde laisse la trace de la balle), le joueur lance la balle à une vitesse V0 de 10 mètres par seconde avec un angle α de 45°.
Juste après le lancé, la balle monte jusqu’à une certaine altitude puis elle redescend pour toucher le sol.
Nous voyons avec la seconde animation que la balle suit une trajectoire parabolique.
Equations horaires, résumé.
Dans cette animation la vitesse initiale de la balle est de 1mètre par seconde avec un angle de 45°.
Nous résumons ci-dessous les trois équations horaires, équations en fonction du temps t.
Le vecteur accélération a (en rouge) Il est constant :
Le vecteur vitesse en bleu dont l’origine n’est plus le point origine des axes O mais le point B, c’est-à-dire la balle
Le vecteur position OB en vert. La balle représentée par le point B est à l’extrémité du vecteur position. La trace de la balle, ses positions successives est visible en jaune.
Equation cartésienne de la trajectoire.
Dans cette animation le joueur donne une petite impulsion de 10 m/s soit 36 km/h avec un angle de 30° par rapport à l’horizontale (par rapport au sol). Sa raquette se trouve à 0,50 mètre du sol lorsqu’il frappe la balle.
A partir des deux équations horaires du vecteur position, nous pouvons calculer l’équation cartésienne de la trajectoire de la balle de tennis. 
Il suffit de calculer t dans l’une des deux équations. Il est plus facile de choisir la première.
On remplace t par sa valeur dans la seconde équation. 
0,5 est la position de la balle à l’origine, au temps t=0. Cette position peut être symbolisée par y0.
Cette équation est du genre ax²+bx+c. C’est donc une parabole. La balle de tennis décrit une potion de cette parabole.
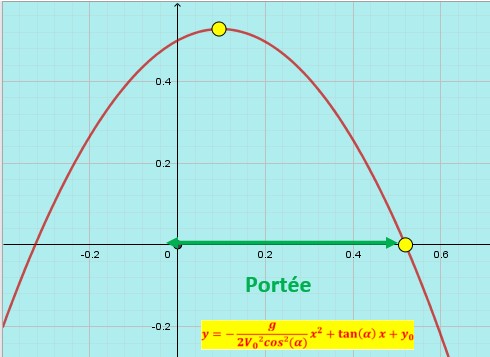
Flèche et portée.
La flèche correspond à l’altitude maximale atteinte par la balle de tennis. C’est l’ordonnée maximale. C’est aussi l’ordonnée du sommet de la parabole.
La portée est la distance de l’origine au point d’impacte de la balle au sol.
Calcul de la flèche
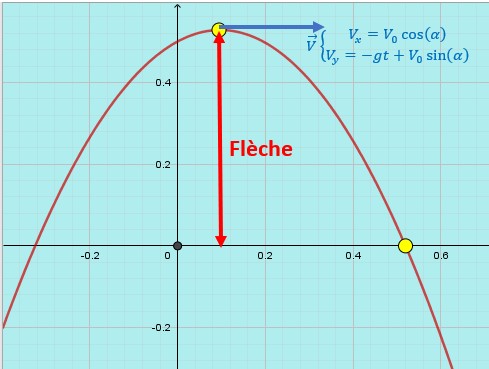
En considérant l’équation horaire du vecteur vitesse :
Lorsque la balle atteint le sommet de la parabole, la composante verticale de sa vitesse est nulle.
On reporte cette valeur dans la composante verticale de l’équation horaire du vecteur position :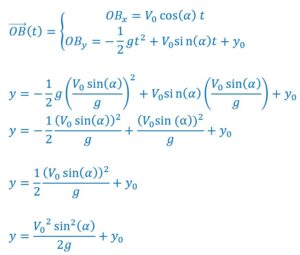 
Autre calcul :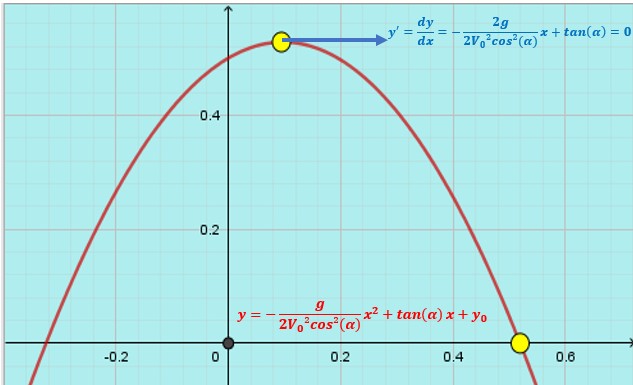
On considère l’équation cartésienne de la trajectoire de la balle.
La balle est au sommet de la parabole. A cet endroit la dérivée de la trajectoire est nulle. (le calcul de la dérivée est évident. 
On calcule :
On trouve l’abscisse pour laquelle la balle est à son apogée.
Il suffit de remplacer cette valeur dans l’équation cartésienne.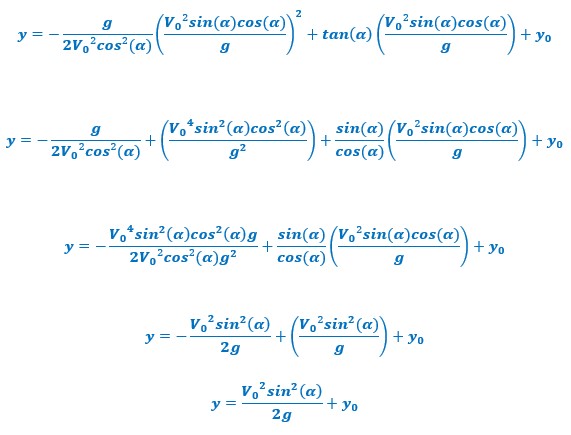 
On trouve, bien sûr le même résultat.
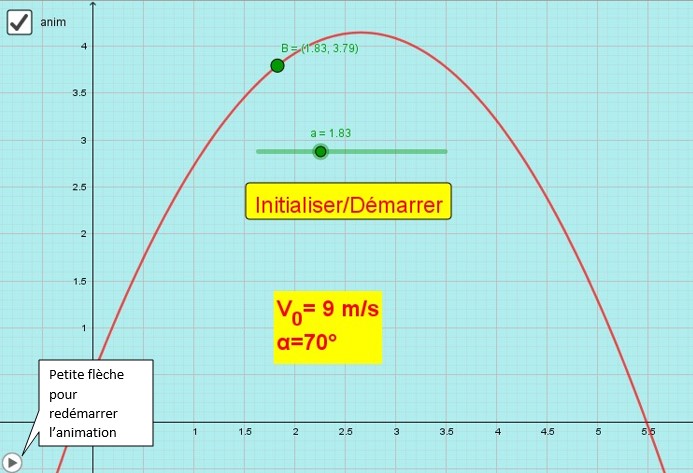
Dans l’animation ci-contre, le joueur lance la balle à une vitesse de 7mètres par seconde avec un angle de 70 degrés.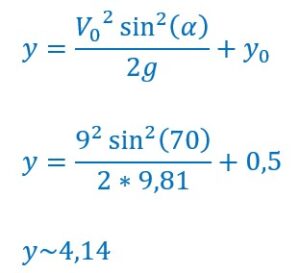 
Les calculs concordent avec l’animation.
Calcul de la portée.
Lorsque la balle est retombée sur le sol, son ordonnée est nulle 
On obtient une équation du second degré qu’il suffit de résoudre. Mais la résolution générale de cette équation aboutit à des calculs très compliqués.
Aussi allons nous calculer la portée lorsque y0=0, c’est-à-dire lorsque la balle part du sol et non plus à 0,5 m du sol
On obtiendra la valeur maximale de la portée pour sin(2α)=1, ce qui correspond à un angle de 90° . 2α=90° d’où α= 45°.
Pour que la balle aille le plus loin possible, elle doit être lancée pour une vitesse donnée selon un angle de 45° avec l’horizontale.
Dans l’animation ci-contre, la balle jaune est frappée depuis l’origine des axes, à terre. Cela facilitera les calculs pour l’expression de la portée. L’équation de la trajectoire de la balle devient :
Lorsque la balle est au sol y=0 d’où :
Et là, on peut factoriser par x :
C’est une équation produit qui possède deux solutions : 
La solution x=o correspond au départ de la balle. Calculons la seconde solution. 
Or d’après les relations trigonométriques, nous savons que 2sin(a)cos(a)=sin(2a)
Dans cette animation, la balle part depuis 0,5 m du sol avec
V0 = 9m/s α = 70° g = 9,81 Y0 = 0,5 m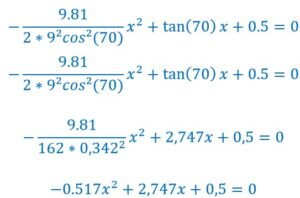
x’ est compatible avec l’animation. Pour x” on devrait trouver 0 mais compte tenu des arrondis et des imprécisions..
Trajectoire de la balle en fonction de l'angle.
Trajectoire de la balle en fonction de la vitesse.
Autres trajectoires
Frappe horizontale.
Le joueur frappe la balle horizontalement à 2,4 mètres du sol, le bras tendu vers le haut. Il lui transmet une vitesse de 7 mètres par secondes.
La trajectoire de la balle est une portion de parabole d’équation :
le joueur frappe la balle lorsqu’elle se trouve à 2,4 m du sol. Son bras est tendu vers le haut. Il lui induit un vecteur vitesse de 7 mètres par seconde ayant un angle de -20° par rapport à l’horizontal. Cet angle est négatif car il est orienté depuis l’horizontale en pointillés jusqu’au vecteur, dans le sens inverse du sens trigonométrique.
La balle suit une portion de trajectoire parabolique dont l’équation générale est :
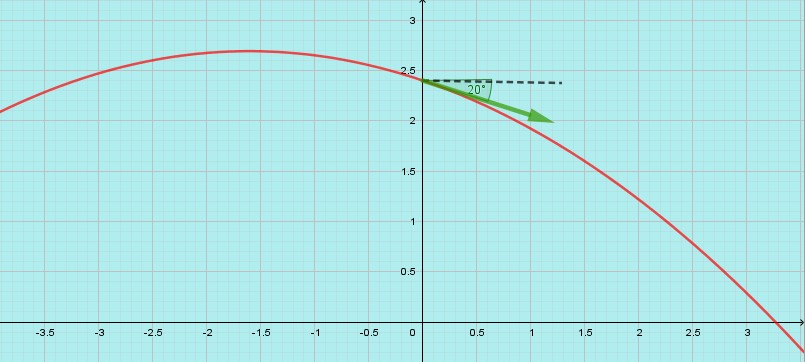
Cette fois le joueur frappe la balle lorsqu’elle se trouve à 2,4 mètre du sol avec un angle de -40 degrés. Il s’agit d’un smash. Il applique à la balle une vitesse de 7 mètres par seconde.
La trajectoire de la balle est une portion de la parabole d’équation générale :
Remarques
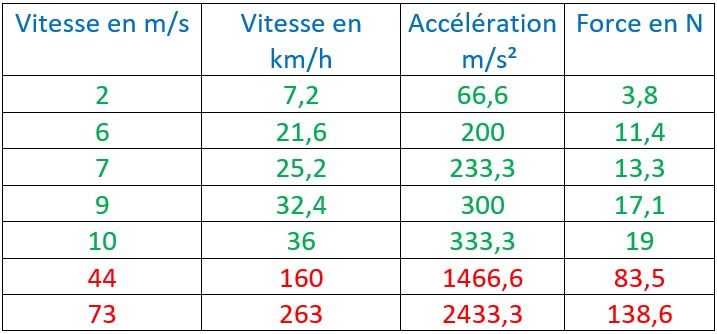
Pour des raisons techniques avec geogebra, nous avons choisi des vitesses de la balle faibles. Elles sont notées en vert dans le tableau ci-contre.
En réalité la vitesse moyenne d’une balle de tennis est d’environ 44 m/s, sachant que le record est de 73 m/s. Elles sont notées en rouge dans le tableau.
Pour connaître la force en Newton (pour la connaître en kilogramme/force, il suffit de la diviser par 10 (9,81 en réalité)
Avant que le jouer ne frappe la balle, celle-ci possède une vitesse nulle. Elle acquiert une vitesse V0 en 3/100 de seconde. La vitesse augmentant de 0 à V0 en 3/100 de seconde l’accélération de la balle sera : a=V0/t=V0 x 100/3.
Sachant qu’une balle a une masse de 57 g la force nécessaire pour inculquer cette accélération sera f=ma=0,057 x V0 x 3/100.
C’est au temps t=0 que la balle possède la vitesse V0.