Système d’équations à deux inconnues
- par gabriel
- dans Equations inéquations, Mathématiques
- sur 1 juin 2019

Parfois dans un problème on demande de trouver deux valeurs distinctes (prix du kg pommes et prix du kg de poires par exemple). Nous avons donc deux inconnues. Pour pouvoir résoudre ce problème, il est absolument nécessaire d’établir deux équations.
Toujours autant d’équations que d’inconnues
On obtient ainsi un système de deux équations à deux inconnues que nous allons apprendre à résoudre de 4 manières différentes.
Combinaison linéaire

Le but est d’éliminer une inconnue pour obtenir une équation à une inconnue. Si j’ai le même nombre de y dans la première équation et que j’additionne membre à membre les deux équations j’aurai atteint mon but.
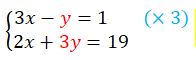
Je multiplie par 3 les deux membre de la première équation.

J’additionne membre à membre les deux équations.

les y s’annulent et il ne reste qu’une équation à une inconnue que je sais résoudre.
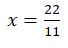
![]()
J’obtiens la valeur de la première inconnue x.

Je reporte cette valeur de x dans l’une des deux équations : par exemple la première.


J’obtiens la valeur de la deuxième inconnue.

![]()
Je reporte les valeurs des deux inconnues dans l’autre équation, la deuxième, pour vérifier. C’est juste.
Autre combinaison linéaire
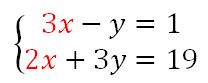
J’ai le même système, mais cette fois je vais éliminer les x. Pour cela je dois m’arranger pour avoir le même nombre de x dans les deux équation.
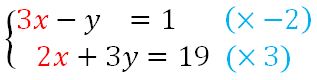
Je multiplie les deux membres de la première équation par -2 et les deux membres de la seconde par 3 pour obtenir 6x dans les deux.
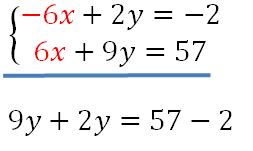
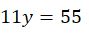
![]()
J’additionne membre à membre les 2 équations.
J’obtiens la valeur de y.
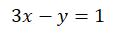
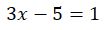
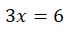
![]()
Je reporte la valeur de y dans la première équation pour obtenir la valeur de x.
Puis pour vérifier je reporte les deux valeurs dans la seconde équation comme au paragraphe ci-dessus.
Substitution

Autre façon :
Je calcule la valeur d’une inconnue en fonction de l’autre inconnue dans une équation. Je reporte cette valeur dans l’autre équation. Prenons toujours le même exemple.
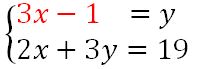
Je calcule y en fonction de x dans la première équation.
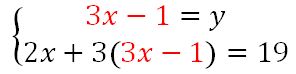
Je reporte cette valeur dans la seconde équation.
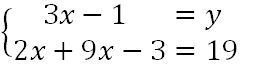
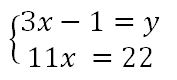
Je développe et réduit la seconde équation.
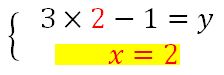
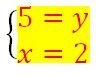
J’obtiens la valeur de x que je reporte dans la première équation.
J’obtiens les deux valeurs de x et y.
Pour vérifier je les reporte dans la seconde équation comme au premier paragraphe.
Déterminant de Cramer

Soit un système de deux équations à deux inconnues de forme générale ci-contre. Les lettres A,B et C repèrent respectivement les coefficients de x, de y et les nombres connus. 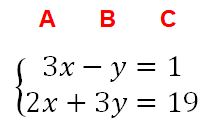
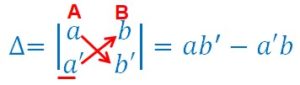
On appelle déterminant du système, le nombre défini ci-contre en prenant les coefficients A et B.
On le note Δ.
S’il est différent de 0, le système a une solution unique x et y.
Si non il n’a pas de solution. 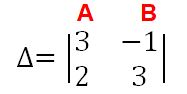
![]()

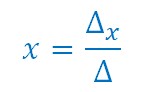
Le déterminant de x est le nombre ci contre Δx calculé à partir des coefficients C et B.
On en déduit la valeur de x.
![]()
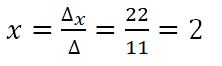

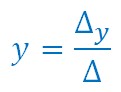
Le déterminant de y est le nombre ci-contre Δy calculé à partir des coefficients A et C.
On en déduit la valeur de y.
![]()

Résolution graphique
Soit le système d’équations :
L’équation (1) est l’équation cartésienne d’une droite f 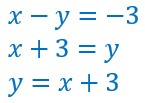
De même l’équation (2) est l’équation cartésienne d’une droite g 
Pour construireune droite il nous faut définir deux points :
pour la droite f :
Pour la droite g 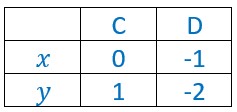
Sur le graphique ci-dessous appuyer successivement sur la double flèche tournée vers la droite pour construire les droites f et g
Problèmes
Ils ont été tirés d’un site dont le lien est ci-dessous.
http://www.col-verne-illzach.ac-strasbourg.fr/disciplines/maths/manuels/3eme/manuel_chapitre_3N4.pdf
Un laboratoire dispose de deux solutions de chlorure de sodium (sel de cuisine) de concentration
20 grammes par Litre pour l’une et 50 grammes par Litre pour l’autre . Quelle volume de chaque solution doit-on mélanger pour obtenir 10 Litres de concentration à 32 grammes par Litre.


Désignons par
x le volume de solution à 20g/L
y le volume de solution à 50 g/L
Au total on doit obtenir 10 L de solution.
On peut donc écrire que le volume de la première solution plus le volume de la seconde solution sera égal à 10 Litres.![]()
Ensuite on va calculer la quantité de chlorure de sodium présent dans chacune des solutions et dans la solution finale.
Si on prélève x Litres de chlorure de sodium à 20 g par Litre, on aura ![]()
Si on prélève y litres de chlorure de sodium à 50 g par Litre, on aura ![]()
Finalement si on doit avoir 10 Litres de solution à 32 g par Litre on aura ![]()
Ainsi on peut écrire :![]()
On obtient un système de deux équations à deux inconnues :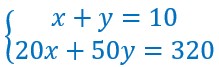
Il suffit de résoudre ce système selon la méthode de ton choix.
Monsieur Seguin possède un terrain triangulaire qu’il veut partager selon le schéma ci-dessous pour enclore sa chèvre qui, éprise de liberté a tendance à s’échappée.
Quelle longueur de fil électrique devra-t-il acheter pour clore le terrain vert en BC et DE ?
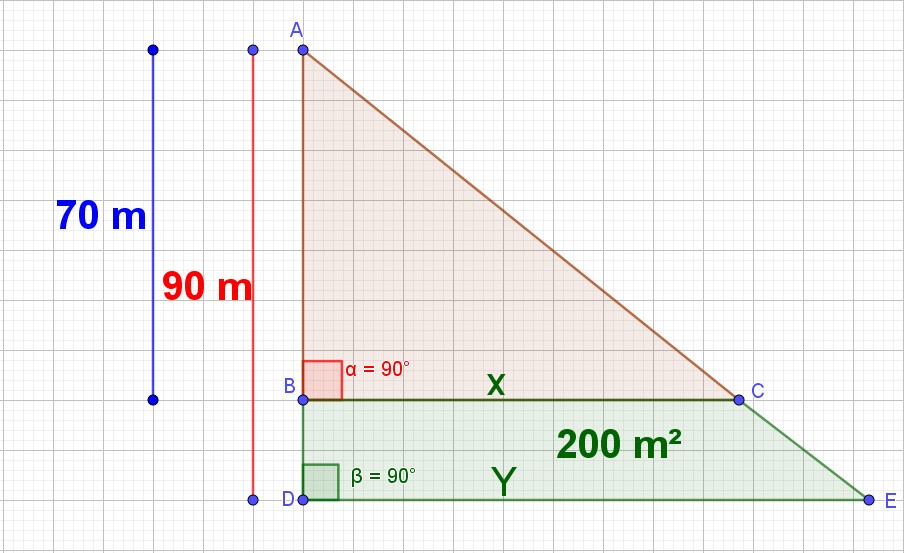

Première chose à voir :
Les segments BC et DE sont tous les deux perpendiculaires à AD, donc ils sont parallèles.
A partir de là, on peut utiliser le théorème de Thalès dans le triangle ABC.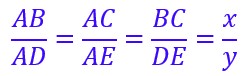
En ne gardant que les égalités qui nous intéressent et en remplaçant les segments par leur valeur on obtient : 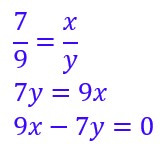
Ainsi on a une première équation.
Le quadrilataire BCED est un trapèze dont l’aire est égale à 200 m².
L’aire d’un trapèze est :
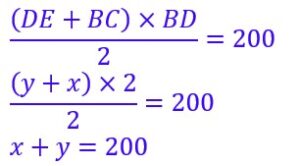
On obtient une seconde équation et donc un système de 2 équations à 2 inconnues. 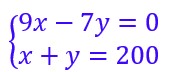
A résoudre.

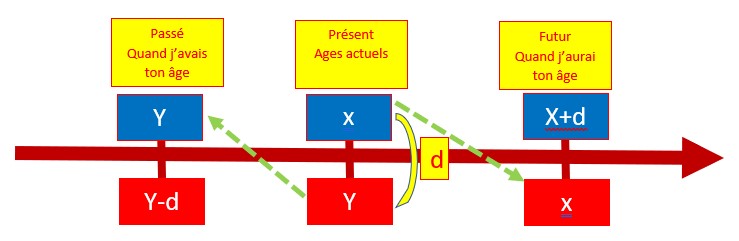
J’ai trois fois l’âge que tu avais quand j’avais l’âge que tu as.
Oh que c’est difficile !
Manifestement l’ainé, le plus âgé est le garçon.
Si je désigne par x l’âge actuel du garçon et par y l’âge actuel de la fille, et si d est la différence des deux âge qui est constante (d=x-y) on peut traduire :
Quand j’avais ton âge y toi tu avais y-d et j’ai actuellement trois fois ton âge de l’époque soit 3(y-d); Or mon âge actuel est x.
Donc x=3(y-d)![]()
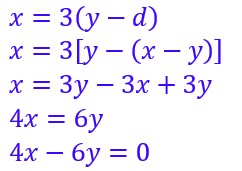
Quand j’aurai ton âge, on aura 42 ans à nous deux.
Quand j’aurai ton âge actuel c’est à dire x, toi tu aura x+d
x+x+d=42
On obtient un système de deux équations à deux inconnues qu’on résout comme on veut. 