Second degré
Sommaire
Introduction
Une expression algébrique du premier degré s’écrit :ax+b.
ce peut être une fonction : f(x)=ax+b a et b étant des nombres appartenant aux nombres réels
ce peut être une équation ax+b=0 par exemple.
On dit que cette expression est du premier degré parce que la variable dans le cas d’une fonction ou l’inconnue dans le cas d’une équation est du premier degré 😡 puissance 1 ou x exposant 1 ou x tout simplement.
Une expression algébrique du second degré s’écrit ax²+bx+c a,b,c étant aussi des nombres réels
Une fonction du second degré sera du type f(x) = ax²+bx+c
Une équation du second degré sera du type ax²+bx+c=0
Fonction du second degré
Construction de la courbe représentative
Une fonction du second degré est de la forme 
sachant que a; b ou c peuvent prendre n’importe quelle valeur dans l’ensemble des nombres réels.
Prenons un exemple avec la fonction suivante 
a=2 ; b=-2 et c=-4
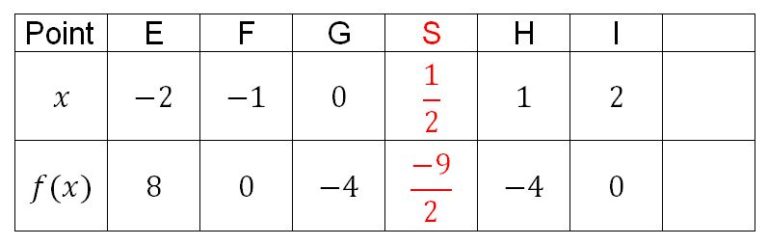
A partir de cette formule, on peut établir un tableau de valeurs ci-contre en calculant successivement d’après la formule donnée f(-2); f(-1);….
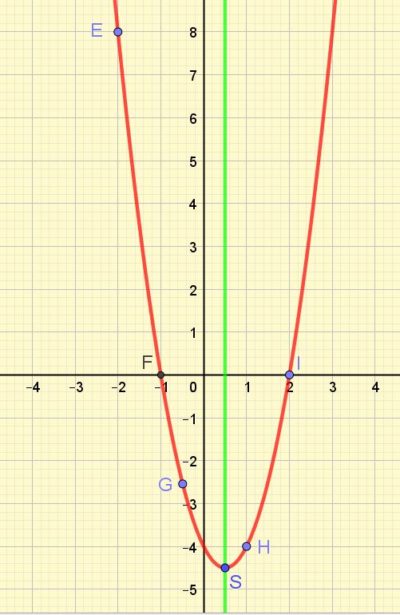
Et à partir de ce tableau de valeurs, il suffit de placer les points E;F;G… sur un graphique et les joindre pour avoir la représentation graphique de cette fonction qui est une parabole.
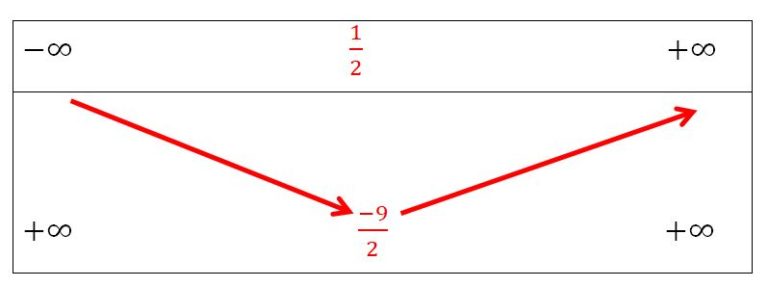
D’après ce graphique, on peut établir son tableau de variation.
Elle est décroissante de moins l’infini jusqu’au point S d’abscisse un demi ]-∞;1/2] ; puis elle est croissante du point S à plus l’infini [1/2;+∞[.Le point
est appelé extremum, dans ce cas c’est un minimum.
La droite verte d’équation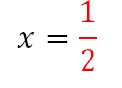 
est un axe de symétrie de la parabole.
Forme canonique
Nous allons trouver une autre manière d’écrire la formule de départ qui nous permettra de trouver les coordonnées de l’extremum. Cette autre manière est appelée forme canonique.
Accrochez-vous, il faut bien se concentrer pour les calculs.
On factorise par a
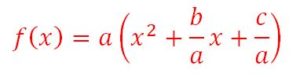
est le début d’une identité remarquable :
Le double produit de cette identité remarquable est : 
Il nous faut trouver le carré du deuxième nombre. 
Notre identité remarquable est donc :
Reprenons notre fonction là où on en était rester. Pour faire apparaître notre identité sous forme développée, on lui ajoute le carré de ce deuxième nombre. Mais pour ne pas changer la fonction, si on lui ajoute quelque chose il faut immédiatement le soustraire. Et notre fonction devient :
On peut écrire la fonction comme ci-dessous pour bien faire apparaître l’identité remarquable sous forme développée. 
ou encore sous forme factorisée :
On distribue a puis on simplifie :
On réduit les deux derniers termes au même dénominateur 4a :
On peut écrire encore, en mettant les deux derniers termes sur la même barre de fraction (attention au signe négatif devant la barre).
Voyons maintenant un cas particulier de la variable x :
alors
On obtient ainsi deux valeurs particulières qui sont l’abscisse et l’ordonnée d’un point S de la parabole appelé extremum (maximum ou minimum). On peut dire approximativement que cet extremum est le “sommet” de la parabole.
On désigne par α l’abscisse de cet extremum et par β son ordonnée.
Notre expression
peut s’écrire :
C’est la forme canonique de notre fonction.
On connaît maintenant les coordonnées du sommet S :
et l’équation de l’axe de symétrie de la parabole :
On factorise par 2.
est le début d’une identité remarquable.
Le double produit de cette identité est 
Il faut trouver le deuxième terme :
L’identité remarquable est donc :
Reprenons notre fonction là où on en était rester et pour faire apparaître notre identité sous forme développée, on lui ajoute le carré de ce deuxième nombre. Mais pour ne pas changer la fonction, si on lui ajoute quelque chose il faut immédiatement le soustraire. Et notre fonction devient :
Qu’on peut écrire en faisant apparaître en rouge l’identité remarquable sous forme développée :
autre écriture sous forme factorisée:
On aboutit finalement à :
On distribue le terme 2 :
Et finalement :
On obtient la forme canonique de la fonction décrite ci-contre à gauche avec 
On calcule généralement α et β à partir de l’expression originelle
Et ainsi on obtient l’extremum S de la parabole :
revenons à la forme canonique :
Mettons 2 en facteur :
En remarquant que :
on peut écrire :
C’est la troisième identité remarquable que nous pouvons écrire sous sa forme factorisée :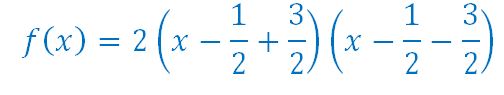
soit :
Résolvons :
C’est une équation produit. 
On obtient deux solutions :
Ces deux solutions appelées aussi racines sont les points d’intersection F et I de la parabole avec l’axe des abscisses.
REMARQUE
En connaissant les deux racines on peut factoriser :
Equation du second degré
Factorisation de l'équation
On applique le même principe que précédemment. Nous allons reproduire les calculs sans trop d’explication à partir de la forme générale d’une équation du second degré. 
On met a en facteur :
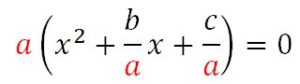
Les deux premiers termes de la parenthèse sont le début d’une identité remarquable. (Voir ci dessus).
On ajoute le carré du deuxième nombre de cette identité et on le retranche immédiatement pour ne pas changer la valeur de l’équation. 
On écrit l’identité sous forme factorisée et je réduis au même dénominateur les deux derniers termes du crochet:
On continue les calculs :
On ne peut prendre la racine carrée d’un nombre dans ℜ que s’il est positif.
Désignons par :
Ce nombre Δ (lettre grecque delta) est appelé discriminant. Si 
On peut prendre la racine carrée de Δ et on peut écrire en factorisant :
On obtient une équation produit et donc deux solutions appelées racines de l’équation. 
Si 
La racine carrée est nulle et 
Si 
On ne peut pas prendre la racine carrée de Δ Il n’y a pas de solution ou racine dans ℜ
Exemple numérique
Soit l’équation :
Et si on mettais 2 en facteur.
Rappel : lorsqu’on met un nombre en facteur, il faut évidemment diviser tous les nombres qui seront entre parenthèse par ce facteur. 
Les deux termes en rouge correspondent au début d’une identité remarquable développée : premier terme eu carré plus double produit. Il faut trouver le deuxième terme au carré.
Lorsqu’on l’a trouvé, on le rajoute pour faire apparaître l’identité développée mais on l’enlève tout de suite bien sûr pour ne pas changer l’équation. 
On écrit l’identité remarquable sous forme factorisée. ET en même temps comme dirait notre Président, on réduit au même dénominateur les deux derniers termes de la parenthèse.
On continue les calculs.
Voir la suite dans la seconde colonne.
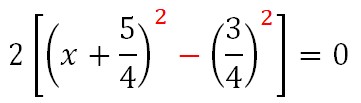
On aboutit à une différence de deux carrés qui est la troisième identité remarquable développée. On la factorise. 
Bien sûr on réduit.
C’est une équation produit. “Pour qu’un produit de facteurs soit nul, il faut et il suffit qu’un de ses facteurs soit nul”.
Et on trouve les deux solutions qu’on appelle racines. 
Connaissant les deux racines, on peut factoriser : 
Et voilà. C’est fastidieux. Pour aller plus vite on applique les formules trouvées avec la factorisation littérale.
Résolution pratique
On utilise bêtement les formules trouvées ci-dessus.
La forme générale est :
On calcule le discriminant Δ :
Si Δ>0 on calcule deux racines :
qu’on peut retenir sous cette forme :
Si Δ=0 on obtient une racine :
Si Δ<0 il n’y a aucune racine dans l’ensemble des réels. Mais il y en a deux dans l’ensemble des complexes.
Premier exemple :
Comme Δ>0 on a pu calculer sa racine carrée. Et l’équation possède deux racines.
Deuxième exemple :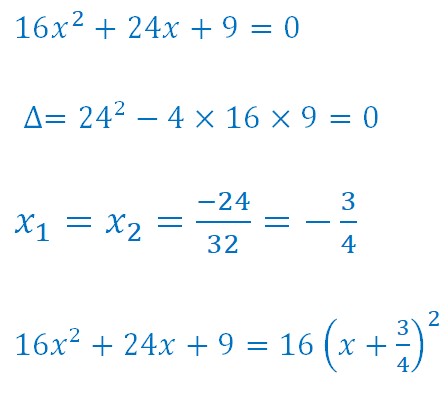
Δ était égal à 0. On a donc une seule racine double.
Troisième exemple :
Δ < 0 il n’y a donc pas de racine
Signe du trinôme du second degré
On appelle trinôme du second degré une expression algébrique de trois termes de la forme ax²+bx+c
Il s’agit ici de déterminer le signe de ce trinôme en fonction des valeurs de x.
La formule générale du trinôme ressemble à celle d’une équation.
On peut calculer le discriminant Δ qui va nous indiquer si ce trinôme s’annule pour certaines valeurs de x
Si
Le trinôme s’annule pour deux valeurs de x :
On peut factoriser :
et établir un tableau de signes : 
Nous en déduisons que le trinôme est du signe de a (coefficient de x) pour les valeurs de x situées en deçà de la plus petite racine et au delà de la plus grande, et du signe contraire de a (-a) pour les valeurs comprises entre les racines.
Si
On obtient une identité remarquable 
On peut dresser un tableau de signe :
Si
dans l’expression ci-dessous, ce qui est entre crochet est obligatoirement positif. 
Don le trinôme est du signe de a quelle que soit la valeur de x.
On se sert du signe du trinôme en général pour résoudre des inéquations du second degré. Prenons trois exemples.
Exemple 1 :
soit l’inéquation :
soit : 
Pour savoir si ce trinôme possède des racines, on calcule le discriminant Δ :
Ce trinôme a deux racines (il est égal à 0 pour deux valeurs de x) :
On dresse le tableau de signe : 
On en déduit les solutions de cette inéquation : 
Exemple 2 :
Soit : 
Calculons Δ :
Δ est égal à 0 donc le trinôme ne s’annule que pour une valeur de x :
et il est du signe de a : il est donc positif quelles que soient les valeurs de x.
Ce qui est tout à fait normal puisque ce trinôme peut s’écrire sous forme du carré d’une somme (identité remarquable) et un carré est toujours positif :
Exemple 3 
Soit le trinôme :
On calcule Δ :
Il est négatif, il n’existe pas de valeur de x qui annulent le trinôme. Il est donc du signe de a :
A>0, le trinôme est toujours positif quelles que soient les valeurs de X.
L’inéquation n’admet aucune solution. 
Somme et produit des racines d'une équation
Soit la forme générale d’une équation du second degré :
Nous savons calculer le discriminant de cette équation :
Et si ce discriminant est positif, nous savons calculer les deux racines :
Effectuons la somme de ces deux racines :
Les deux fractions étant au même dénominateur, on ajoute les numérateurs. 
On annule évidemment les racines de delta.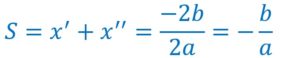 
On a ainsi trouvé la valeur de la somme des deux racines.
Passons au produit. 
On multiplie les numérateurs entre eux ainsi que les dénominateurs. 
On distribue le numérateur :
On réduit :
On remplace delta par sa valeur :
On calcule :
On réduit 
On simplifie ;
On obtient la valeur du produit des deux racines.
Formules à connaître : 
Reprenons la forme générale de l’équation du second degré :
factorisons par a :
Et d’après la somme et le produit des racines que nous venons de calculer, nous obtenons une autre forme d’équation générale du second degré : 
Avec une équation dont on calcule les racines, vérifions si la somme et le produit de ses racines sont bien égaux aux formules que nous avons trouvé. 
Existe-t-il deux nombres dont la somme est 4 et le produit 10 ?
Il s’agit de trouver deux nombres dont :
Soit l’équation générale du second degré :
Remplaçons S et P par leur valeur :
Calculons sont discriminant :
Le discriminant est négatif, l’équation n’a pas pas de solution dans ℜ.
Il n’existe pas de nombre réel dont la somme soit égale à 4 et le produit à 10.
Je dispose de 2 baguettes de bois de 10 cm servant à encadrer un tableau de 21 cm². Où dois-je couper chacune des baguettes pour qu’elles encadrent le tableau.
Raisonnons sur une seule baguette dont les morceaux encadrerons une longueur et une largeur du tableau.
Soient 
la longueur et la largeur du rectangle.
Leur somme est égale à la longueur d’une baguette soit 10 cm et leur produit est égal à la surface (aire) du rectangle.
Utilisons l’équation du second degré : 
Calculons son discriminant :
Il est positif, donc on aura 2 racines :
qui nous indique qu’on devra couper la baguette à 3 cm d’un bord et 
qui nous indique qu’on devra couper la baguette à 7 cm depuis l’autre bord.
Ce qui fait bien 1 m en tout et une aire de 21 cm².
Graphiques suivant les signes de a et delta
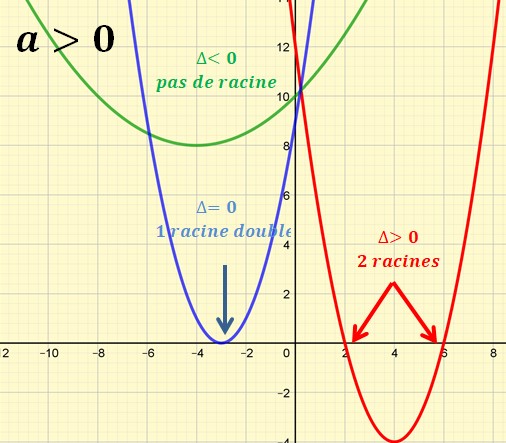
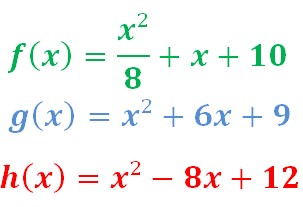
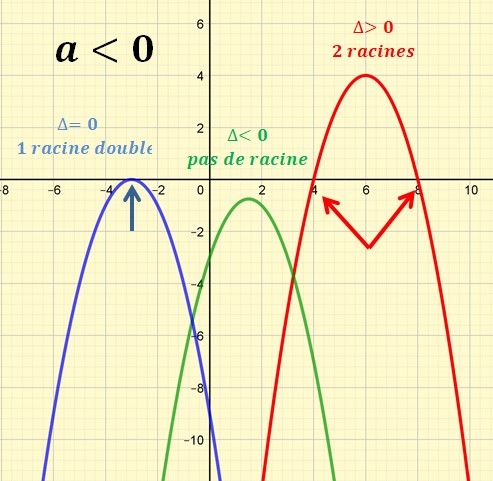
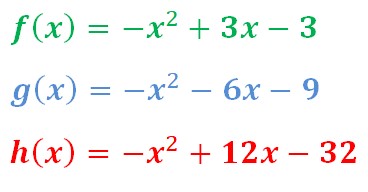
Un grand résumé graphique
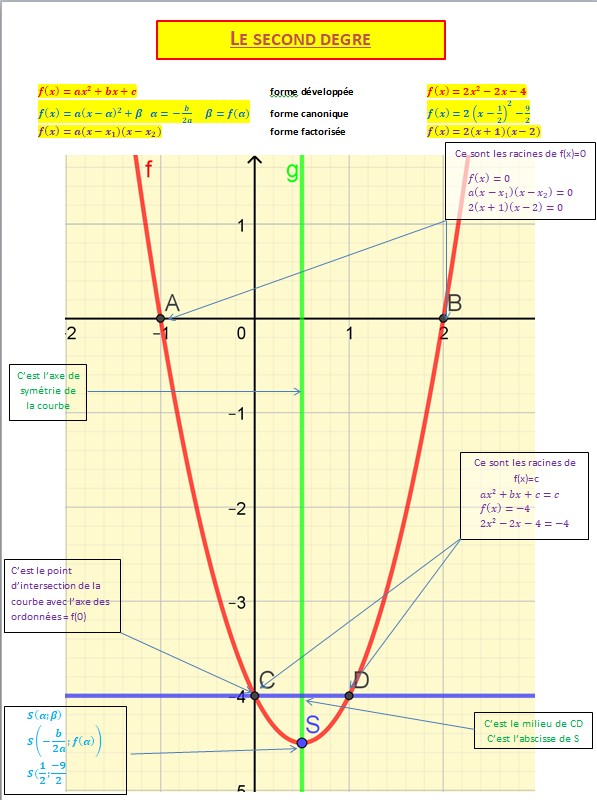
Quelques problèmes
Trouver la formule d’après le graphique
D’après le graphique, je connais les racines du trinôme (les points d’intersection de la courbe avec l’axe des abscisses, qui sont les résultats de l’équation f(x) =0.
Je connais aussi le point d’intersection de la courbe avec l’axe des ordonnées.
Je recherche quelle formule générale je vais pouvoir appliquer avec ces données pour trouver l’équation de la courbe.
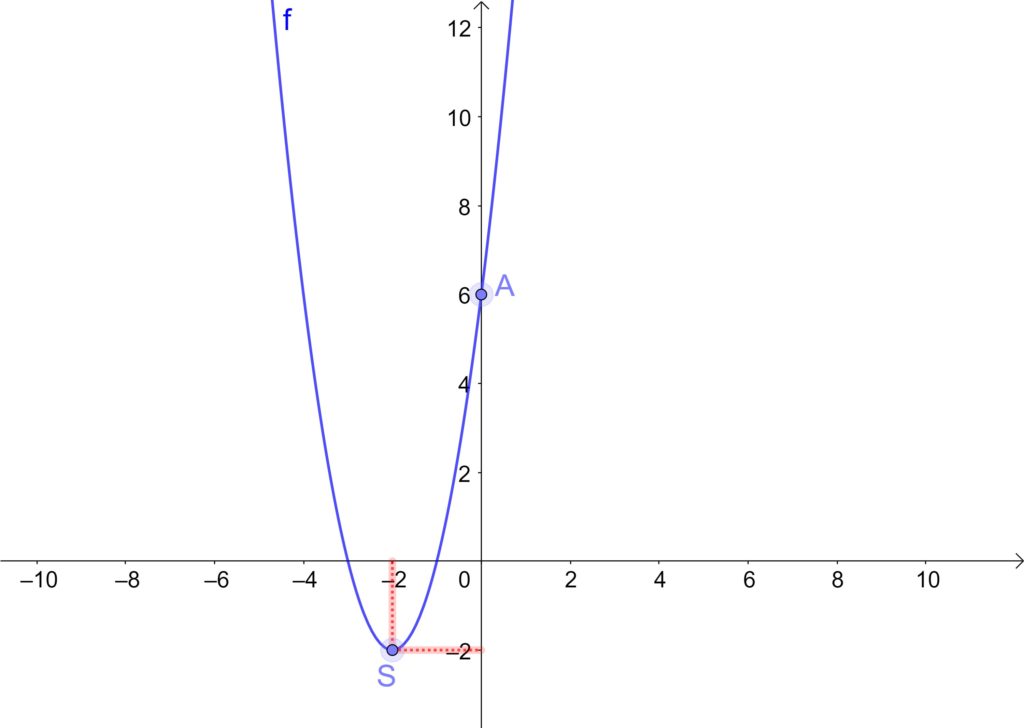
Je connais les coordonnées de l’extrémum de la courbe. Ici c’est un minimum. Je connais aussi le point d’intersection de la courbe avec l’axe des ordonnées.
Construire le graphique d’après des données.
On a intérêt à connaître le maximum de points pour construire la courbe. On peut utiliser l ‘axe de symétrie de la courbe.
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.
