Les suites
Généralités
Comme son nom l’indique, une suite est une suite de nombres écrits à la queue leu leu.
1;3;5;7;9;11;13………. est une suite. On peut même la définir comme la suite des entiers impairs. Les points de suspension indiquent que l’on peut continuer la suite à l’infinie.
En règle générale, mais ce n’est qu’une convention, on désigne les suites par les lettres U, V.
Le premier terme de la suite, ici 1 est désigné par U0 ou U1 Le petit 0 ou le petit 1 toujours placé en bas à droite de la lettre désignant la suite est appelé indice. Il indique la position du nombre, ou plutôt du terme dans la suite.
L’indice général du terme d’une suite est n. Ainsi Un est le nième ou le (n-1) ième terme de la suite suivant qu’on ait commencé par U1 ou U0
Voyons ce que ça donne dans un tableau :
Si U0 ; (n=0) est le premier terme qui vaut 1 : U0=1
Le deuxième terme est U1 ; (n=1) qui vaut 3. U1=3
Le troisième terme est U2 ; (n=2) qui vaut 5. U2=5
Le nième terme est Un-1 ; (n-1) qui a une valeur inconnue.
Le (n+1)ième est Un qu’on ne connaît pas.
MAIS
Si U1 ; (n=1) est le premier terme qui vaut 1 : U1=1
Le deuxième terme est U2 ; (n=2) qui vaut 3. U2=3
Le troisième terme est U3 ; (n=3) qui vaut 5. U3=5
Le nième terme est Un ; (n) qui a une valeur inconnue.
Le (n+1)ième est Un+1 qu’on ne connaît pas.
Il faut bien faire attention à ne pas confondre la position du terme dans la suite donnée par Un avec la valeur de ce terme.
n est un entier naturel variant de 0 à ∞. Il est évident qu’on ne va pas prendre un terme de rang 2,5 dans la suite.
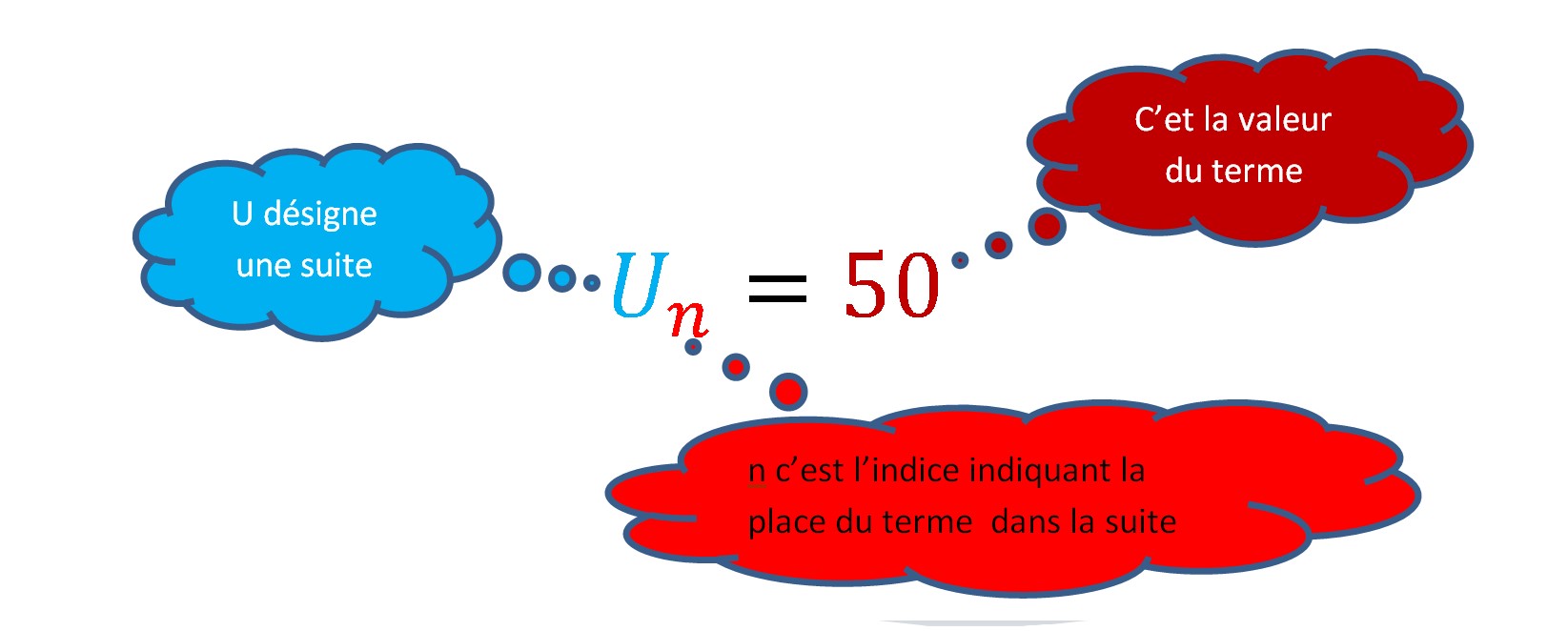
Le nième terme de la suite U vaut 50.
Les indices
Soit U la suite des nombres pairs. U0=2
| 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 |
| U0 | U1 | U2 | U3 | U4 | U5 | U6 | U7 | U8 | U9 |
Si je désigne le 6ième terme U5=12 par Un,
alors le terme précédent U4 sera Un-1
et le terme suivant U6 sera Un+1 
Deux façons de définir une suite
Formule par récurrence
Récurrence signifie retour, répétition. On revient en arrière et on répète.
Pour une suite cela consiste à calculer un terme d’après le terme précédent que l’on connaît et ainsi de suite.
Soit la suite définie par les formules :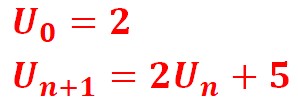 
Cela signifie que le terme de rang n+1 est égal à deux fois le terme précédent de rang n plus 5.
Je connais U0, je peux calculer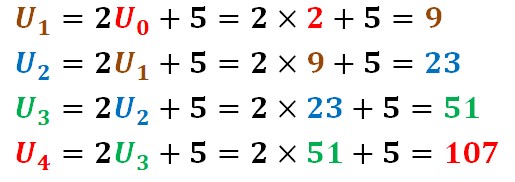 
On peut ainsi calculer de proche en proche n’importe quel terme pourvu que l’on connaisse son précédent.
Si je veux connaître la valeur du terme de rang 2019, il me faut calculer de proche en proche les 2018 termes précédents.
Ce serait inhumain !
Pourtant certains l’on fait avant nous et sans calculatrice !
Si c’est fastidieux pour un homme, par contre un ordinateur aime ça.
Essaye d’imaginer un algorithme pouvant calculer le terme de rang 2019.
Formule explicite
Une formule explicite est une formule qui permet de calculer un terme en fonction de son rang. Ainsi on peut calculer directement Un à partir de n.
On n’a même pas besoin de connaître le premier terme.
Soit la suite définie par la formule explicite suivante : 
Cela signifie que le terme de rang n est égal à 4 fois son rang moins 2.
A partir de cette formule explicite, je peux calculer n’importe quel terme facilement.
Allons y pour les 5 premiers termes :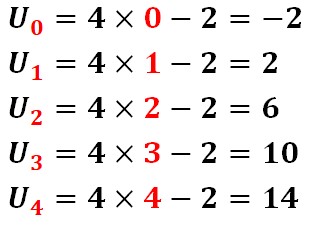
On peut même calculer le terme de rang 2019 :