Nombre dérivé
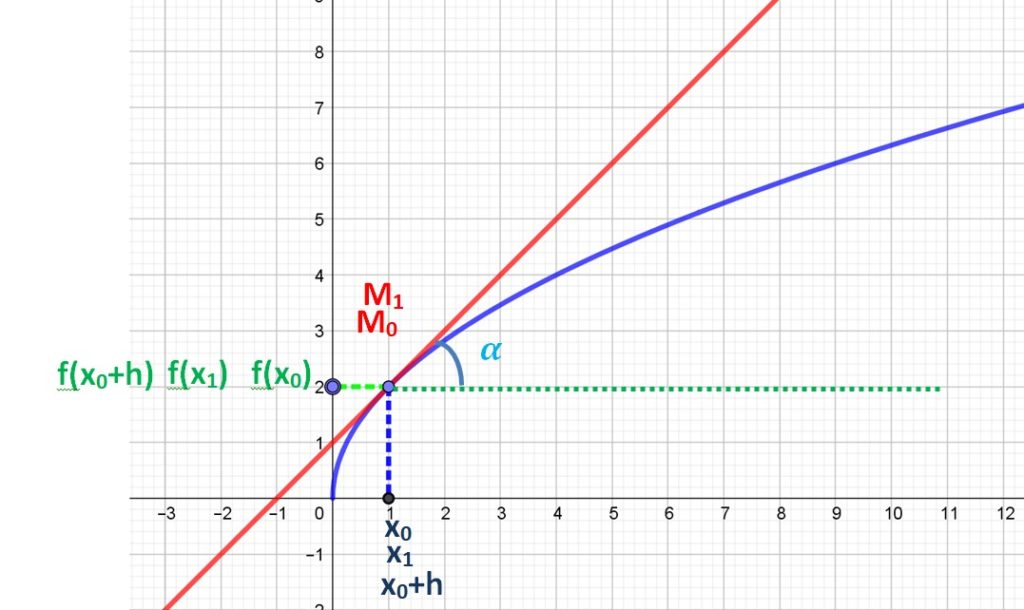
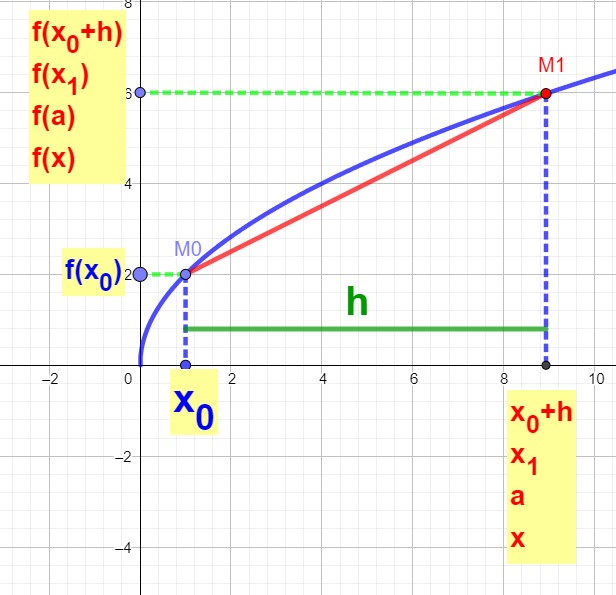
Une fonction, une courbe représentative, deux points, une corde
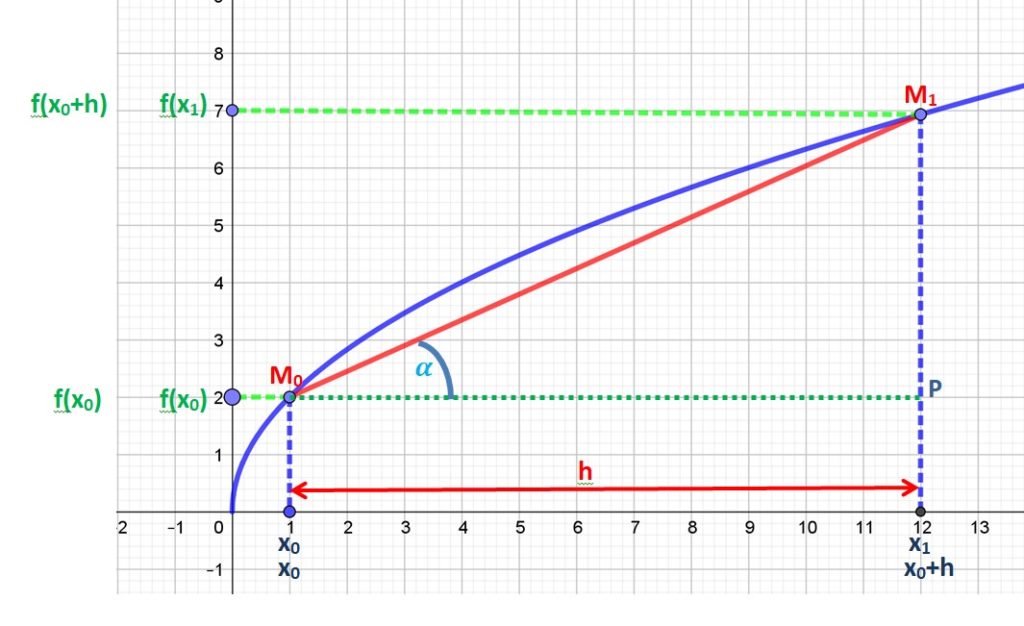
Soit deux points M0 et M1 pris sur la courbe représentative de la fonction f(x).
Le point M0 a pour abscisse x0 et pour ordonnée f(x0).
Le point M1 a pour abscisse x1 et pour ordonnée f(x1).
Lorsqu’on joint ces deux points, on obtient une corde, segment de droite sous l’arc de la courbe bleues) M0M1.
Taux d'accroissement
M1 se rapproche de M0
Nous avons vu dans le chapitre “taux d’accroissement” ou taux de variation que ce taux était défini par :
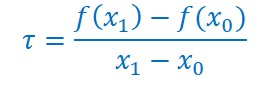Cet accroissement correspond à la pente ou coefficient directeur de la droite M0M1. Le triangle M1PM0 étant rectangle le taux d’accroissement correspond aussi à la tangente de l’angle α.
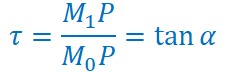
Autre manière de présenter ce taux d’accroissement.
Soit h l’accroissement des x, la distance entre x0 et x1, la différence x1-x0
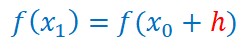et le taux d’accroissement s’écrira :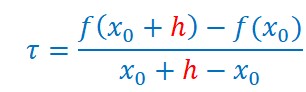 
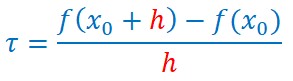
Explication détaillée
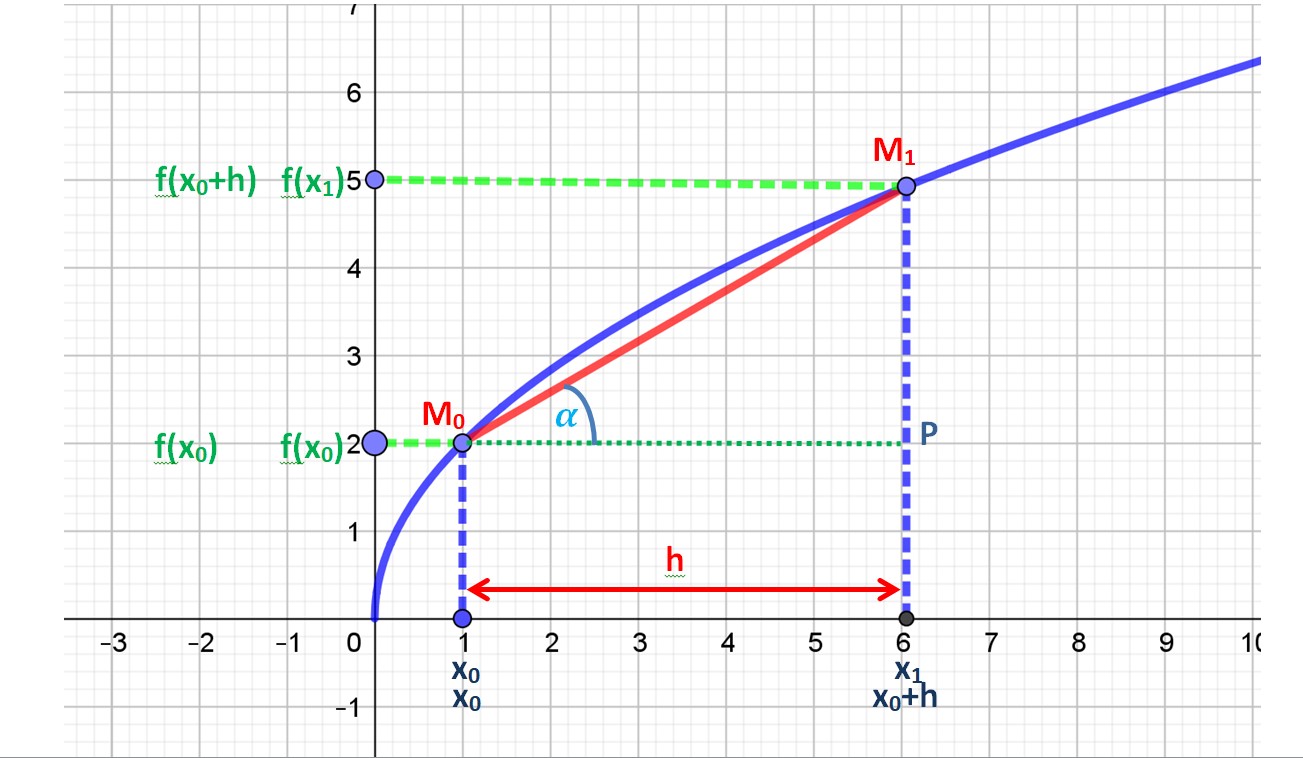
Dans le graphique ci contre, le point M1 se rapproche de Mo en glissant sur la courbe.
La longueur de la corde M0M1 diminue.
x1 se rapproche de x0.
La distance h entre x1 et x0 ou x0+h et x0 diminue.
De ce fait le taux d’accroissement change.
Ainsi que la pente ou coefficient directeur de la corde.
Et donc aussi l’angle α
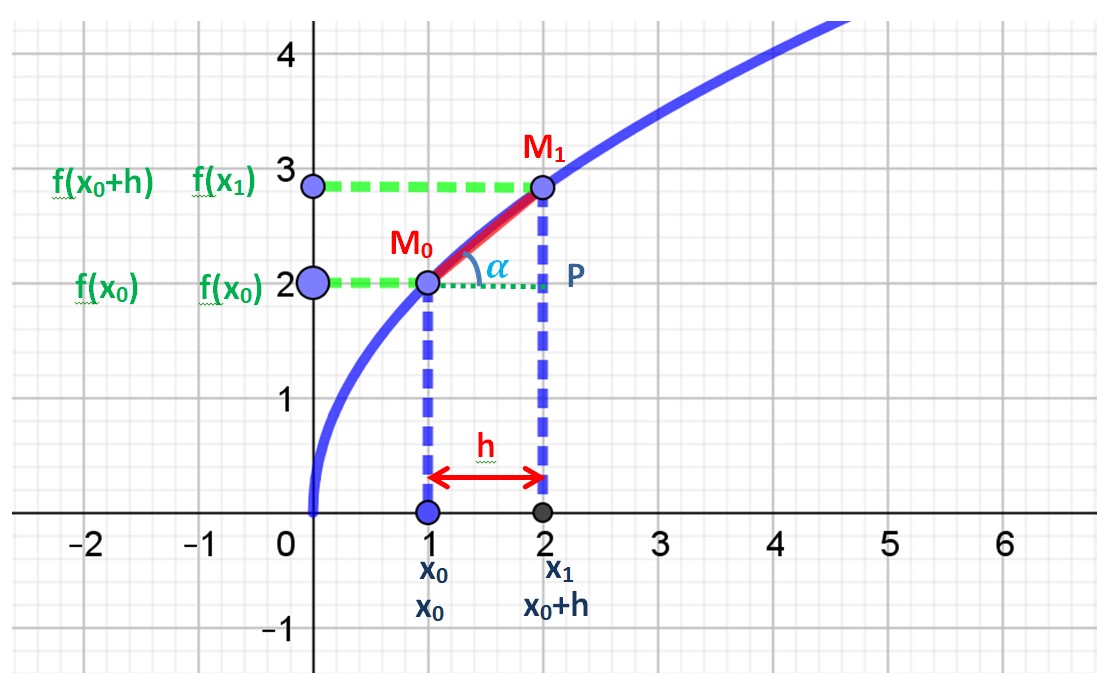
Le processus continue.
le point M1 se rapproche de Mo
La longueur de la corde M0M1 diminue et se rapproche de 0
x1 se rapproche de x0.
La distance h entre x1 et x0 ou x0+h et x0 diminue et se rapproche de 0 aussi.
De ce fait le taux d’accroissement change.
Ainsi que la pente ou coefficient directeur de la corde.
Et donc aussi l’angle α.
Là c’est la fin
M1 se confond pratiquement avec M0
On dit que M1 tend vers M0
Donc x1 tend vers x0. Il ne peut pas se confondre avec x0 car x1-x0 serait nul et on ne pourrait pas calculer le taux d’accroissement, la division par 0 étant impossible.
De même h la distance entre x0 et x1 tend vers 0 sans jamais s’annuler sinon………
M1 et M0 étant pratiquement confondus, la corde ne coupe plus la courbe qu’en un point.
C’est une tangente à la courbe.
Le taux d’accroissement calculé à partir de x0 est le nombre dérivé de la courbe au point d’abscisse x0 et le coefficient directeur ou pente de la tangente en ce point.
Définition du nombre dérivé
Une fonction f est dérivable en un point x0 si et seulement si le nombre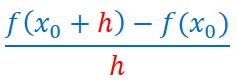 
a pour limite un nombre fini l lorsque h tend vers 0.
l est appelé nombre dérivé de la fonction en x0.
On le nomme f'(x0) et on écrit :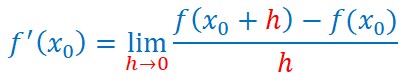
Cette définition traduit de manière concise tout ce que nous venons de voir précédemment à partir du taux d’accroissement, appelé parfoix taux d’accroissement moyen ou taux de variation.
Parfois on utilise la notation a au lieu de x0, mais c’est la même chose.
La dernière formule se lit en français :
Le nombre dérivé d’une fonction en un point x0 (ou a) est la limite lorsque h tend vers 0 du nombre
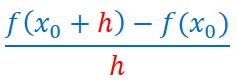
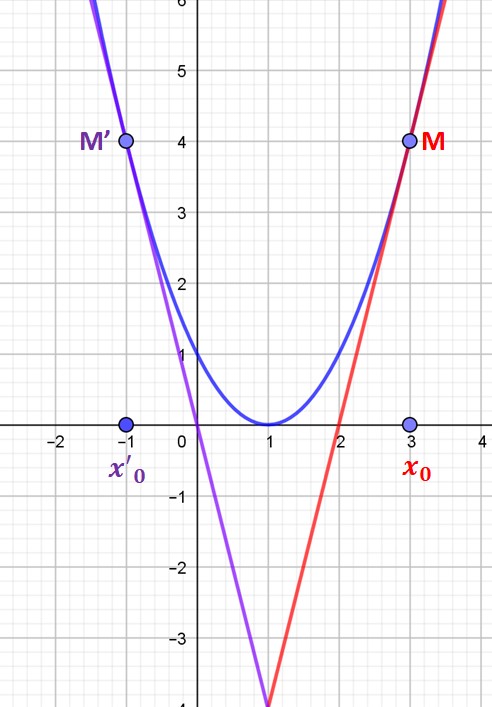
Exemple
Soit la fonction :
Calculer le coefficient directeur de la tangente au 
et au 
On a deux possibilités de calcul. Soit on effectue le calcul en remplaçant dés le début x0 par sa valeur 3, soit on calcule tout du long avec x0 que l’on remplacera par sa valeur 3 à la fin.
Calcul avec 3.
Nous savons que le coefficient directeur de la tangente à une courbe en un point est le nombre dérivé en ce point, nombre qui nous est donné par la formule :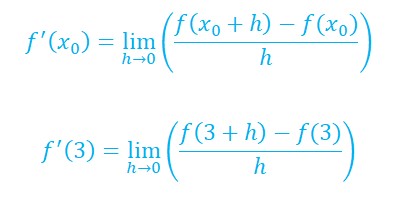
Il suffit de remplacer x0 par sa valeur 3.
On calcule f(3+h) et f(3)
Attention :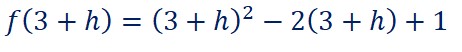
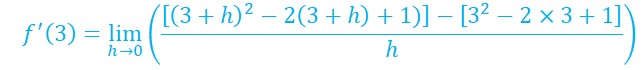
On continue les calculs :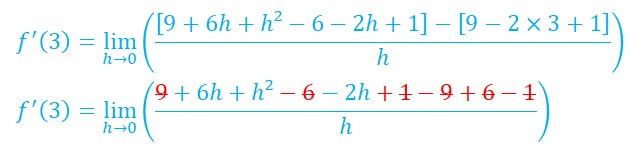
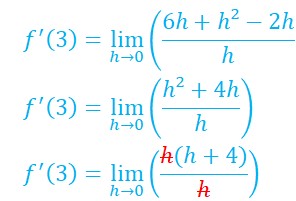
On peut simplifier par h car h tend vers 0 sans jamais atteindre cette valeur; h est différent de 0.
Comme on parle de limite; h + 4 tend vers 0+4 quand h tend vers 0. Donc : 
On peut vérifier sur le graphique grâce aux carreaux que le coefficient directeur de la tangente en M à la courbe est bien 4.
Calcul avec xo.
On garde tout au long du calcul x0
On revient à la formule du nombre dérivé et ensuite ce ne sont que calculs.
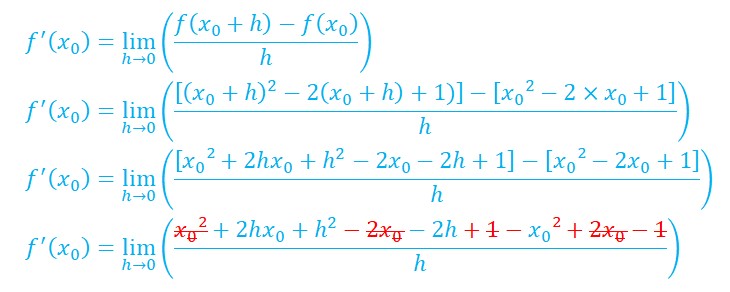
Pour x0=3 on trouve bien f'(3)=4.
Pour x0=-1 on trouve f'(-1)=-4 que l’on vérifie bien sur le graphique.
Ainsi, en général à chaque point de la courbe on peut trouver un nombre dérivé qui correspond au coefficient directeur ou pente de la tangente en ce point.
Ce sera le sujet d’un chapitre sur les fonctions dérivées.
Différentes formules du nombre dérivé
Toutes ces formules ne sont pas exhaustives. On peut en rencontrer d’autres .
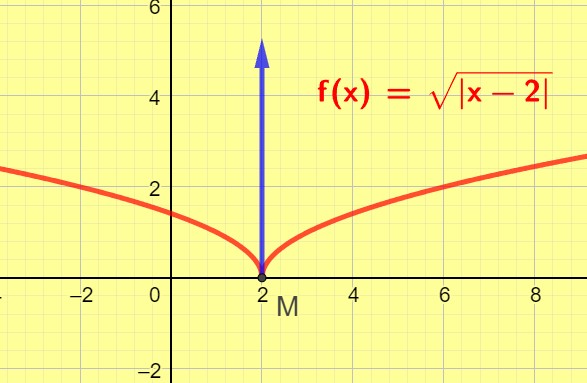
Dérivabilité et continuité.
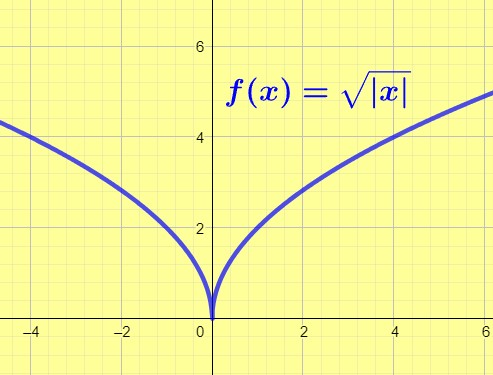
Cette fonction est continue en x=0 car :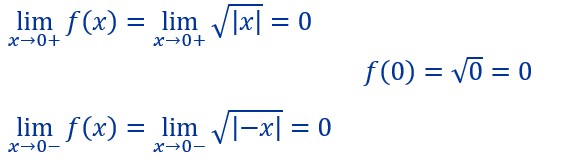
Mais elle n’est pas dérivable en x=0, en effet :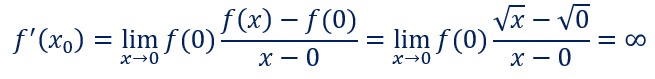
Ce n’est pas une valeur finie.
Attention la réciproque est fausse : une fonction continue en x0 n’est pas forcément dérivable en ce point.
Voir les exemples ci contre.
Dérivabilité à droite et à gauche
Dérivée à droite
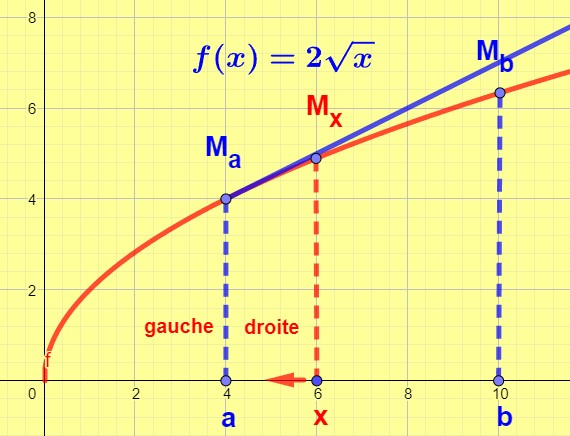
Nombre dérivé pour a=4: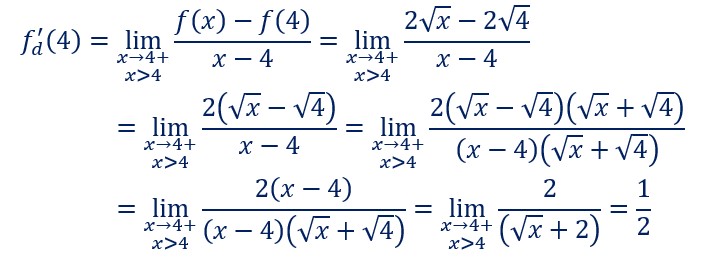
La demie tangente en Ma a donc pour coefficient directeur 0,5.
Soit la fonction 
Etudions la dérivée au point Ma d’abscisse a sur l’intervalle [a;b]
x tend vars a d’une seule façon de droite vers la gauche, x est à droite de a. x est plus grand que a On calculera la dérivée à droite de a qu’on écrira :
Au point Ma on construira une demi-tangente dont la pente ou coefficient directeur sera égal à cette dérivée au point a
Dérivée à gauche
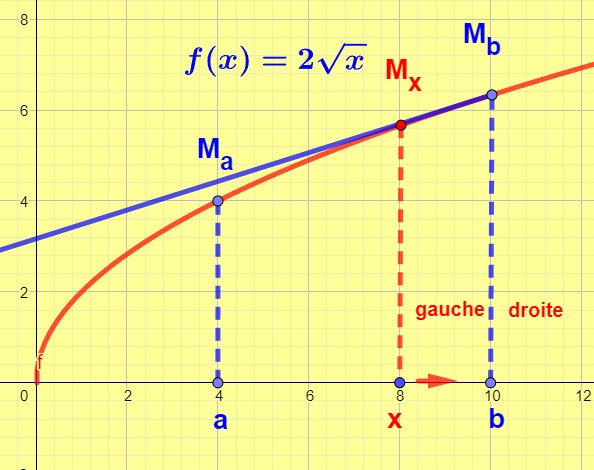
Nombre dérivé pour b=10
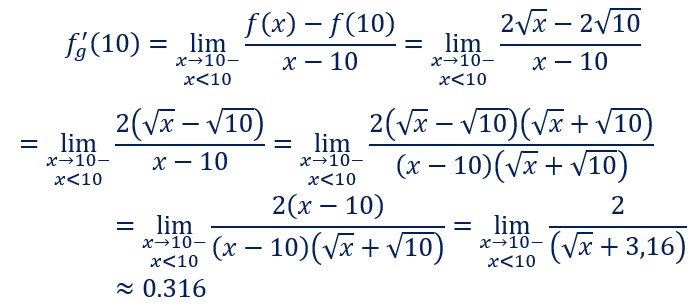
La demie tangente au point Mb a donc pour coefficient directeur 0,316
Soit la fonction
Etudions la dérivée au point Mb d’abscisse b sur l’intervalle [a;b]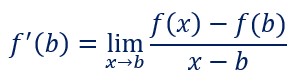
x tend vars b d’une seule façon de gauche vers la droite, x est à gauche de b. x est plus petit que b On calculera la dérivée à gauche de b qu’on écrira :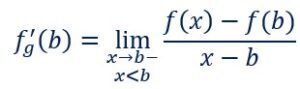
Au point Mb on construira une demi-tangente dont la pente ou coefficient directeur sera égal à cette dérivée au point b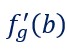
Dérivabilité à droite et à gauche
En déplaçant le point Mt ou l’abscisse t avec la souris, on voit que la dérivée à gauche est égale à -1 et la dérivée à droite est égale à 1. Par contre lorsque t est en 0 la dérivée f’ est indiquée avec un point d’interrogation pour montrer qu’elle n’existe pas.
Equation de la tangente
Cette animation donne l’équation de la tangente en un point M0 de la courbe d’abscisse x0. Pour modifier le point Mo, il suffit de faire varier le curseur x0 situé en haut.
Autre démonstration de l’équation de la tangente qui est un excellent moyen de s’en souvenir si on connait la formule du taux d’accroissement.
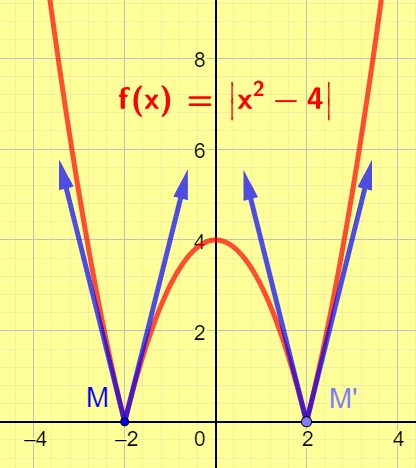Cette fonction admet deux demies tangentes en chacun des points M et M’ d’abscisses respectives -2 et 2.
Chaque point M et M’ est également un point anguleux.
Approximation affine
Si ce n’est fait, positionner le curseur sur e=0. Puis le faire glisser successivement sur 1,2, jusqu’à 5 en lisant chaque fois les légendes sur la colonne de droite.
Positionner le curseur sur e=6 et continuer jusqu’à 9.
On s’accroche , on se concentre, c’est indispensable pour comprendre la suite.
e= 1 Soit une fonction quelconque f dont la courbe est représentée en rouge sur le graphique ci-contre.
Soit un point M0 de cette courbe de coordonnées x0 et f(x0).
e=2 On trace la tangente T à la courbe au point M0
e=3 Soit un point M de la courbe de coordonnées x et f(x) situé au voisinage de x0. Le point P a pour coordonnées x et 0. C’est la projection du point M sur l’axe des abscisses.
le but est d’obtenir l’ordonnée du point M c’est-à-dire la valeur de f(x) ou encore la longueur du segment PM sans appliquer la formule de la fonction.
e=4 le point O a pour coordonnées x et f(x0).
le point N situé sur la tangente T a pour abscisse x, son ordonnées est en J.
Les autres points I,J,K,L permettent de mieux se repérer pour la suite.
e=5 Comme le coordonnées de O sont x et f(x0) le segment PO a pour longueur f(x0).
e=6 Considérons le triangle M0ON. Il est rectangle. La tangente de l’angle α est le coefficient directeur de la tangente à la courbe ( en bleu) et c’est aussi le nombre dérivé en x0 de la courbe.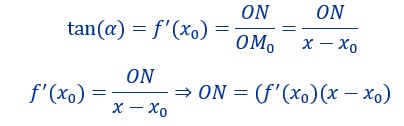 
e=7 Il reste à calculer un résidu, la longueur du segment NM. Soit la droite passant par L d’abscisse x0 et par M d’abscisse x. Cette droite est une fonction affine dont le coefficient directeur que l’on nommera ε(x) est aussi la tangente de l’angle β. Le triangle LMN est rectangle en N. On peut donc écrire :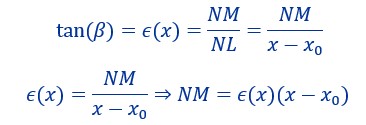
e=8 Rien ne se passe. Erreur de ma part.
e=9 On obtient ainsi le formule qui donne la valeur de f(x), l’ordonnée de M sans passer par la formule de la fonction, en utilisant uniquement deux fonctions affines plus un nombre dérivé.