Notion de limites
La définition du Robert est celle-ci : grandeur fixe dont une grandeur variable peut approcher indéfiniment sans jamais l’atteindre. Voyons en quoi cela consiste.
La division par 0
On apprend depuis le CM2 que la division par 0 est interdite. En fait ce n’est pas interdit de diviser par 0 mais ça n’a pas de sens. Partager un sac de 100 billes entre 0 enfant est insensé, c’est absurde.
Mais rien n’empêche de diviser par un nombre qui est proche de 0.
C’est ce que nous allons faire.
Sur la droite ci-dessus, on a représenté des nombres et 0.
On voit que le nombre le plus à droite est 0.1. Puis en allant vers la gauche on trouve le nombre 0,01. En continuant on trouve 0,001 puis 0,0001
Avec ces nombres on s’approche de plus en plus vers 0.
Si on prend un nombre x sur cette droite et qu’on lui donne successivement les valeurs 0,1; 0,01; etc
x s’approche de plus en plus de o sans jamais l’atteindre. On dit que x tend vers 0.
Diviser par exemple 1 par 0, nous l’avons vu n’a aucun sens. Mais voyons ce qui se passe lorsque nous divisons 1 par x qui tend vers 0.
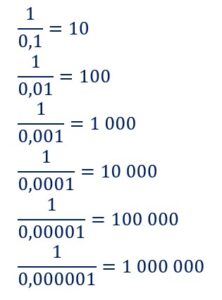
→Quand x tend vers 0 on voit que devient de plus en plus grand. Si on continue sur cette lancée, on aura des nombres d’une grandeur astronomique. On dit que 1 sur x tend vers plus l’infini que l’on note :
1/x→+∞
x tend vers 0 à droite
Dans l’animation ci-dessous, le nombre X prend successivement des valeurs allant de 0,1 à 0,001.On voit qu’il s’approche de plus en plus de 0 mais il ne l’atteint pas. On dit que X tend vers 0. Tendre signifie s’approcher de plus en plus d’un but sans jamais l’atteindre.
Dans ce cas, X est à droit du 0, X est positif.
On dit que X tend vers 0 à droite ou bien x tend vers 0 par valeurs positives.
Clique sur le logo en bas à gauche du graphique pour lancer l’animation .
x tend vers 0 à gauche
Dans l’animation ci-dessous, le nombre X prend successivement des valeurs allant de -0,1 à -0,001.On voit qu’il s’approche de plus en plus de 0 mais il ne l’atteint pas. On dit que X tend vers 0. Tendre signifie s’approcher de plus en plus d’un but sans jamais l’atteindre.
Dans ce cas, X est à gauche du 0, X est négatif.
On dit que X tend vers 0 à gauche ou bien x tend vers 0 par valeurs négatives.
On constate que lorsque l’abscisse B du point A tend vers l’infini, son ordonnée
Limites de la fonction inverse quand x tend vers 0
Soit la fonction
Elle est représentée en vert sur le graphique animé ci-dessous. Elle n’est pas définie pour x=0. Mais on peut se rendre compte de son comportement quand x tend vers 0.
L’abscisse B du point A en rouge tend vers 0 à droite, par valeurs positives. A côté du point A sont notés son abscisse et son ordonnée.
Il en est de même de l’abscisse B’ du point A’ en bleu, mais qui tend vers 0 à gauche par valeurs négatives.
En cliquant sur la flèche en bas à gauche du graphique on se rend compte des comportements des points A et A’ .
Ainsi nous voyons que :
lorsque x tend vers 0 par valeurs positives f(x) tend vers +∞ car 1 divisé par un très petit nombre positif donne un très grand nombre positif qui peut atteindre une valeur immensément grande .
lorsque x tend vers o par valeurs négatives f(x) tend vers -∞ car 1 divisé par un très grand nombre négatif donne un très petit nombre négatif qui peut atteindre une valeur infiniment petite.
limite de la fonction inverse quand x tend vers plus l'infini
Lorsque l’abscisse B du point A tend vers +∞ f(x) l’ordonnée du point A tend vers 0 par valeurs positives.
Limite de la fonction inverse quad x tend vers moins l'infini
LOrsque l’abscisse B du point A tend vers -∞, f(x) l’ordonnée du point A tend vers 0 par valeurs négatives.
Limites : définitions
Limite infinie à l’infini :
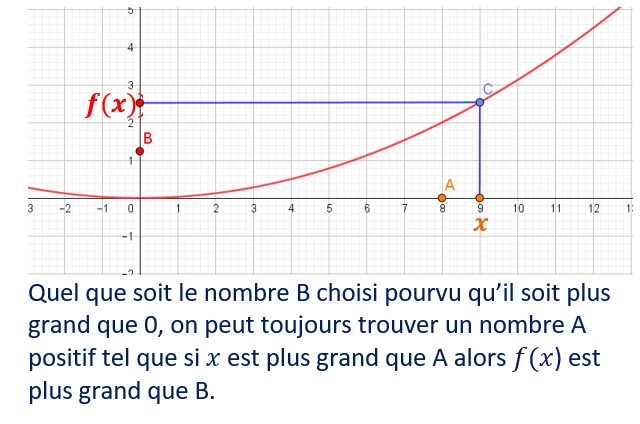
Limite finie à plus l’infini
Définition de la limite finie l d’une fonction lorsque la variable x tend vers +∞ :
Pour que la limite l existe, il faut :
se donner un nombre positif ε de telle façon que l’image f(x) de x par f soit comprise entre l-ε et l+ε, ce qui traduit que la valeur absolue de f(x)-l est comprise entre 0 et ε.
A partir de là, il nous faut trouver un nombre α positif de telle façon que x soit plus grand que α. En d’autres termes x tend vers l’infini.
Quan x tend vers +∞, f(x), en rouge se situe bien entre les droites d’équation l-ε et l+ε.
Exemple :
Soit la fonction : 
représentée graphiquement ci-contre.
Dire que f(x) tend vers la limite l quand x tend vers l’infini, peut se traduire par la valeur de la fonction f(x) se situe entre les deux droites verts l-ε et l+ε. ε étant un nombre positif.
Cela peut se traduire aussi de cette manière : la distance entre la valeur de f(x) et la limite l est comprise entre l-ε et l+ε. Deux façons d’écrire mathématiquement cette phrase :
En prenant la seconde façon, on remplace f(x) par sa valeur et l par 4 la limite de f(x) :
Comme x tend vers +∞ 
Donc on peut multiplier les membres des inéquations précédentes par x-1 sans changer le sens des inéquations. 
On obtient deux inéquations qu’on développe :
Ensuite il suffit de continuer à calculer :
On obtient deux valeurs. Puisque ε est positif par hypothèse, l’une est négative et l’autre positive. x étant aussi positif, x plus grand qu’une valeur négative n’est pas surprenant. Mais x doit être plus grand que la valeur positive et en même temps plus grand que α.
Donc quel que soit le nombre positif ε choisi arbitrairement, on peut trouver le nombre α positif qui est égal à :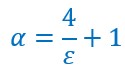
.
La fonction f(x) tend bien vers l=4
La droite d’équation y=l, y =4 dans notre exemple est appelée asymptote . Elle détermine la limite de la fonction quand celle-ci tend vers + l’infini. La fonction s’approche indéfiniment de l’asymptote sans jamais l’atteindre. Dans ce cas il s’agit d’une asymptote horizontale.
Limite finie à moins l’infini
Nous avons une définition analogue en tenant compte du fait que x tend cette fois vers moins l’infini. 
En prenant la même fonction que précédemment,
on traduit la valeur absolue :
comme le dénominateur est négatif, en multipliant par ce dénominateur, il nous faut changer le sens des inéquations.
On obtient un nombre α négatif.
La droite d’équation y=l, y =4 dans notre exemple est appelée asymptote . Elle détermine la limite de la fonction quand celle-ci tend vers – l’infini. La fonction s’approche indéfiniment de l’asymptote sans jamais l’atteindre. Dans ce cas il s’agit d’une asymptote horizontale.
Limite infinie en un point
Nous nous limiterons (Sans jeu de mots ) aux énoncés. 
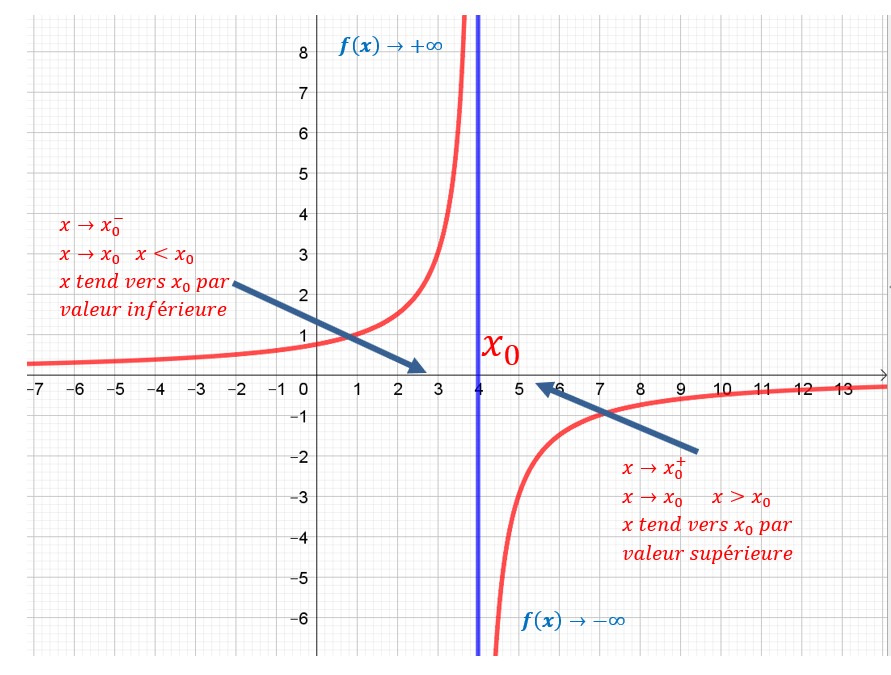
Il est difficile de ne pas faire d’erreurs dans ce méli mélo de conditions et de conclusions.Veuillez m’excuser s’il y en a.
La droite d’équation x=x0, x =4 dans notre exemple est appelée asymptote . Elle détermine la limite de la fonction vers + ou – l’infini quand celle-ci tend vers x0. La fonction s’approche indéfiniment de l’asymptote sans jamais l’atteindre. Dans ce cas il s’agit d’une asymptote verticale.
Limites des fonctions usuelles
Plutôt que de retenir par coeur ces limites, le mieux est de se représenter la fonction soit mentalement soit sur le papier pour en déduire chacune des limites. 
D’autres limites à connaître qui peuvent être utiles pour d’autres calculs.
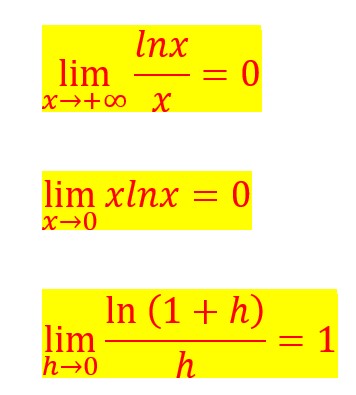
Théorèmes sur les limites
Ces théorèmes sont tout à fait logiques. Rien à retenir par coeur. 
Formes indéterminées.
Après le calcul de limites on peut obtenir des formes indéterminées qui ne permettrons pas de trouver la limite. Ces formes indéterminées sont les suivantes : 
Théorème de comparaison
Prenons le cas où deux fonctions sont voisines l’une de l’autre lorsque leur variable x tend vers plus l’infini.
Prenons le cas maintenant où deux fonctions sont voisines , mais leur variable x tend vers moins l’infini. 
Enfin, prenons le cas où les deux fonctions voisines tendent vers un point d’abscisse a :
Théorème des gendarmes
Sur l’animation ci-contre, il s’agit de trouver la limite de la fonction f(x). Cette dernière se trouve encadrée par deux fonctions g(x) et h(x) comme un voleur est encadré par deux gendarmes.
Placer le curseur α à l’extrémité gauche dont sa valeur est 0,5 environ. Le faire glisse lentement vers la droit. Aparaissent 4 points A, B, C D.
Le point A est l’image des abscisses. Il se déplace vers la droite. Il tend vers plus l’infini. Par commodité, il s’arrête au point d’abscisse 40.
Le point B se déplace sur la courbe g(x) en vert il tend vers 0– , par valeurs négatives.
Le point C se déplace sur la courbe h(x) en bleu et tend vers 0+, par valeurs positives.
On observe que le point D se déplace vers la droite sur la courbe rouge f(x). Il tend vers 0. Donc la limite de f(x) quand x tend vers + l’infini est 0.
Sur l’animation ci-contre, il s’agit de trouver la limite de la fonction f(x). Cette dernière se trouve encadrée par deux fonctions g(x) et h(x) comme un voleur est encadré par deux gendarmes.
Placer le curseur α à l’extrémité droite dont sa valeur est -0,5 environ. Le faire glisse lentement vers la gauche. Aparaissent 4 points A, B, C D.
Le point A est l’image des abscisses. Il se déplace vers la gauche. Il tend vers moins l’infini. Par commodité, il s’arrête au point d’abscisse -40.
Le point B se déplace sur la courbe g(x) en vert il tend vers 0+ , par valeurs positives.
Le point C se déplace sur la courbe h(x) en bleu et tend vers 0–, par valeurs négatives.
On observe que le point D se déplace vers la gauche sur la courbe rouge f(x). Il tend vers 0.Donc la limite de f(x) quand x tend vers moins l’infini est 0.
Limite d'une fonction composée
Exemple : Quelle est la limite de 
quand x tend vers 1 par valeurs positives, c’est-à-dire quand x tend vers 1 en restant toujours plus grand que 1.Ce qu’in peut écrire x tend vers 1+.
Nous avons une fonction composée de deux fonction f(x)=g(h(x)) ou f=gΟh.
ce qui peut se résumer de la façon suivante :
Calculons la limite de h(x) quand x tend vers 1.
Maintenant, il suffit de calculer la limite de g(X) quand X tend vers +∞.
Donc :
Voir le graphique ci-contre..
Asymptote oblique
Dans l’exemple ci-contre, la fonction est :
et la droite asymptote a pour équation y=x, avec a=1 et b =0
Règle le curseur α sur 1,5 environ. Le point C donne la valeur de x. Le point B se déplace sur la courbe rouge et le point A se déplace sur l’asymptote en même temps que C Pointe ta souris sur le point α du curseur et fait le glisser doucement vers la droite. Le point C se déplace vers la droite, on peut dire que x tend vers l’infini. (Pour des raisons d’espace il s’arête à 6. On voit le point B se rapprocher du point A. Le segment AB rétrécit et tend vers 0.
Tu règles ensuite le curseur avec α égal à environ -1,5. En déplaçant le curseur α vers la gauche C se déplace vers la gauche et x tend vers -∞. En fait il s’arête à -6. On observe que le segment AB tend également vers 0.
La longueur du segment AB est représentée par l’expression :
Nous allons démontrer que cette expression tend vers 0 lorsque x tend vers + ou – ∞
f(x)-x représente sur le graphique la longueur du segment AB.
Les calculs qui suivent se passent de commentaires ( niveau quatrième); Il suffit de réduire les fractions au même dénominateur à condition qua x soit différent de -1 et de 1.
Nous en déduisons que :
La limte du numérateur est +∞. La limite du dénominateur est également +∞. On tombe sur une forme indéterminée; Il faut lever cette indétermination.
Pour lever l’indétermination, nous allons mettre x² en facteur au dénominateur. (Voir ci-dessous les méthodes pour lever les indéterminations.). et nous pouvons simplifier par x à condition qu’il soit différent de 0, ce qui est le cas puisqu’on est dans l’intervalle 1;+∞ exclus. 
le numérateur tend vers 1. 1/x² tend vers 0 ( un nombre divisé par un très grand nombre); de ce fait le dénominateur tend vers +∞.
Donc la limite cherchée est 0. (un nombre divisé par un très grand nombre.