Suites arithmétiques
Approche intuitive
Représentation presque réelle de la situation :
Représentation dans un tableau :
Représentation plus théorique :
Je pratique un entraînement intensif à vélo. Le premier jour, je roule sur une distance de 5 km. Puis à partir du deuxième jour, j’augmente ma distance de 2 km chaque jour.
Je remarque que la distance parcourue en une journée quelconque est égale à la distance parcourue la veille plus un nombre fixe, toujours le même, 2.
Dans la première figure ci-contre, j’ai représenté mon entraînement comme il pourrait se passer dans la réalité,
J’ai ensuite résumé tout cela dans un tableau.
Pour terminer avec une suite
U1 représente la distance parcourue le jour 1
U2 représente la distance parcourue le jour 2
etc
Un représente la distance parcourue le jour n
Définition
Autrement dit :
Formule par récurrence (en fonction du terme précédent) :
Passage à une formule explicite (en fonction de n) :
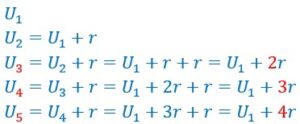
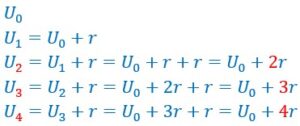
La définition donne une formule récurrente : on calcule les termes de la suite, de proche en proche. Un terme est égal au terme précédent plus la raison.
Avec cette formule par récurrence, il nous faut connaître le terme précédent celui dont on calcule la valeur.
Il est intéressant parfois de connaître chaque terme de la suite sans connaître le précédent, mais en fonction du rang n. Pour cela on part du premier terme 
ou 
.
A partir de U1, on clacule U2 par récurrence, on obtient U2 en fonction de U1. Puis on calcule U3 par récurrence en remplaçant U2 par sa valeur précédente en fonction de U1
on recommence de proche en proche. On s’aperçoit que le multiplicateur de r est égal à l’indice (ou rang) n de Un moins 1.
D’où la formule explicite si le premier terme est U1 .
On procède d’une façon semblable si le premier terme est U0. On obtient une formule différente.
En effet considérons le tableau ci-dessous :
Il indique l’indice d’un terme suivant que l’on commence par un indice 0 ou 1.
Reconnaître une suite arithmétique
Pour reconnaître une suite arithmétique, il suffit avec les formules explicites d’effectuer la différence entre un terme de rang n+1 et son précédent, le terme de rang n; Si cette différence est un nombre fixe, alors la suite est une suite arithmétique. 
Si le premier terme est U1
Si le premier terme est U0
Avec une formule par récurrence, point n’est besoin de faire des calculs, la réponse est évidente.
Exemples
La suite définie par la formuule explicite 
est-elle une suite arithmétique ?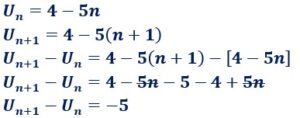 
-5 est une constante, ne varie pas quel que soit n. est une suite arithmétique.
—————————-
La suite définie par la formule explicite 
est-elle une suite arithmétique ?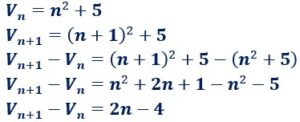 
2n-4 n’est pas une constante puisque n varie. Donc la suite n’est pas une suite arithmétique.
Propriétés
Croissance ou décroissance
Si la raison r d’une suite arithmétique Un est positive, la suite est croissante .
Si la raison r d’une suite arithmétique Un est négative, la suite est décroissante. 
La suite ci-dessous est croissante puisque sa raison est positive :
La suite ci-dessous est décroissante puisque sa raison est négative :
Trouver un terme Un à partir d’un autre Up sans passer par U0 .
n>p
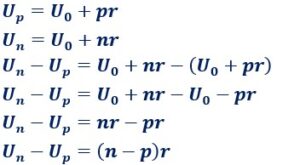
Quel est le 20ième terme d’une suite arithmétique de raison 4 et dont le 15ième terme est égal à 300.
Puisqu’on connaît un terme et la raison, on peut appliquer la formule ci-contre :
en remplaçant les éléments connus par leur valeur :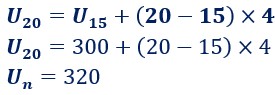
Calculons maintenant son premier terme Uo soit à partir de U15 soit à partir de U20 .
Voyons à partir de U15 :
il faut bien faire attention que le terme de niveau le plus haut soit dans le premier membre de la formule. Dans notre cas le terme cherché se trouve dans le second membre :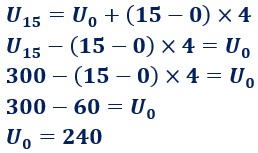
Et nous obtenons la suite :
Termes équidistants d’un autre terme.
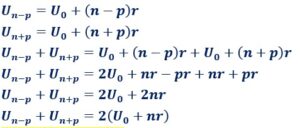
Soit la suite Un de premier terme 7 et de raison 5 représentée ci-dessous.
Les termes U1 et U7 sont tous les deux équidistants du terme U4 puisqu’ils sont séparés chacun de U4 par deux termes.
On voit bien que la somme de ces deux termes est égale à 2 fois le terme central. 
On peut faire la même expérience avec deux autres termes pourvu qu’ils soient symétriques par rapport à un troisième.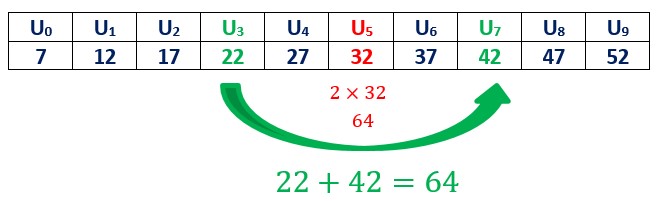 
Graphiques
Représentation sur une droite.
La suite :
est représenté graphiquement ci-dessous :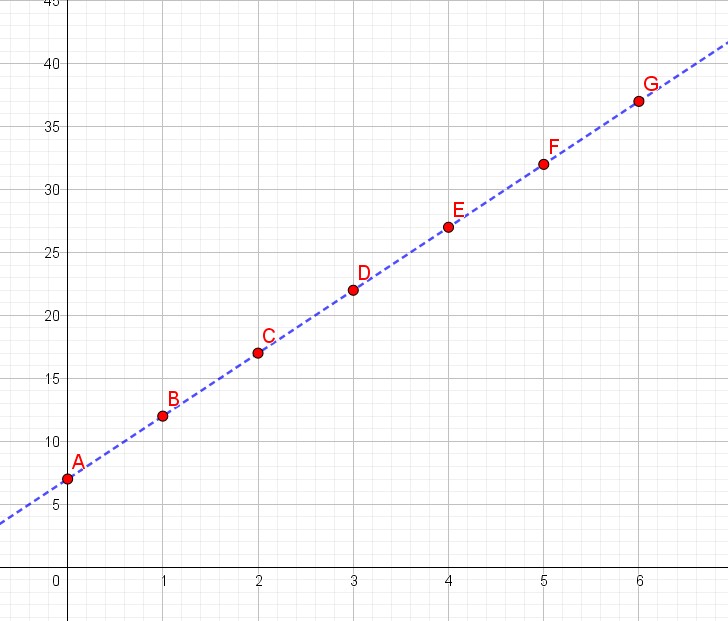
A chaque valeur de n ∈ Ν (ensemble des entiers naturels :0,1,2,3,……….) sur l’axe des abscisses correspond la valeur de Un sur l’axe des ordonnées. Tous ces points sont situés sur la droite d’équation 
. Mais la droite (tracée en pointillés) qui est continue ne représente pas graphiquement la suite. Seuls, les points tracés en rouge (A,B,C,….) représentent la suite car elle a des valeurs discrètes (discontinues). Sur le graphique, on voit bien que la suite est croissante.
Représentation sur une droite.
La suite :
est représenté graphiquement ci-dessous :
A chaque valeur de n ∈ Ν (ensemble des entiers naturels :0,1,2,3,……….) sur l’axe des abscisses correspond la valeur de Un sue l’axe des ordonnées. Tous ces points sont situés sur la droite d’équation 
. Mais la droite (tracée en pointillés) qui est continue ne représente pas graphiquement la suite. Seuls, les points tracés en rouge (A,B,C,….) représentent la suite car elle a des valeurs discrètes (discontinues). Sur le graphique, on voit bien que la suite est décroissante.
Représentation sur l’axe des abscisses lorsque la suite est définie par récurrence.
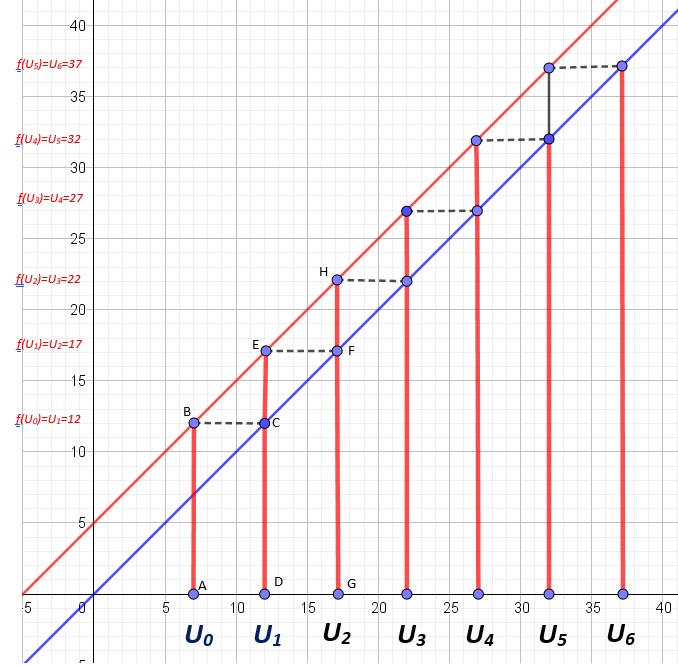On trace la droite d’équation .
On trace la droite d’équation y=x qui est la bissectrice du premier quadrant.
On place x0=7 sur l’axe des abscisses (Point A).
On mène la perpendiculaire à l’axe des abscisse à partir de ce point A. Elle coupe la droite rouge d’équation en B.
On obtient ainsi f(U0).
On mène une horizontale de B jusqu’à intercepter le droite d’équation y=x en C.
On projette ce point C sur l’axe des abscisses pour obtenir U1 au point D .
On recommence l’opération.
On obtient ainsi de proche en proche les valeurs de la suite U : U0,U1,U2…….
Représentation sur l’axe des abscisses lorsque la suite est définie par récurrence. 
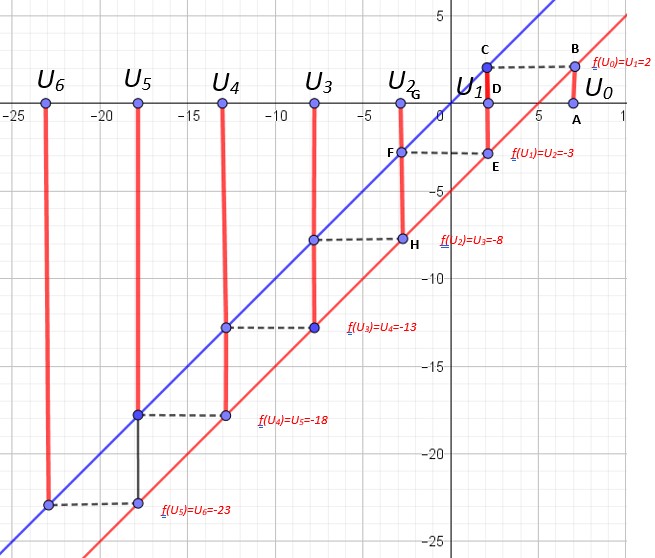
On trace la droite d’équation
On trace la droite d’équation y =x, bissectrice du premier quadrant.
On place x0=7 sur l’axe des abscisses (point A).
On mène la perpendiculaire à l’axe des abscisses à partir de ce point A.
Elle coupe la droite d’équation en B.
On obtient ainsi U0.
On mène une horizontale de B jusqu’à intercepter la droite d’équation y=x en C.
On projette ce point C sur l’axe des abscisses pour obtenir U1 au point D.
On recommence l’opération.
On obtient de proche en proche les valeurs de la suite U :
U0,U1,U2,….
C’est exactement le même processus que ci-contre, sauf que la droite rouge représentant la suite est maintenant en dessous de la droite y=x. il y a lieu de bien faire attention pour ne pas se tromper.
Somme des termes d'une suite arithmétique
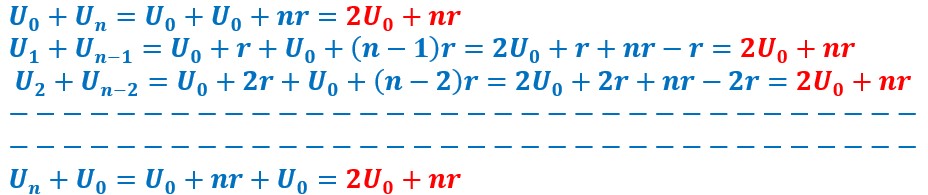
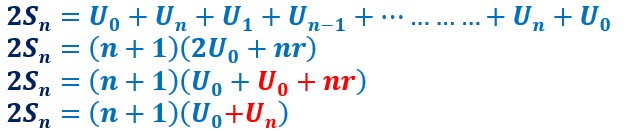
Soit la suiteUn.
On écrit la somme de ses termes de U0 à Un dans la première ligne et de Un à U0 dans la seconde ligne.
En additionnant les deux termes extrêmes U0 et Un, puis les deux termes équidistants des extrémités U1 eu Un-1 et ainsi de suite, on remarque que le résultat est toujours le même (en rouge). ce résultat résulte aussi de la propriété concernant les termes équidistants d’un autre terme.
On remarque que la somme comporte n+1 termes puisque le premier terme est U0.
On additionne les deux lignes du début en traduisant les termes en fonction de U0 et n. On a donc la somme de n+1 termes égaux.
On aboutit ainsi à la formule de la somme des termes de Uo à Un
la formule sera modifiée si on effectue la somme des termes de U1 à Un.
Enfin, on peut la généraliser explicitement en français.
Attention :
Le nombre de termes compris entre le rang p inclus et le rang n inclus est égal à la différence n-p plus 1 : n-p+1.
C’est un problème d’intervalles abordé autrefois en CM.