Racine carrée 4-3
Opération inverse de l'élévation au carré
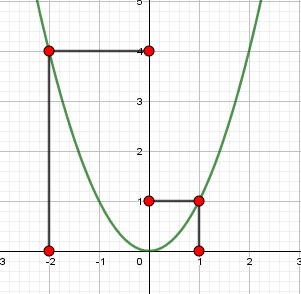
Elever un nombre au carré
Le carré de 4 est 16. le carré de -4 est 16.
Le carré de 6 est 36. Le carré de -6 est 36.
Le carré de a est a². Le carré de -a est a².
Tout nombre appartenant à l’ensemble des nombres réel possède un carré.Le carré d’un nombre négatif existe. 
Elever au carré est une fonction : 
A chaque nombre réel positif ou négatif correspond une et une seule image (c’est la définition d’une fonction).
Prendre la racine carrée d’un nombre.
La racine carrée de 16 est 4
La racine carré de 36 est 6
La racine carrée de a² est a
Seuls les nombres réels positifs possèdent une racine carrée. Il n’existe pas de racine carré d’un nombre négatif. 
De plus la racine carrée d’un nombre est toujours positive. 
En effet racine carrée est une fonction : 
.
A chaque nombre réel positif (puisqu’il n’existe pas de racine carrée d’un réel négatif) correspond une et une seule image .
est une autre fonction donnant une racine carrée négative.
Par contre nous verrons que 
C’est subtil ! Les mathématiques sont très formalisées et précises.
Définition
La racine carré de a positif est le nombre positif dont le carré est a
Racines carrées de carrés parfaits.
Racines carrées utiles à savoir car souvent utilisées.
Autrement dit, la racine carrée d’un nombre est un nombre positif qui, multiplié par lui même donne le nombre de départ.
Valeur exacte et valeur approchée :
La valeur exacte de racine de 2 est 
Une valeur approchée est 
suivant la précision demandée.
Racine carrée d’un carré :
Les deux opérations “élever au carré” et “prendre la racine carrée” étant deux opérations inverses, il est évident que :
Opérations sur les racines carrées
Somme de deux racines carrées
la somme des racines carrées de deux nombres est différente de la racine carrée de la somme des deux nombres.
si les deux nombres sont identiques :
Différence de deux racines carrées :
La différence entre deux racines carrées de deux nombres est différente de la racine carrée de la différence des deux nombres. 
SI les deux nombres sont identiques :
Produit de deux racines carrées :
Le produit des racines carrées de deux nombres est égal à la racine carrée du produit des deux nombres et inversement :
Quotient de deux racines carrées :
Le quotient des racines carrées de deux nombres est égal à la racine carrée des quotients des deux nombres et inversement à condition que le dénominateur soit différent de 0 :
Carré d’une racine carrée
Le carré d’une racine carré est le nombre lui-même 
Somme de deux racines carrées :
Différence entre deux racines :
Produit de deux racines carrées :
Quotient de deux racines carrées :
Carré d’une racine carrée :
Extraire un carré d'une racine carrée
Il est intéressant d’extraire un carré parfait d’une racine carré afin de simplifier les calculs.
Pour éviter de faire la décomposition de la première ligne, on peut se dire mentalement “j’ai un carré parfait a², j’extrait, je sorts ce carré parfait de dessous le radical pour le placer à gauche de ce radical. En sortant a² de dessous le radical, il devient sa racine carrée qui est a”
Exemples :
Je cherche dans la table de multiplication un nombre qui soit à la fois un carré et un diviseur de 72. Miracle ! 9 répond à nos exigences. Au lieu d’écrire 72, j’écris 9×8. Je décompose les radicaux selon la propriété de la multiplication des racines. Je sais que la racine de 9 est 3.
Je peux aussi dire que sous le radical, j’ai un 9 qui est un carré parfait, je l’extrais du radical en prenant sa racine carrée 3. Ainsi je passe directement au résultat sans passer par la décomposition des racines. 
Rendre rationnel le dénominateur d'une fraction
Parfois on a des fractions qui possèdent des radicaux au dénominateur. C’est difficile à manier dans les calculs et on a intérêt à rendre le dénominateur rationnel, c’est-à-dire faire en sorte qu’il n’y ait pas de radicaux au dénominateur.
Premier cas, un seul radical au dénominateur :
Nous savons qu’on peut multiplier ou diviser le numérateur et le dénominateur d’une fraction par un même nombre sans changer la valeur de la fraction.
Il nous suffit donc de multiplier les deux termes de la fraction par 
pour qu’au dénominateur le radical soit éliminé.
Deuxième cas, somme ou différence de deux racines :
Revenons à la troisième identité remarquable 
(a+b) est la quantité conjuguée de (a-b) et inversement.
Lorsqu’on multiplie les deux quantités conjuguée on obtient la différence de deux carrés. On peut donc éliminer les radicaux de cette façon.
Au dénominateur de la fraction nous avons la différence de deux racines : 
. La quantité conjuguée de cette expression est 
. On multiplie le numérateur et le dénominateur de cette fraction par cette quantité conjuguée. Grâce à la troisième identité remarquable, les deux radicaux disparaissent.
Le principe est identique sauf qu’au dénominateur on a l’expression dont la quantité conjuguée est .
Un seul radical au dénominateur :
Il faut éliminer le 
du dénominateur.
Pour cela, on multiplie le dénominateur et le numérateur de la fraction par . Le reste des calculs en découle.
Somme ou différence de deux racines au dénominateur.
Au dénominateur nous avons 
au dénominateur . Il nous faut multiplier le numérateur et le dénominateur par la quantité conjuguée, 
pour éliminer les radicaux au dénominateur.
Ensuite les calculs sont tout à fait classiques. IL faut considérer la racine d’un nombre avec son radical comme un nombre, car c’est un nombre.
Cette fois nous avons 
au dénominateur.Il ne faut pas se laisser troubler par le fait qu’il n’y a qu’un seul radical. Cette quantité possède bien une quantité conjuguée qui sera 
. Il ne rest plus qu’à faire les calculs classiques pour trouver le résultat.
Somme et différence de plusieurs racines carrées
Principe :
comme on ne peut pas additionner ou soustraire des poires et des pommes, on ne peut pas additionner ou soustraire des 
et des 
ou des 
avec des 
.
Mais on peut additionner ou soustraire des avec des ou des avec des .
En résumé, on ne peut additionner ou soustraire que des objets mathématiques ou non qui portent exactement le même nom.
Dans cette exemple toutes les racines sont des , on peut donc les additionner sans crainte.
Dans celui-ci on a des et des .
On additionne ensemble les puis ensemble les .
On ne peut rien calculer dans les parenthèses. On les supprime en faisant attention au signe moins devant la deuxième parenthèse.
On regroupe les termes qui ont le même nom. On les additionne.
Racines carrées et développement
On utilise les mêmes règles de calculs apprises pour l’ensemble des réels car les racines carrées sont des nombres réels, avec en plus, compte tenu de l’écriture avec des radicaux, les règles énoncées ci-dessus.
Simple distributivité :
Double distributivité : 
Attention ! Je pense qu’il est préférable d’écrire 
plutôt que 
pour éviter la confusion avec 
.En écriture manuscrite on peut prolonger le signe du radical par inadvertance jusqu’au dessus du a, ce qui serait faut. Avec la première écriture préconisée il n’y a aucune confusion possible.
Une réponse
si en étant gamin j’avais eu internet ….. j’aurais épargné bien des heures d’étude !!!
bellles explications !