Le courant alternatif sinusoïdal
- par gabriel
- dans Electricité, Physique
- sur 18 février 2022
Comment ça marche !

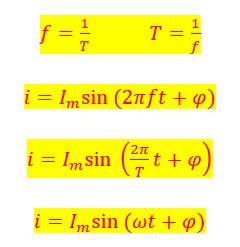
Sur l’animation ci-contre, réglons le curseur i sur la position i=1.
Les électrons rouges présents dans les fils conducteurs se mettent en mouvement et la lampe s’allume. Au bout d’un instant, on s’aperçoit que les électrons changent de sens. Après un autre instant, ils reprennent leur course initiale pour changer ensuite de sens. Cela se produit indéfiniment. On peut observer ces changements de sens alternatifs des électrons sur le curseur rouge placé sous le générateur.
Pour i=1 on note que les électrons font un aller et retour en environ 20 s. Environ , car les mesures faites ainsi ne peuvent pas être très précises et dépendent de nombreux facteurs. On dit que la période du courant est T=20 s
Pour i=2 on note un aller et retour en 10 s. Donc T= 10 s
Pour i=3 on note un aller et retour en 6 s. T=6 s
Pour i=4 on note un aller et retour en 5 s. T=5 s
Pour i=5 on note un aller et retour en 4 s. T=4 s
Notons que la lampe brille de plus en plus entre i=1 et i=5.
Pour i=1 si les électrons mettent 20 s pour effectuer un aller et retour, on peut dire aussi qu’ils font un vingtième d’aller et retour en 1 s. Soit 1/20
Ce nombre d’aller et retour en une seconde est appelé la fréquence f ou ν (nu). Son unité est le Hertz (Hz)
Pour i=2 ;3 ; 4 ou 5 la fréquence serait respectivement de 1/10 ; 1/6 ; 1/5 ; 1/4 de Hertz. A notre échelle d’animation on ne peut obtenir que des fractions de Hertz, des fractions d’aller et retour. Pour i=1 les électrons ne parcourent que le vingtième d’un aller et retour en une seconde.
Notre courant électrique domestique en France, celui que nous captons sur les prises de nos maisons, vibre à raison de 50 hertz, c’est-à-dire 50 aller et retour en une seconde !
Nous voyons que l’intensité i du courant , correspondant à l’éclat, la brillance de la lampe, est en relation avec la période donc avec la fréquence de ce courant. Mais cette intensité varie au rythme des alternances pour atteindre à chacune d’elle une valeur maximum Im.
Ainsi l’intensité i varie-t-elle en fonction du temps t. C’est l’intensité instantanée. Elle est donnée par l’une des trois équation ci-contre.
Dans la première, l’intensité instantanée i est donnée en fonction de la fréquence f.
Dans la deuxième, elle est donnée en fonction de la période T.
Dans la troisième elle est donnée en fonction de ce qu’on appelle la pulsation ω.
Mais qu’est-ce donc cette pulsation ω.
D’où ces 2π viennent-ils ?
Intensité maximale
Comportement d’un électron suivant l’intensité maximale
régler le curseur sur a=0.5 et cliquer sur démarrer
Pour une même fréquence (pour le même nombre d’aller et retour en une seconde) donc pour une même période ( temps mis pour un aller et retour), nous montrons avec l’animation ci contre le parcours de 4 électrons dans 4 circuits différents suivant l’intensité maximale Im.
admettons que les intensités représentées soient en mili Ampères, mA.
Dans le premier cas l’intensité maximale est de 0,5 mA, l’électron parcoure un chemin représenté par le segment vert en un temps t.
Dans le deuxième cas elle est de 1 mA, l’électron parcoure le double de chemin dans le même temps t.
Dans le troisième cas elle est de 2 mA et l’électron parcoure 4 fois plus de chemin que le premier dans le même temps t.
Enfin, dans le quatrième cas l’intensité maximale est de 3 mA et l’électron parcoure 6 fois plus de chemin que le premier dans le même temps t.
Explication de l' expression de l'intensité instantanée
Je clique sur la petite flèche en bas à gauche jusqu’à ce que le point A prenne une position entre O et A1; Je clique à nouveau pour arrêter le mouvement. A ce moment je suis à un instant t.
Je lis le texte ci-contre.
Dans l’animation ci-contre le point A représente un électron qui se déplace alternativement entre A1 et A2.
L’intensité est représentée par le segment OA.
On voit que OA varie.
A est la projection du point B sur l’axe A1A2.
B se déplace sur le cercle de centre O et de rayon OA1.
B se déplace sur ce cercle à vitesse constante.
OA est le sinus de l’angle BOΩ.
Pendant que le point A (notre électron) effectue un aller et retour entre A1 et A2, le point B décrit le cercle complet soit un angle de 360° ou 2π radians.
Si B effectue 2 tours 2 fois 2π radians , A fait 2 allers et retours, 2 Hertz.
Si B fait f tours, soit f fois 2π, A effectue f allers et retour et OA correspondant à l’intensité i à ce moment a donc pour valeur sin(2πf ).
Comme f=1/T i a aussi pour valeur sin(2π/T).
Mais 2πf correspond à l’arc parcouru par le point B sur le cercle. Cet arc de cercle c’est ω. Donc i est aussi égal à sin(ω)
Tout cela à un moment t donné.
Il nous reste à expliquer φ et Im.


Si nous déclenchons le chronomètre et l’animation en même temps alors que le point A, l’électron est en O à l’origine et le point B en Ω à l’origine des angles, OA=0 et l’angle BAΩ =0.
Tous les paramètres sont nuls lorsqu’on déclenche le chronomètre et l’animation simultanément.
Dans ce cas l’équation donnant l’intensité instantanée i en fonction du temps t est tout simplement ;
i=sin(2πft) ou i=sin(2π/T.t) ou encore i=sin(ωt).


Cette fois, nous déclenchons le chronomètre lorsque le point A a déjà parcouru une certaine distance, ici OA=0,5
Dans ce cas l’angle BOA est égal à 0,52 radians soit (π/3) radians.
Pour connaître l’intensité instantanée i à un moment donné après le déclanchement du chronomètre, il nous faut ajouter la distance OA parcourue avant correspondant au balayement par B de l’angle 0,52 radians.
Ainsi cette intensité instantanée i sera :
i=sin(2πft+0.52) ou i=sin(2π/T.t+π/3) ou i=sin(ωt+π/3)
Ainsi le nombre φ, ici 0,52 ou π/3 représente le décalage de la position de A après le déclenchement du chronomètre, par rapport à l’origine des temps t .
φ est la phase à l’origine.
Dans l’animation ci-dessus, un électron E parcours une partie d’un circuit CD.
La distance maximum par rapport à l’origine O de l’électron E est atteinte pour OE=OC. C’est l’intensité maximale Im. Ici Im =3.
La courbe sinusoïdale bleue matérialise la distance du point A à partir de l’origine O donc de l’électron E en fonction du temps t.
A parcours cette courbe, alors que E parcours le segment CD comme si on avait étiré le facteur temps représenté sur l’axe des abscisses.
Nous remarquons que sur notre graphique, la période est de 6,28 s, soit une fréquence de 0,16 hertz et donc une pulsation de 0,16x2x3,14≅1 rad par s et une intensité maximale de 3 A.
L’équation donnant l’intensité instantanée i en fonction du temps t sera :

Soit un électron E comme sur l’animation précédente.
Soit un électron G qui parcoure la même portion de circuit entre C et D, à la même fréquence que l’électron E.
Mais il est en avance sur E. Son avance représentée par le segment EG est constante.
Ce segment EG correspond à une valeur de sinus d’un angle.
Si on arrête l’animation de telle façon que l’électron E soit à l’origine O, on voit que l’électron G est situé à une distance de 1,5. Cette distance est multipliée par 3 du fait de l’intensité maximale Im=3. Son avance est en fait égale à un sinus dont la valeur est 0,5 et dont l’angle correspondant est égal à π/3.
On appelle ce décalage phase à l’origine symbolisée par le nombre φ.
La phase à l’origine de l’électron E est φ=0 d’où les équations de l’intensité ci-dessus.
La phase à l’origine de l’électron G est φ= π/3 ≅1,05 radians. Et les équations de l’intensité de l’électron G sont :