Repère, points, vecteurs droites dans le plan
Repère
Pour trouver quelqu’un on a besoin de son adresse. On le repère grâce à son adresse.
Pour sauver les passager d’un bateau en détresse, on a besoin de le repérer grâce à sa latitude et sa longitude.
Dans un plan, on a souvent besoin de le positionner, de le repérer. Comme dans un plan, il existe deux dimensions (gauche/droite et avant/arrière) on aura besoin de deux axes quelconques.
Sur la figure ci-contre, on a tracé un axe bleu “horizontal” et un axe rouge qui coupe l’axe bleu en un point O.
On n’est absolument pas obligé de tracer l’axe bleu horizontal. On peut le tracer n’importe comment. L’important est qu’on décide ce qu’il sera.
L’axe bleu ou x’Ox se nomme axe des abscisses.
L’axe rouge ou y’Oy se nomme axe des ordonnées.
Sur l’axe des abscisses on trace un vecteur i représentant l’unité de l’axe.
Sur l’axe des ordonnées on trace un vecteur j représentant son unité.
Soit un point A du plan.
On projette ce point A sur l’axe des abscisse selon la direction données par l’axe des ordonnées. On obtient un point A’
On projette le point A sur l’axe des ordonnées suivant la direction donnée par l’axe des abscisses. On obtient le point A”.
OA’ 4 fois le vecteur i OA” vaut 3 fois le vecteur j
Ces chiffres 4 et 3 sont les coordonnées du point A qui permettent de le repérer très précisément dans le plan.
Pour repérer un point, on commence toujours par son abscisse puis son ordonnée selon la syntaxe (manière d’écrire) suivante :
Nom du point /parenthèse /son abscisse /point virgule /son ordonnée/ parenthèse
Vecteurs
Sauf mention contraire toutes les formules indiquées sont valables quel que soit le repère utilisé. Pour des raisons pratiques nous utilisons des repères orthonormés.
Coordonnées d’un vecteur.
Représentant d’un vecteur :
Produit d’un vecteur par un scalaire. 
Somme de deux vecteurs.
Déterminant de deux vecteurs.
Vecteurs colinéaires
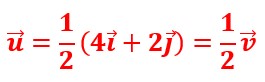
Norme d’un vecteur. (valable uniquement dans un repère orthonormé)
Puisque le repère est orthonormé, le triangle ABC est rectangle en C.
On peut donc utiliser le théorème de Pythagore. 
Dans le cas particulier :
Coordonnées du milieu d’un segment. 
Produit scalaire. Vecteurs orthogonaux.
La droite
Equations paramétriques d’une droite.
Ce sont les deux équations paramétriques de la droit (d) de paramètre k.
Soit le point A appartenant à la droite (d). Soit un point M quelconque de la droite (d).
Soit un vecteur u parallèle à la droite (d).Ce vecteur donne la direction de la droite, on le nomme vecteur directeur de la droite.
Les vecteurs AM et u sont colinéaires
Nous en déduisons :
Ainsi, selon les valeurs du paramètre k dans l’ensemble des réels, on détermine grâce à ces deux équations paramétriques une infinité de points appartenant à la droite (d).
Ci-dessous on a déterminé 3 points P,P’ et P” de la droite non inscrits dans le graphique mais qui peuvent être facilement repérés. 
Equation cartésienne d’une droite. Première méthode
A partir des deux équations paramétriques, on calcule k dans la première équation par exemple. 
On reporte cette valeur de k dans la seconde équation paramétrique. Puis on calcule. 
On aboutit à une équation de la forme :
Cette équation à deux inconnues représentant l’abscisse et l’ordonnée des points de la droite est appelée équation cartésienne en mémoire de René Descartes.
Il n’est pas question de retenir par coeur la formule donnant l’équation cartésienne à partir des équations paramétriques.
Il suffit de conduire les calculs à partir des équations paramétriques.
Pour l’exemple ci contre nous avions trouvé les deux équations paramétriques.
Calculons la valeur de k en fonction de x et y dans la première équation. 
Reportons cette valeur de k dans la seconde équation. 
Il suffit maintenant de continuer les calculs. 
On obtient une équation dont on peut multiplier les deux membres par -1.
Ainsi obtient-on l’équation cartésienne de la droite (d)
Cette équation signifie :
Tous les points de la droite (d) sont tels que deux fois leur abscisse moins trois fois leur ordonnée plus 6 est égal à 0.
On a choisi, bien sûr d’écrire l’équation la plus simple.
Mais on aurait pu choisir cette équation :
Equation cartésienne d’une droite. Deuxième méthode.
On obtient une équation de la forme
Là aussi, pas question de connaître la formule par coeur.
On effectue des calculs à partir du déterminant de deux vecteurs. 
Les deux vecteurs sont colinéaires, leur déterminant est nul.
On trouve très facilement l’équation cartésienne.