Statistiques à deux variables
Un exemple
Soit les deux séries statistiques suivantes :
La première série en rouge donne l’âge de 6 personnes. Sa variable est X et les différents âges xi.
x1=36, x2=42, ….x6=66
La seconde série en bleu donne les tensions respectives de chacune de ces 6 personnes. Sa variable est Y et les différentes tensions yi.
y1=12, y2=13,5 …… y6=15
Le but final sera de savoir s’il existe une corrélation entre l’âge des personnes et leur tension. Autrement dit, savoir si l’âge de la personne influence sa tension.
Droite d'ajustement passsant par le point moyen
Construction de la droite de régression de deux séries statistiques.
Nous verrons plus loin à quoi peut bien servir cette droite de régression.
Mais pour la construire ici nous avons utilisé notre pifomètre, ce qui n’est pas très précis.
Nous pouvons augmenter la précision en utilisant deux points moyen.,
Nous verrons ensuite une autre méthode beaucoup plus précise et mathématique la méthode des moindre carrés.
Pour cela nous allons représenter les deux séries dans un graphique.
En abscisse les valeurs de la série X
Sur l’axe nous prendrons des valeurs allant de 35 à 75.
En ordonnée les valeurs de la série Y .
Sur l’axe nous prendrons des valeurs allant de 11,5 à 16,5
Ainsi le premier point appelé A aura pour abscisse la valeur x1 et pour ordonnée la valeur y1.
Pour construire tous les points glisser le curseur n vers la droite.
1 rien ne se passe
2 rien ne se passe
3 Abscisse du point A =36
4 Ordonnée du point A = 12
5 Construction du point A(36;12)
6 COnstruction du point B(42;13.5)
7 à 10 COnstructions des point C,D,E,F
La moyenne des âges xi est égale à 
La moyenne des tensions yi est égale à 
Construisons le point G appelé point moyen dont les coordonnées sont respectivement la moyenne des X, la moyenne des Y
11 Construction du point G
Nous voyons que les points A,B,C,D,E,F sont situés de part et d’autre d’une droite imaginaire passant par G. Cette droite doit passer au plus près de chacun des points. Nous la construisons dans ce cas au pifomètre. Elle est appelée droite de régression.
12 Construction de la droite de régression.
On voit que cette droite coupe l’axe des ordonnées au point de coordonnées 0,12 Appelons ce point U
13 Construction du point U
Pour calculer l’équation de cette droite notons sur le graphique les accroissements respectifs des X et des Y entre les point U et G
14 Constructions des accroissements entre U et G.
Le coefficient diresteur a de la droite est égal au taux d’accroissement τ sachant que U(35;12) et G(51;13,8) et que l’équation d’une droite est de la forme y=ax+b.
On sait que b=12. D’où l’équation de la droite
Droite d'ajustement passsant par deux points moyens
Reprenons les deux mêmes suites statistiques.
Calculons le point moyen G1 des trois premiers points A,B,C.
La moyenne des trois premiers xi est :
La moyenne des trois premiers yi est :
Les coordonnées du point G1 seront donc ; 
Construisons le dans le graphique ci-contre
n=2 Construction du point G1
Calculons le point moyen des trois derniers points D,F,G.
n=3 Construction du point G2
En joingnant les deux poins G1 et G2 on obtient la droite de régression.
n=4 Construction de la droite de régression.
Cette droite coupe l’axe des ordonnées en un point U.
n=5 Construction du point U avec estimation de ses coordonnées. SOn ordonnée est 11,84.
n=6 Construction des accroissement des xi et yi.
La droite est de la forme y=ax+b.
On sait que b=11,84
Calculons le coefficient directeur a de cette droite. Il est égal au taux d’accroissement entre les points G1 et G2.
Droite d'ajustement par la méthode des moindre carrés
En partant de cette expressin nous allons démontrer les deux formules donnant le coefficient directeur de la droite de régression a et son ordonnée à l’origine b.
Mais avant cette démonstration, calculons l’équation de la droite de régession de notre exemple tension selon l’âge avec ces deux formules.
la courbe de régression linéaire est comme son nom l’indique (linéaire= ligne) une droite qui va passer au plus près de chacun des points du nuage.
Suposons que nous connaissions cette droite et donc son équation qui sera de la forme y= ax+b et traçons la dans le graphique ci-contre.
n=1 nuage des points appelés M
n=2 construction de la droite d’ajustement ou aussi appelée droite de régression.
n=3 projetons chacun des points du nuage sur la droite de régression parallèlement à l’axe des ordonnées.
n=4 constrruisons chaque distance du point du nuage à son projeté sur la droite.
n=5 l’ordonnée de chaque point du nuage est donnée dans le tableau
n=6 tout point de la droite de régression vérifie l’équation de cette droite. L’ordonnée de chaque point de la droite est égale à a fois son abscisse plus b; Ce qui est bien sûr vrai pour tous les projetés M’
n=7 Nous en déduisons la valeur de chaque distance entre un point du nuage est son projeté sur la droite;
n=8 on prend le carré de chacune des distance pour écviter les nombrs négatifs. .
n=9 Comme la droite d’ajustement ou de régression doit passer au plus près d’un des points, cela signifie que la distance d doit être minimume. Mais elle doit passer au plus près de chacun des points, donc la somme des distances devra être minimume.
Il s’agit maintenant de déterminer les valeurs a et b pour avoir l’équation de la droite de régression.
Mais généralisons et au lieu d’avoir 6 points prenons un nombre n de points.
Calcul de l'équation de la droite avec la méthode des moindre carrés
Formule de la covariance et formule de la variance :
Pour la variance des xi nous avons besoin d’élever chacun des xi au carré. C’est ce que nous faisons dans la ligne âge²
Pour la covarience des xiyi, nous avons besoin du produit de l’âge avec la tension, le produit xiyi. Ce qui est fait dans la ligne Age x tension.
Covariance(x,y)
La somme des xiyi est donnée dans la colonne somme et est égale à 4290.Cette somme doit être divisée par 6 : 715
La moyenne des âges xi est égale à 51
La moyenne des tensions yi est égale à 13.8
Leur produit est égal 703,8.
La convarience( x,y ) sera donc : 715-51 x 13.8 =11.2
Varience de xi
La somme des xi² est égale à 16236. Cette somme des xi² divisée par 6 est égale à 2706
La moyenne des xi est égale à 51 élevée au carré : 2601
Ainsi la varience sera égale à 2706-2601=105
Coefficient directeur de la droite de régression a
Il est égal à la covarience des xi,yi divisée par la varience de xi
Soit 11.2 : 105 = 0, 1066666 que l’on peut arrondir à 0,107.
Accrochez vous : démonstration
Nous partons comme indiqué plus haut de la formule donnant la somme des écarts entre chacun des points et la droite de régression supposée connue dont les paramètres sont le coefficient directeur a etson ordonnée à l’origine b. 
Désignons pour simplifier les écritures par S cette somme des écarts. 
Calculons entre les crochets
Dérivons le second membre par rapport à la variable a 
Factorisons le -1 de -xi
Distribuons le xi de la parenthèse dans le crochet 
Pour trouver le minimum ou le maximum d’une dérivée , il suffit qu’elle soit nulle. 
Pour qu’un produit de facteurs soit nul il faut et il suffit qu’un des facteurs soit nul.
La sommation d’une somme est égale à la somme des sommations de chaque terme
Divisons les deux membres par n. Il est évident que 0/n=0
Pour le dernier terme de cette somme, nous avons b fois le somme des xi divisée par n. Il s’agit de b fois la moyenne des xi notée x barre.
Isolons le premier terme dans le epremier membre et les deux autres termes dans le second. 
Quelques rappels ou précisions de calculs.
Nous utilisons les dérivées partielles.
Dans la formule ci contre nous avons deux inconnues, deux variables a et b qui représentent toutes les possibilités de droite possible. Tous les autres termes sont des nombres connus.
Dériver par rapport à a c’est aussi considérer la valeur b comme étant fixe, déterminée.
Nous devons donc dériver 
C’est une fonction composée. A partir de la variable a on calcul l’expression entre crochet puis on élève au carré. Nous savons que la dérive d’une telle fonction est égale à 2UU’, U’ étant la dérivée de l’expression entre crochet dont la variable et rappelons le a et tous les autres termes des nombres connus. La dérivée de l’expression entre crocher sera donc : -xi.
Cela peut paraître difficile. Mais il suffit de faire abstraction du fait de considérer x comme variable. Dans ce cas c’est a qui est la variable et uniquement a. Les autres termes sont des nombres bien déterminés même b à ce stade.
Les propriétés des sommations.
Les nombres possédant un indice prennet différentes valeurs selon leur indice. Dans le tableau donné pour i=1 on a x1=36 …..
Les nombres n’ayant pas d’indice ne changent pas. Ils sont fixes.
Aussi nous pouvons appliquer la règle suivante résumant deux règles fondamentales. 
Nous avons précédemment dérivé l’expression ci-dessus par rapport à la variable a. Dérivons la maintenant par rapport à la variable b.
On sait que la dérivée de -x est -1. Notre variable n’est pas x mais b. Nous avons -b, sa dérivée sera donc -. On a encore ici une fonction composée.
-1 X 2 =-2 que nous plaçons devant le crochet. 
On peut même le placer devant le signe de sommation.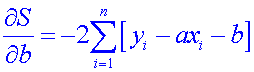
Pour que l’expression de départ soit minimume il faut que sa dérivée soit nulle.
Il suffit que le second facteur soit nul. 
On distribue les signes de sommation. 
La somme de b pour des itérations allant de 1 à n est évidemment égale à n fois b =nb
On isole les yi dans le premier membre et toutes les autres expressions dans le second. 
On divise les deux membres par n. 
On obtient une équation telle que la moyenne des y est égale à a fois la moyenne des x plus b.
Cette équation traduit le fait qu’un point dont son abscisse est égale à la moyenne des x et son ordonnée est égale à la moyenne des y vérifie l’équation ci-dessus. Ce point est le point G
Ainsi nous obtenons un système de deux équations à deux inconnues a et b. Nous savons parfaitement résoudre ce genre de système. Il ne faut pas se laisser impressionner par la complexité de chacun des termes.
Calculons la valeur de b en fonction de la valeur de a dans la première équation. On repporte cete valeur dans la seconde équation. 
Toujours dans cette seconde équation, on distribue 
Toujous dans la seconde équation, on distribue. On isole dans l epemier membre tous les termes qui contiennent les valeurs y 
Oh surprise : le premier membre corespond à la covarience entre x et y alors que le second membre correspond à la variance des x.
Nous en déduisons la valeur de a, le coefficient directeur de la droite de régression cherchée. Et, connaissant a, nous pouvons calculer b dans la première équation du systême. 
Résumlé de la démonstration :
A partir de la formule cfi-dessus :
On calcule les deux dérivées partielles :
Dérivée par apport à a.
Dérivée par rapport à b.
L’expression rouge sera minimume si les deux dérivées sont nules.
On pose donc :
dérivée par rapport à a =0
dérivée par rapport à b =0
On obtient un système de deux équations à deux inconnues a et b
En le résolvant on trouve la valeur de a et de b et donc l’équation de la droite de régression.
rappelons que cette droite de régression est l’unique droite qui passe au plus près de chacun des points de coordonnées (xi,yi)
Coefficient de corrélation linéaire
Le coefficient de corrélation linéaire détermine si le nuage de points est plus ou moins aligné et donc si la deuxième série en y est plus ou moins influencée par la première série des x.
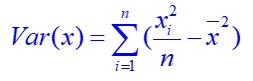
Si r est proche de 1, la seconde série est fortement influencée positivement par la première. Quand les x croissent les y croissent. On dit qu’il y a une corrélation positive.
Si r est proche de -1, la seconde série est fortement influencée négativement par la première. Lorsque les x croissent les y décroissent. On dit qu’il y a une corrélation négative.
Si r est proche de 0, la seconde série n’est pas influencée par la première. Il n’y a pas de corrélation entre les deux.
Corrélation positive parfaite
Corrélation négative parfaite
Pour r >0,8 ou r < -0,8 on a une bonne corrélation
r est très proche de 0. On n’a aucune corrélation.
Maintenant on voudrait savoir si nos deux séries statistiques sont plus ou moins fortement liées. C’est à dire, dans notre exemple concret si l’âge de la personne influence sa tension. Autrement dit savoir si plus on est vieux, plus la tension est forte ou bien plus on est vieux moins la tension est forte. A moins qu’il n’y ait aucun rapport entre l’âge et la tension.
Il nous faut donc trouver un outil permettant une telle interprétation.
Nous savons que la covarience entre l’âge et la tension est la moyenne des distences entre chacune des valeurs et la droite.
Nous savons aussi que la varience des âges est le carré de la moyenne de l’écart à la moyenne des âges.
De même la varience des tensions est le carré de la moyenne des écarts à la moyenne des tensions.
Si la covarience entre l’âge et la tension est égale à la varience des âges multiplié par la varience des tensions, on poura dire que les tensions progressent en même temps que l’âge.
Par contre, si les duex valeurs sont très différentes, on pora dire qu’il n’y a aucune relation entre les âges et les tensions.
On va calculer le coefficient de corrélation linéaire r qui est égale à la covarience entre l’âge et la tension divisé par le produit des varience de l’âge et de la tension.
Calculons le coefficient de corrélation de notre exemple.
Ci-dessous le tableau dans lequel on n’a laissé que les résultats (moyenne, varience)
Dans le tableau, nous lisons les résultats suivants : 
Il nous rets à appliquer la formule :
Comme r est supérieur à 0,8 il existe une bonne corrélation entre les deux séries, entre cles âges et les tensions.
Nous pouvons affirmer que, en règle générale, la tension artérielle augmente avec l’âge.