Effet Doppler
- par gabriel
- dans Articles nouveaux, phénomènes périodiques, Physique
- sur 3 février 2024
Ajoutez votre titre ici
Ce qu'il faut savoir : révisions
Le son émis par la voix est une vibration des cordes vocales, transmise à l’air, puis au tympan de celui qui écoute.
Si je chante la note la, mes cordes vocales vont vibrer à raison de 440 aller et retour par seconde.
Ce nombre d’aller et retour en une seconde est appelé la fréquence.
Plus la note est haute et plus le nombre d’aller et retour est important.
On peut écouter des sons allant de 20 aller et retour par seconde à 20 000 aller et retour par seconde.
On appelle Hertz, ce nombre d’aller et retour par seconde, c’est l’unité de fréquence.
La période est le temps mis pour faire un aller et retour. Elle se mesure en seconde mais elle est d’ordre de la milliseconde.
On peut modéliser la vibration du son par une sinusoïde.
Ci-contre l’axe horizontal des abscisses est gradué en secondes. Il représente le temps qui s’écoule.
Sont représentés 3 sons de diverses fréquences et périoodes.
La période en secondes est égale à l’inverse de la fréquence en Hertz.
La fréquence en Hertz est égale à l’inverse de la période en secondes. 

Formule donnant la longueur d’onde en foction de la vitesse de l’onde en mètre par seconde et de la période en seconde ou de la fréquence en Hertz.
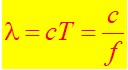
Ci-contre les formules indispensables pour ce chapitre.
Attention : la longueur d’onde est une distance exprimée en mètres. Elle ne peut pas être représentée sur le graphique puisque nous avons en abscisse du temps en secondes alors qu’il nous faudrait des distances en mètres.
Pour la représenter il faudrait élaborer un autre graphique.
On peut dire que la longueur d’onde est la distance séparant deux crêtes.
Sur une marre les cercles concentriques générés lorsqu’on lance un cailloux sont séparés par la longueur d’onde. De même à la surface de la mer, les vagues sont séparées par leur longueur d’onde. Mais on ne paut pas par contre visualiser leur période ou leur fréquence, pour cela il fuadrait le faire avec un chronomètre.
Effet Doppler avec le son
Ce qu'on entend
Ce qu'on voit et ce qu'on entend
tout le monde a vécu cette expérience presque quotidienne dans les grandes villes. Une voiture de pompier, une ambulence, une voiture de police ou de gendarmerie signale son passage par une sirène afin d’avertir les automobiliste qu’ils doivent la laisser passer. Lorsqu’on est sur le trottoire et que la voiture en question passe devant nous, nous entendons un son relativement aigu avant son passage et après son passage un son relativement plus grave. Pour te remémorer ce phénomène clique sur le bouton démarrer de l’animation ci-dessus.
Explication
Voiture immobile
Ciquer sur le bouton bleu »initialisation, puis sur le bouton bleu « Voiture immobile »
Pour arrêter momentanément l’animation et la reprendre cliquer sur le petit logo apparaissant en bas à gauche.
Les cercles représentent les crètes des ondes émises par la voiture ou dans le cas du son le maximum de compression d’une lamelle d’air lorsqu’elle vibre, le minimum de compression étant au milieu de deux crètes.
Le nombre de crètes par seconde représente la fréquence. Bien sûr, on ne peut pas représenter la réalité, on est obligé de modifier les données.
Lorsque la voiture est immobile, on voit bien que la distance entre deux crètes est constante.
Ainsi on écoute un son ayant toujours la même fréquence
Voiture en mouvement
Cliquer sur le bouton bleu « initialisation » puis deux fois sur le bouton bleu « Voiture en mouvement »
Pour arrêter momentanément l’animation et la reprendre cliquer sur le petit logo apparaissant en bas à gauche.
Lorsque lea voiture se déplace, la source sonore aussi puisque la sirène fait partie de la voiture.
Ainsi la source engendre des cercles ( les crètes de la vibration) à différents endroits.
Si on est avant la voiture, les crètes sont nettement plus proches. Cela correspond à une fréquence plus grande et donc à un son plus aigu.
Si on est après la voiture, les crètes sont plus éloignées les unes des autres. Cela correspond à une fréquence plus petite et donc un son plus grave.
Représentation des ondes avec Audacity
Le son entendu par l’observateur (bonhomme vert ) est représenté graphiquement ci-dessous.
En abscisse le temps et en ordonnée « l’intensité du son ». La fréquence (la hauteur du son grave ou aigu) est invisible sur ce graphique. Elle est représentée par des motifs plus ou moins serrés sur l’axe des abscisses.
Le son est pris en stéréophonie, avec deux microphones. En haut c’est la captation du micro de gauche et en bas la captation du micro de droite
Il existe un décalage temporel normal entre les deux graphiques puisque le micro de gauche capte le son avant le micro de droite. ce décalage n’existe pratiquement plus au centre du graphique lorsque la voiture passe devant l’observateur, donc devant les deux micros.

Nous avons sélectionner deux instants sur le graphique :
L’un à environ 8,2 secondes à partir du début du son, donc avant le passage de la voiture devant le bonhomme vert,
l’autre à environ 9,2 secondes, donc après le passage de la voiture devant le bonhomme vert.
Nous avons fortement zoomer ces deux instants et avons obtenus deux graphiques représentés ci-dessous.
Ci-dessous, trois zoom importants du graphique ci-dessus donnant le temps en centième de seconde.
On voit ainsi sur ces différents graphiques que la fréquence du son qui corespond à sa hauteur dans la gamme musicale change.
Zoom à 8,2 secondes avant le passage de la voiture devant le bonhomme vert 
La partie surlignée en bleu ciel correspondant au temps écoulé entre deux crètes indique sur le logiciel 0,0022 seconde
Cela signifie que le son entendu a une période de 0.0022 seconde qui correspond à une fréquence de 1/0.0022=454 hertz ( Une vibration de l’air de 454 aller et retour en une seconde.
Le premier son émis est un la de 440 hertz. DOnc le son entendu avant le passage de la voiture est un son plus aigu.
Zoom à 9,2 secondes après le passage de la voiture devant le bonhomme vert
La partie surlignée en bleu ciel correspondant au temps écoulé entre deux crète indique sur le logiciel 0,0023 seconde.
Cela signifie que le son entendu a une période de 0.0023 seconde qui correspond à une fréquence de 1/0,0023 = 434 hertz ( une vibration de l’air de 434 aller et retour.
Le premier son émis est un la à 440 hertz. DOnc le son entendu après le passage de la voiture est plus grave.
l
Diagramme des fréquences avec Audacity
Ci-dessous on a placé les diagrammes des fréquences pour deux sons émis la à 440 hertz et mi à 1318 hertz.
Ces diagrammes donnent toutes les fréquences entendues entre 20 et 20 000 hertz avec en ordonnée leur intensité.
Nous prenons les fréquences coreespondant aux trois premier pics. Ils sont marqués en rouge sur chacun des diagrammes.
Les fréquences correspondant sont indiquées en abscisse et aussi dans le rectangle entouré en rouge.
Avant le passage devant le bonhomme


Après le passage devant le bonhomme


Ainsi, on constate là aussi que lesson entendus avant le passage de la voiture sont plus aigus (possèdent une fréquence plus grande) que les sons émis.
Inversement les sons entendus après le passage de la voiture sont plus graves (possèdent une fréquence plus petite) que les sons émis.
Tableau récapitulatif et formules

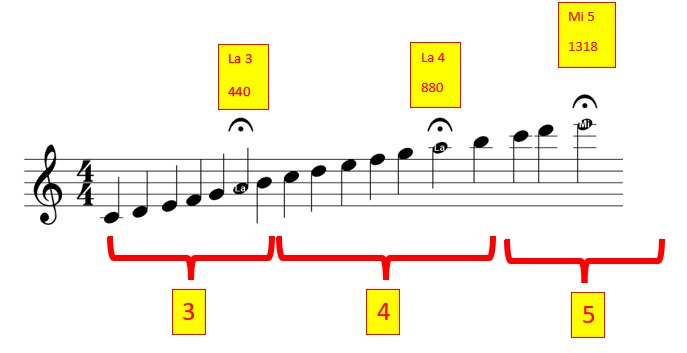
Dans ce tableau les fréquences émises par la sirène, puis les fréquences entendues avant et après le passage de la voiture devant l’observateur (bonhomme vert).
La première fréquence émise correspond à un la3, le la habituel, celui qu’on entend dans l’écouteur d’un téléphone, celui donné par un diapason.
La deuxième fréquence correspond à un la4, une octave plus haute que le la3
La dernière fréquence correspond à un mi5 encore plus haute que le la4
La première gamme vsible sur cette portée est la gamme 3 (Do,Ré,Mi,Fa,Sol,La,Si). Mais avant il existe deux autres gammes avec les mêmes notes mais plus graves.
Après la gamme 3 vient la gamme 4 toujours avec les mêmes notes mais en plus aiguës, puis la gamme 5 incomplète ici faute de place.

LOrsque les vitesses v vont dans le sens de propagation du son eslles sont positives et négatives dans le cas contraire.
On peut déterminer la vitesse ve de l’émetteur donc la vitesse de la voiture si on connaît tous les autres éléments. Ce qui est le cas dans l’exemple que nous utilisons.

Les calculs
Le but est de calculer la vitesse de la voiture en utilisant les données recueillies ci-dessus et résumées dans le tableau.  De la formule donnée ci-dessus nous pouvons déduire :
De la formule donnée ci-dessus nous pouvons déduire :  et en tenant compte du fait que le récepteur (le bonhomme vert) est immobile donc que vr=0 :
et en tenant compte du fait que le récepteur (le bonhomme vert) est immobile donc que vr=0 :
Ainsi dans un premier temps nous calculerons le rapport ( la fraction) des deux fréquences que nous égaliserons avec le reste de la formule pour obtenir une équation dont l’inconnue est ve sachant que la célérité du son dans l’air au niveau de la mer est d’environ 340 m/s ou 340m.s-1
Avant le passage de la voiture devant le récepteur (bonhomme vert)
Calcul avec le la3

La voiture roule dans la même direction que le son émis, de gauche à droite, donc ve est positive.


Après le passage de la voiture devant le récepteur (bonhomme vert)
![]()
la voiture roule de gauche à droite alors que le son arrive par la droite. Ces deux vitesses sont de sens contraire et donc on considère la vitesse de la voiture comme étant négative.



![]()
On observe une légère augmentation de la vitesse qui n’est pas étonnante puisque le chauffaur ne peut que très difficilement garder un vitesse absolument constante.
Calcul avec le la 4 :
La petite différence avec la calcul précédent provient certainement de la précision des mesures et des arrondis dans les calculs. On devrait trouver le même chiffre.

On pourrait faire les mêmes calculs avec le mi 5.
Démonstration de la formule.

Le son émis est une onde avec des crêtes et des creux qui se répètent régulièrement. Le temps écoulé entre deux crêtes (le temps écoulé entre deux pressions maximales d’une lame d’air) est toujours le même et caractérise le son. Ainsi pour le la 440 le temps écoulé entre deux crêtes est de 22 millisecondes. Ce temps est appelé période et est égal à l’inverse de la fréquence f=440 Hz. Soit donc Te la période du son émis exprimée en secondes.
La crête 1 est émise en premier puis Te secondes après c’est au tour de la crête 2. On pourrait continuer : Te secondes plus tard c’est au tour de la crête 3 puis de la crête 4 non représentées sur le schéma mais qu’on peut imaginer.
Formule donnant la fréquence reçue en fonction de la fréquence émise :

Formule donnant le décalage des fréquences en fonction de la fréquence émise et de la vitesse de l’émetteur.

La même formule mais réduite.

Cliquer sur le bouton bleu « Initialisation »
Au temps t=0 seconde la sirène de la voiture émet la première crête du son.
Au temps t= Te seconde la sirène émet la deuxième crête.
Les deux crêtes sont séparées par un temps de Te secondes correspondant à la période du son et donc à sa fréquence.
Cliquer sur le bouton bleu « Voiture en mouvement ».
On voit clairement les émissions des deux crêtes.
Au cours de ce laps de temps Te on remarque que la voiture a parcouru la distance DE et que la première crête, elle, a parcouru la distance MP.
La distance entre deux crêtes correspond à la longueur d’onde du son émis.
Cliquer sur le bouton bleu « Disatnce »
ve est la vitesse de la voiture, donc la vitesse de l’émetterur du son.
c est la célérité du son, la vitesse à laquelle le son se propoage.
Distance parcourue par la voiture : sa vitesse multipliée par le temps Te :![]()
Distance parcourue par la première crête ; vitesse du son multiplié par Te :![]()
Longueur d’onde, distance entre deux crêtes :![]()
![]()
La fréquence reçue fr par le récepteur est égale à la vitesse de propagation du son c divisée par la longueur d’onde dont on connaît la valeur . (Cf les formules à savoir en début de ce chapitre) 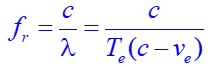

or l’inverse de la période émise 1/Te est égale à la fréquence émise fe.
A partir de là, on peut calculer le décalage (la différence) Δf entre la fréquance reçue fr et la fréquence émise fe ;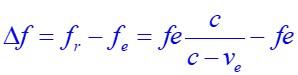

ou en réduisant au même dénominateur :
