Le son
- par gabriel
- dans Articles nouveaux, phénomènes périodiques, Physique
- sur 22 février 2024
Pour commencer, une animation
Dans l’animation ci-dessous Un conseil ne met pas le son de ton appareil trop fort.
régle le curseur sur 0.5; clique sur « Animation »; clique aussitôt sur « Ecouter le son ». Regarde écoute, comprend ce qui se passe. Clique sur « Initialisatin/arrêt ».
Régle le curseur sur 1;recommence le processus.Puis régle le curseur sur 1,5……………jusqu’à 7.
Le son n’est pas intégré dans l’animation pour éviter d’avoir mal aux oreilles à force. On peut choisir de ne pas l’écouter.
La vibration de la colonne dair en bleu ne correspond pas à la réalité du son. Elle devrait vibrer infiniment plus rapidement.
Le point Q correspond à un point de la colonne d’air mais dont le déplacement, la vibration est en quelque sort étiré dans le temps.
La courbe rouge finale correspond à cet étirement du déplacement du point Q sur l’axe du temps.
Une crête ne correspond pas du tout au sommet d’une vague c’est un instant, l’instant où le point Q est au sommet de la corbe.
Finalement c'est quoi le son ?
Le son est une vibration.
lorsque tu chantes une note et que tu mets ta main sur ton cou, tu sents une vibration.
Le haut parleur de l’animation possède une membrane qui vibre. Tu sens cette vibration si tu mets ta main dessus.
La membrane qui vibre dans le haut parleur tranmet cette vibration à la toute petite colonne d’air qui la jouxte.
La petite colonne d’air transmet sa vibration à la petite colonne d’air voisine et ainsi de suite.
On a ainsi des petites colonnes d’air qui vibrent.
La petite colonne d’air qui touche ton tympan fait vibrer celui-ci, qui fait vibrer les petits os de l’oreille interne. Un nerf réceptionne ces vibrations et les transforme en courant électrique qui est acheminé dans ton cerveau. Ton cerveau traduit cette succession de phénomènes en quelque chose de plus ou moins agréable suivant ce que le haut parleur émet.
Les caractéristiques du son.
Pression, puissance acoustique.
Règle le son de ton appareil pour qu’il soit moyennement audible.
Règle le curseur sur 0,5.
Clique sur « Ecouter le son ».
pendant que le son s’éxécute tu peux faire varier le curseur.
Equation donnant l’ordonnée du point vibrant Q (voir animation ci-dessus) en fonction du temps t en seconde. La graduation nous donne des millisecondes. L’intensité, la pression sonore ou acoustique varie avec le curseur. ![]()
La pression acoustique d’un son est la pression qu’exerce ce son sur ton tympan. Le fait que le son est une vibration, celle-ci lorsqu’elle arrive sur le tympan exerce sur lui une pression.Elle se mesure comme toute pression en Pascal.
Sa mesure s’étale de 20 micro Pascals, 20 μPa à quelques dizaine de Pascals. C’est une échelle très grande c’est la raison pour laquelle on utilisera une échelle logarithmique dont l’unité sera le Bel.
Cette échelle donnera le niveau de la pression acoustique.
Comme le Bel est une grande unité, on en utilisera seulement le dixième donc des décibels dB
Formule donnant le niveau de pression acoustique :![]()
Le p de la pression est un petit p minuscule.
De même on peut calculer la puissance acoustique en Watts qui correspond à la puisance nécessaire que devra fournir l’émetteur (voix, haut,parleur) pour émettre le son.
Rappelons que la puissance en Watts est égale à une fource en newton exercée pendant une seconde.
Là encore l’échelle est trop importante et on utilisera aussi les logarithmes décimaux.
Formule donnant le niveau de la puissance acoustiqiue : 
Le P de la puissance est un grand P majuscule.
Intensité sonore, niveau d'intensité sonore ou acoustique.
Représentation de la vibration de la colonne d’air qui est en réalité la vibration d’une surface sphérique se propageant.
La première vspfère vibre, propage sa vibration par contiguïté à la deuxième sphère qui la propage à son tour à la troisième sphère. Les molécules d’air vibrent mais ne se déplacent pas. La propagation se fait sans déplacement de matière. Elle se fait à lavitesse du son dans l’air.

L’intensité sonore I en Watt.m-2 est proportionnelle à la puiisance sonore P en watts et inversement proportionnelle à la surface S en m2 de l’onde.

Formule du niveau de l’intensité sonore en décibels.

La mince colonne d’air qui vibre est en fait la surface d’une sphère. (Nous avons représenté ci-contre les surfaces de demi-sphères. Il était trop compliqué de représenter des sphères entières imbriquées les unes dans les autres. )
Autrement dit c’est la mince couche de la surface d’une sphère qui vibre et qui transmet de proche en proche sa vibration. Attention c’est uniquement la surface de la sphère qui vibre et non pas toute la sphère, toute la boule.
Si r est le rayon de la sphère, 2r=d en sera son diamètre et la sa surface sera égale à : ![]()
Intensité sonore :
L’intensité sonore en watts par mètres carrés est égale à la puissance sonore en watts divisée par la surface de la sphère en mètres carrés. 
En S1 la puisance sonnore est répartie sur une petite surface
En S2, la puissance sonore est répartie sur une plus grande surface.
Donc l’intensité sonore sera plus faible qu’en S1(On divise un même nombre P par un plus grand nombre S2)
En s’éloignant de la source l’intensité sonore diminue.
Cette intensité sonore n’est audible que pour I0=10-12 watts par m2 : I0=10-12 W.m-2.
Cette i,tensité est audible sans douleur pour les oreilles jusqu’à Imax=102.m-2 W.m-2.
On a donc une échelle de valeurs pour I allant de 10-12 à 102
(0,000 000 000 001 à 100)
C’est une échelle beaucoup trop grande. On aura donc recoure aux logarithmes décimaux pour formuler le niveau d’intensité sonore L dont l’unité sera le Bel. L’intensité sonore sera exprimée en décibel (en dixième de Bel).
Fréquence f
Règle le son de ton appareil.
Règle le curseur à 110.
Clique sur « Ecouter le son « .
Tu peux faire glisser le son tout en écoutant.
Pour ne pas abimer tes oreilles le son n’est émis que pendant 10 secondes
La période en secondes est l’inverse de la fréqence en Hertz.
La fréquence en Hertz est l’inverse de la période en secondes.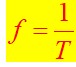
Période :
le temps T = A’B’ qui s’écoule entre deux crêtes (deux instants ) A’ et B’ est égal au temps qui s’écoule entre A et B. Ce temps est appelé la période dont l’unité est la seconde.
Fréquence :
L’inverse de cette période T correspond au nombre d’aller et retour (nombre de crêtes) qui se produit en une seconde. Ce nombre d’aller et retour de la vibration est la fréquence f mesurée en Hertz.
Plus la période T est faible, plus la fréquence f est grande et plus le son est aigu.
Plus la période T est grande, plus la fréquence f est faible et plus le son est grave.
Longueur d'onde
La longueur d’onde λ est égale au déplacement de l’onde pendant la durée T d’une période.
Initialise l’application fci-dessus en cliquant sur le bouton « initialisation »
Règle le curseur sur 20. Tu peux écouter le son correspondant, c’est un son très grave, c’est le son le plus grave que notre oreille peut entendre.
Clique sur le bouton « Afficher les périodes T ». L’onde correspondant à 20 Hertz (20 aller et retour) s’affiche. Tu peux lire sa période T = 0,05 secondes.
L’axe des abscisse est gradué en seconde et l’unité correspond à une seconde.
Tu vois sur le graphique que la distance ABf=A’fB’f correspond bien à 0,05 seconde.
Pendant ces T=0,05 seconde l’on,de s’est propagée de λ=17,2 m.
Clique sur « Afficher les longueurs d’onde ». L’axe des abscisses est gradué en mètres et l’unité correspond à 1 mètre.
Tu vois apparaître le graphique de l’onde. Mais pour cette valeur, tu ne peux pas voir la voir sur le graphique car 17,2 mètre est situé bien au delà de la page.
Tu recommences en réglant le curseur sur 130 Hertz.
Pour les fréquences tu vois que les crêtes se rapprochent beaucoup.
Par contre tu peux voir la longueu d’onde sur le graphique.
Tu peux recommencer autant de fois que tu veux jusqu’à 4400 Hertz.
Les fréquences sont tellement petites pour l’échelle choisie que les cr^tes se touchent sur le graphique et on ainsi un bandeau vert.
Par contre tu visualise très bien la longueur d’onde.
Sons simples, sons complexes, harmoniques.
Son simple
Un son simple est représenté par une sinusoïde.
Ci contre le son simple de toute la gamme chromatique.
Do, Do#, Ré, Ré#, Mi, Fa,Sol,SOl#, La, La#, Si, Do.
Règle le curseur à l’extrémité gauche a=261,6
Cela corespond à la note Do (octoave 3).
Pour entendre le son clique sur le bouton son. Tu l’entends pendant 20 secondes. Si le son s’arrête tu peux cliquer à nouveau sur le bouton.
La sinusoïde du Do est visible en rouge.
Fait glisser le curseur vers la droite cran par cran.
Tu entends et tu vois la sinusoïde de chacune des notes de la gamme chromatique (celle qui monte de demi ton en demi ton avec les dièses ou les bémoles.
Son complexe
Un son complexe, c’est, comme son nom l’indique, plus compliqué.
Il est représenté par une courbe qui ne ressemble pas du tout à une sinusoïde, mais elle est périodique puisque le même motif se reproduit régulièremet.
Utilise l’animation ci-dessous pour étudier un son complexe.
Tout d’abord règle le volume du son de ton appareil à moyen pour ne pas t’habiber les oreilles.
Clique sur « initialisation »
Règle avec le curseur « durée du son en secondes « . Sur 5 tu entendras le son pendant 5 secondes. Sur 0 tu ne l’entendras pas à part un petit claquement.
Clique sur « Son » .
Tu vois apparaître une courbe qui représente le son que tu entends. Si tu as l’oreille fine tu entends que ce son a une certaine propriété quon va étudier.
Rendez-vous sous la fenêtre de l’animation.
Le son représenté a une période de 2,27 milliseconde et donc une fréquence de 440 hertz. Tu peux vérifier la période sur le graphique.
Tout son complexe peut-être décomposé en plusieurs sons simples (représentés par des sinusoïdes)
La première possède la même fréquence que le son complexe. On l’appelle la fondamentale. Ici 440 hertz. Clique sur « Fondamentale ».
La fréquence de la deuxième appelée première harmonique est le double la fondamentale soit ici 2 x 440=880 hertz. Clique sur « Harminique 1 ».
La fréquence de la troisième, deuxième harmonique pour est le triple de la fondamentale soit 3 x440 = 1320 Hertz. Clique sur « Harmonique2 ».
Et ainsi de suite pour les harmoniques suivantes. Clique tou à tour sur ‘harmonique3″, « harmonique' », …., jusqu’à « harmunique 8 ».
En effectuant la somme de etoutes ces sinusoïdes on optient la corbe rouge qui représente le son du départ qui est la synthèse de tous les sons simples optenus.
Petite précision: Le son de départ a été émis par ma clarinette. C’est un si sur ma clarinette, mais en réalité la vraie note est un la à 440 hertz. En effet, la clarinette est un instrument de musique transpositeur. C’est une clarinette en si bémol. Cela suinifie que lorsque je fais un do sur ma clarinette c’est en réalité un si bémol. Donc pour avoir un vrai la 440 j’ai dû fair un si sur ma clarinette. Il existe aussi des clarinette en la et en mi bémole.
Les harmoniques de mon si clarinette sont beaucoup plus nombreux. J’ai dû prendre les premiers pour ne pas surcharger l’animation. C’est la raison pour laquelle le son de la clarinette est peu différent de la fondamentale.
Ci -dessous toutes les harmoniques son représentées par des pics pointant vers le haut. La fondamentale est représentée par le premier pic à gauche. 
Spectre sonore

Spectre Sonore de la note si émise par une clarinette en sib donc en réalité la note la
Pour chaque instrument de musique, on représente les différents harmoniques avec leur intensité sonore par un graphique, le spectre sonore.
Ci-contre : le spectre sonore de la note si de la clarinette en sib.
En abscisse les fréquences de 0 à 4000 Hertz. Elles sont indiquées en plus en haut de chacune des fréquences avec la note correspondante.
On remarque qu’on a multiplié par la suite des entiers naturels (1,2,3,….) la fréquence fondamentale ( la première fréquence à 440 Hertz)pour obtenir les différentes harmoniques.
Lorsqu’on multiplie la fondamentale par une puissance de 2 (2,4,8…) on obtient la même note mais une octave plus haute.
En ordonnée : les intensités en watt.m-2 de chacune des fréquences ou les niveaux d’intensité en dB (décibell). Ici en dB à partir du niveau -70 dB.
Ainsi chaque instrument de musique aura sa particularité sonore traduite par son spectre sonore. Il peut arriver que certaines harmoniques n’existent pas dans le spectre.
Pour les niveaux d’intensité sonore ou l’intensité on s’apperçoit que dans ce cas l’harmonique la plus intense est la fondamentale et la moins intense est la fréquence 2640 Hertz.
Le spectre sonore d’une note d’un instrument de musque traduit ce qu’on nomme son timbre. Le timbre de la clarinette est différent de celui du piano, du hautbois, de la trompette…..