Statistiques introduction
- par gabriel
- dans Mathématiques, Statistiques
- sur 3 juin 2019

Approche par un exemple
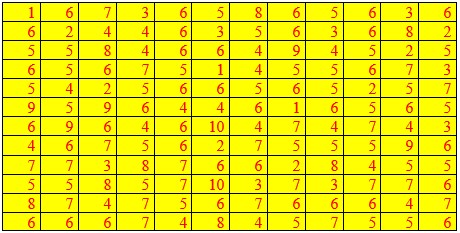
On veut étudier le nombre de graines dans une gousse de haricots.
On récupère 144 gousses de haricots :on compte et on note le nombre de graines qu’on trouve à l’intérieur. On obtient ainsi une série de nombres qu’on aurait pu écrire à la suite les uns des autres mais qu’on a inséré dans un tableau.
Moyenne
![]()
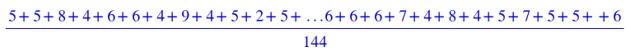
Je voudrais savoir combien, en moyenne, une gousse pourrait contenir de graines.
Pour cela il nous suffit d’additionner tous les nombres de cette série et de diviser par le nombre total de gousses soit 144.
C’est un peu fastidieux ! non ?
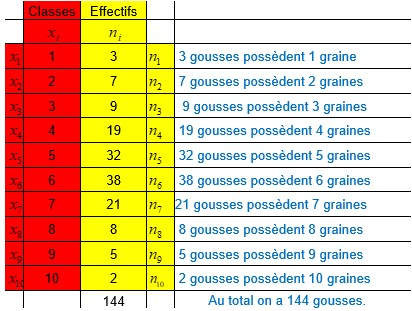
le petit i est un indice. Dans cet exemple
il prend les valeurs de 1 à 10.
x1=1 la classe 1 a pour valeur 1
n1=3 l’effectif de la classe 1 est égal à 3.
Dans la classe des gousses de haricot possédant 1 graine, il y en a 3. Trois gousses possèdent une graine.
On s’aperçoit finalement que au minimum un haricot possède une graine et au maximum 10 graines.
Ainsi on peut faire une colonne du nombre de graines de 1 à 10 et marquer en face le nombre de gousses possédant ce nombre de graines
Ainsi on aura une colonne xi dans laquelle sont inscrits les nombres de graines.
Dans une seconde colonne ni on notera le nombre de gousses qui possèdent xi graines.
La colonne des xi s’appelle les classes.
La colonne des ni s’appellera les effectifs. C’est le nombre d’éléments dans chacune des classes.
![]()
![]()
![]()


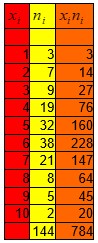
On rappelle que l’on veut calculer la moyenne, c’est-à-dire le nombre moyen de graine qu’il y a dans une gousse de haricot.
i=1 3 gousses possède 1 graine donc 3×1=3 graines.
i=2 7 gousses possèdent 2 graines donc 7×2=14 graines.
i=3 9 gousses possèdent 3 graines donc 9×3=27 graines.
i=4 19 gousses possèdent 4 graines donc 19×4=46 graines.
i=5 32 gousses possèdent 5 graines donc 32×5= 160 graines.
i=6 38 gousses possèdent 6 graines donc 38×6=228 graines.
i=7 21 gousses possèdent 7 graines donc 21×7=147 graines.
i=8 8 gousses possèdent 8 graines donc 8×8=64 graines.
i=9 5 gousses possèdent 9 graines donc 5×9=45 graines.
i=10 2 gousses possèdent 10 graines donc 10×2=20 graines.
En tout on a 784 graines réparties dans 144 gousses, autrement dit dans les 144 gousses considérées on trouve 784 graines.
Donc en moyenne on aura 784:144 graines par gousse soit 5,45 graines par gousse.
Ne soyons pas surpris d’avoir un nombre décimal. Nous venons de calculer une moyenne.![]() est la lettre grecque majuscule sigma. Ce symbole signifie en mathématiques somme de.
est la lettre grecque majuscule sigma. Ce symbole signifie en mathématiques somme de.![]() une barre au dessus d’une lettre signifie moyenne.
une barre au dessus d’une lettre signifie moyenne.
Effectifs cumulés
Effectifs cumulés croissants
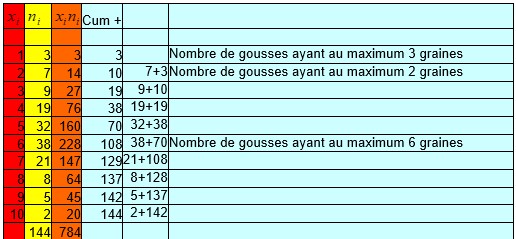
On voudrait connaître le nombre de gousses de haricots qui possèdent au plus, au maximum 4 graines.
Pour cela, il suffit d’ajouter
le nombre de gousses contenant 1 graine plus
le nombre de gousses contenant 2 graines plus
le nombre de gousses contenant 3 graines plus
le nombre de gousses contenant 4 graines.
Mais on peut ajouter une colonne à notre tableau précédent dans laquelle on ajoute à chaque ligne l’effectif de la ligne précédente.
On cumule de ligne en ligne l’effectif de la ligne en question avec la ligne précédente.
Effectifs cumulés décroissants

On voudrait connaître le nombre de gousses possédant au moins 3 graines autrement dit 3,4,5,6,7,8,9,10 graines.
Pour cela il faut ajouter les 8 lignes d’effectifs ci-dessus ou bien soustraire à 144 le nombre de gousse possédant 2 graines et le nombre de gousses possédant 1 graines.
On va donc construire une cinquième colonne en soustrayant chaque fois à la ligne précédente l’effectif de la ligne en question.
Fréquences
Fréquences : décimaux, fractions, pourcentages
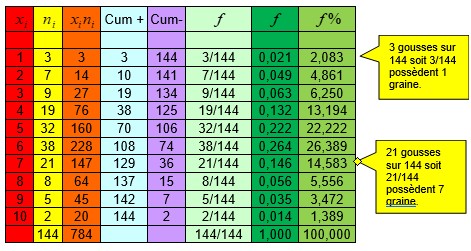

Pour x1 3 goussent sur 144 possèdent une graines. A partir de cette constatation, nous pouvons engendrer un nombre supplémentaire qu’on appellera la fréquence.
Cette fréquence peutêtre exprimée en fraction, en nombre décimal ou en pourcentage.
Ainsi pour x1 ![]()
Pour x7 ![]()
en arrondissant au millième.
Fréquences cumulées

A partir des fréquences exprimées en décimaux on peut rajouter deux colonnes l’une pour les fréquences cumulées croissantes et l’autre pour les fréquences cumulées décroissantes.
On peut faire la même chose pour les fréquences exprimées en pourcentage.
On obtient le tableau ci-contre.
Médiane
On veut connaître maintenant pour quel nombre de graines on a la moitié des effectifs en dessous et la moitié des effectifs au-dessus.
Il nous faut trouver le la classe xi tel que la somme des ni avant cette classe soit égale à la moitié de l’effectif total ou tel que la somme des ni après cette classe soit égale à la moitié des effectifs. C’est un peu difficile à traduire en français simple, mais voyons ce que cela donne avec notre exemple.
Il nous faut tout d’abord classer les gousses par ordre croissant.

Approche empirique
La moitié de l’effectif total est![]()
Il nous faut trouver dans quelle classe (dans quelle gousse) se trouve la 72ième graine de haricot (après qu’on ait trié et rassemblé les haricots semblables, c’est-à-dire ceux qui contiennent le même nombre de graines ).
Dans le schéma ci-dessus on a trié les gousses (les classes) suivant le nombre de graines qu’elles contiennent. Ainsi on a 3 gousse ayant 1 graine (111) puis 7 gousses ayant 2 graines (2222222) puis 9 gousses ayant 3 graines (333333333) etc.
On s’aperçoit en comptant que la 72ième graine se situe dans la classe des 6, c’est à dire dans une gousse contenant 6 graines et plus précisément dans la deuxième gousse de 6 graines. Notre médiane est donc égale à 6.
En utilisant le tableau

Si on utilise la colonne des effectifs cumulés croissants, on remarque que jusqu’à la classe 5 on a 70 graines. Donc la 72ième graine se situera dans la classe 6.
Si on utilise la colonne des fréquences cumulées croissantes, on note que la moitié de 1 est 0,5. Jusqu’à la classe 5 on a une fréquence cumulée de 0,486. Donc 0,5 sera dans la classe 6.
De même si on utilise les fréquences cumulées croissantes en pourcentage, jusqu’à la classe 5 on a 48,611% des graines. Donc l pour atteindre la moitié des graines (50%) il faut aller jusqu’à la case 6. La médiane est donc égale à 6.
Précision
Si l’effectif total est un nombre impaire, la moitié d’un nombre impaire est égale à un nombre décimal. Si on avait par exemple 145 graines, la moitié est égale à 72,5 graines. Dans ce cas on arrondit à 73. Ce qui ne change pas grand chose.
Quartiles
Avec la médiane on a défini la classe délimitant la moitié (50%) des effectifs.
On peut faire de même avec une classe délimitant le quart (25%) des effectifs. C’est le premier quartile
On peut encore faire de même avec une classe délimitant les trois quarts (75%) des effectifs. C’est le troisième quartile.

Pour le premier quartile,![]()
on doit repérer dans quelle classe se trouve la 36ième gousse.
En comptant, on trouve la classe 4.
Pour le troisième quartile,![]()
on doit repérer dans quelle classe se trouve la 108ième gousse. On trouve la classe 6.
Pour éviter de trier les gousses dans l’ordre croissant, ce qui est fastidieux, on utilise le tableau ci dessous :

Le premier quartile est situé à la 36ième gousse On voit dans la colonne des effectifs cumulés croissant que cette 36ièùe gousse est située dans la classe 4.
En utilisant les fréquences cumulées croissantes, on repère 0,25 qui se trouve dans la classe 4
En utilisant les fréquences cumulées croissantes en pourcentage, on repère 25% qui se trouve bien dans la classe 4.
Pour le troisième quartile la 108ième gousse est dans la classe 6.
En utilisant les fréquences : on repère 0,75 et 75% qui sont bien dans la classe 6.
Variance
La moyenne est insuffisante
Revenons à la moyenne :
Il y a une infinité de façons d’obtenir une moyenne de 10 avec deux notes.
Prenons en 2 :
première possibilité : un élève a eu un 0 et un 20.
![]()
Deuxième possibilité : un autre élève a obtenu un 8 et un 12.![]()
Dans le premier cas l’écart des deux notes à la moyenne est important la différence est de 10 points
Dans le second cas l’écart à la moyenne est moins important, la différence est de 2 points.
La moyenne nous renseigne donc sur une série statistique mais ce n’est pas suffisant. Il nous faut mesurer comment chaque valeur est situé par rapport à la moyenne, de combien elle s’en écarte.
Connaître les écarts à la moyenne de chacune des valeurs serait fastidieux. Par contre on pourrait calculer la moyenne de ces écarts à la moyenne
Dans notre premier cas la moyenne des écarts à la moyenne est de 10 points et dans le second cas de 2 points.
Mais nous remarquons que si nous calculons cet écart à la moyenne uniquement en effectuant la soustraction entre la valeur et la moyenne nous obtenons soit des nombres positifs soit des nombres négatifs. Or pour calculer une moyenne on a besoin d’additionner des nombres positifs.
Pour cela on peut par exemple prendre la valeur absolue de la différence.
Mais les statisticiens ont préféré élever cette différence au carré.
(valeur –moyenne)² ; (12-10)² >0 (8-10)² >0
En additionnant les carré des écarts à la moyenne de toutes les valeurs et en divisant par l’effectif total on obtient un nombre qui nous renseignera sur la dispersion moyenne des valeurs autour de la moyenne : c’est la variance.
La variance est donc la moyenne des carrés des écarts à la moyenne de la série statistique étudiée.
Méthode de calcul
Plutôt que de prendre une par une toutes les données du premier tableau, on va utiliser le tableau récapitulatif en ajoutant des colonnes.
pour la commodité nous supprimons les colonnes qui ne nous servent pas dans ce calcul.
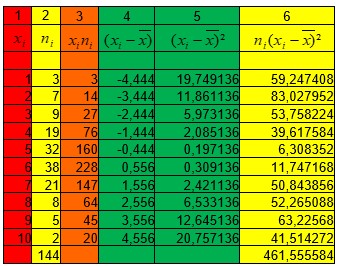

La moyenne ![]() calculée au début de cette page est 5,444.
calculée au début de cette page est 5,444.
Colonne 1 : nombre de graines dans une gousse xi.
Colonne 2 : nombre de gousses ni ayant xi graines.
Colonne 3 : Nombre de graines xini dans les ni gousses.
Colonne 4 ; écart à la moyenne du nombre de graines dans une gousse.
1-5,444 ; 2-5,444 ; 3-5,444 ; 4-5,444 ; 5-5,444 ; 6-5,444……….
Colonne 5 : Carré de cet écart à la moyenne.
(1-5,444)² ; (2-5,444)² ; (3-5,444)² ; (4-5,444)² : (5-5,444)² ;
(6-5,444)²
Colonne 6 ; Carré des écarts à la moyenne pour ni gousses.
3(1-5,444)² ; 7(2-5,444)² ; 9(3-5,444)² ; 19(4-5,444)² ;
32(5-5,444)² ; 38(6-5,444)² …
La somme de la colonne 6 est égale 461,555584
La variance est donc 461,555584/144= 3,21.
Autre méthode
On peut utiliser une autre façon beaucoup plus simple sachant que les deux formules données sont équivalentes.


Colone 1 : Nombre de graines xi dans une gousse
Colone 2 : Nombre de gousses ni ayant xi graines.
Colone 3 : Nombre de graines xini dans les ni gousses.
Colone 4 : le carré des xi. Nombre de graines dans une gousse au carré.
Colone 5 : carré de xi multiplié par ni.
La somme des nixi² de la case 5 est 4730.
L’effectif total, la somme des ni est 144.
On divise 4730 par 144. On obtient 32,847222.
On soustrait à ce chiffre le carré de la moyenne 5,444²
On obtient environ compte tenu des arrondis 3,21.
Ecart type

La variance nous donne le carré de la moyenne des écarts à la moyenne, autrement dit le carré de la dispersion moyenne autour de la moyenne.
L’écart type ,lui nous donnera la moyenne des écarts à la moyenne et non plus le carré.
L’écart type est donc égal à la racine carrée de la variance. Il est représenté par la lettre grecque ρ (rho).
Dans notre exemple l’écart type est :![]()
Histogramme
Nous pouvons représenter notre série statistique sur des graphiques.
Nombre de gousses possédant n graines
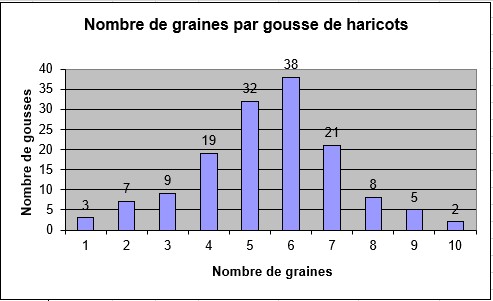
Sur ce graphique, appelé histogramme le nombre de graines dans chaque classe est représenté par un rectangle dont la largeur représente la classe et la longueur le nombre de graines dans la classe.
On voit que 3 gousses possèdent 1 graine, que 7 gousses possèdent 2 graines. …..
Les valeurs des classes xi sont :
1 ;2 ;3 ;4 ;5 ;6 ;7 ;8 ;9 ;10
A chacune des classes correspond un effectif ni.
Pour la classe 7 l’effectif correspondant est 21.
Effectifs cumulés croissants et décroissants
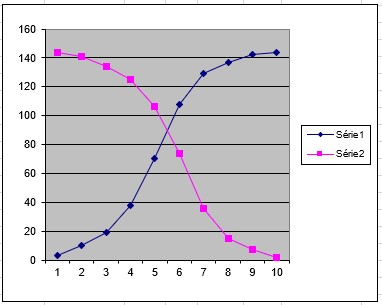
Ce graphique représente les effectifs cumulés croissants en bleu et les effectifs cumulés décroissants en rose.
A l’intersection des deux courbes se troue la médiane (6,72)
Fréquences cumulées croissantes et décroissantes
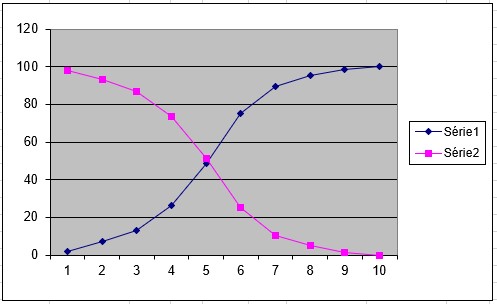
En bleu, les fréquences cumulées croissantes.
En rose, les fréquences cumulées décroissantes.
Autre représentation, le camembert.
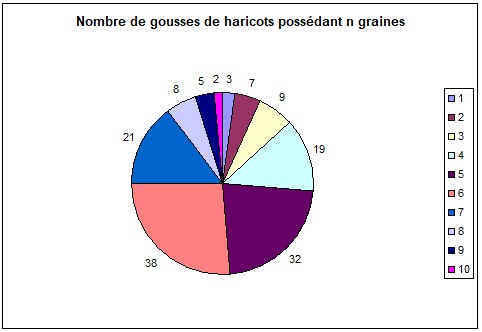
Le nombre de gousses xi contenant ni graines est représenté proportionnellement à la valeur ni sur un cercle.