Les nombres complexes
Sommaire
Pourquoi d'autres nombres
- Imaginons trois affirmations équivalentes qui sont absurdes dans l’ensemble des Nombres Réels
Il existe un nombre k tel que
Tout élément de l’ensemble des réel possède une racine carrée
Toute équation du second degré possède une solution.
Il est bien évident que le nombre k n’appartient pas à l’ensemble des réel,
comme il est évident que la racine carrée d’un nombre négatif n’appartient pas à l’ensemble des réels
ainsi que les solutions d’une équation du second degré dont le discriminant est négatif.
Puisque ces nombres n’appartiennent pas à l’ensemble des réels, il nous faut construire ( inventer) un autre ensemble qui les contiendra.
Cet ensemble s’appelle l’ensemble des nombres complexes pour lequel on a inventé un nouveau nombre i tel que i² =-1.
Ce nombre est imaginaire d’où i.
Nous aborderons plus tard les détails de la construction de ce nouvel ensemble : le corps des nombres complexes.
Définition
L’ensemble des nombres complexes est un ensemble nommé 
contenant tous les éléments de l’ensemble des réel tel que
– il existe un élément de cet ensemble appelé i tel que i²=-1
– tout élément de s’écrit 
a et b étant des réels.
– est muni d’une addition et d’une multiplication qui suit les mêmes règles que dans
-Un nombre complexe est en général représenté par la lettre petit z ,
.
Ainsi tout nombre complexe possède deux parties
– une partie réel a 
– une partie imaginaire 
généralement précédée ou suivie du nombre i
: cette écriture est appelée forme algébrique .
Egalité
Deux nombres complexes sont égaux si leur partie réel et leur partie imaginaire sont respectivement égales
soit :
et 
si 
et 
Soit deux nombres complexes dont l’un d’eux est inconnu, le deuxième :
si 
Addition et soustraction
Le corps des complexes est muni d’une première opération l’addition qui est la même que celle des réelles. Donc les règles ne changent pas.
Soit deux nombres complexes :
Posons l’addition comme dans les réels :
Regroupons les parties réelles et les parties imaginaires :
Dans la partie imaginaire factorisons par i 
Voilà c’est fait. Il suffit d’additionner les parties réelles ensembles et les parties imaginaires ensembles.
Pour la soustraction, il suffit d’appliquer la règle des signes utilisée dans l’ensemble des Réels.
Voyons un exemple 
Multiplication
On utilise les règles utilisées dans l’ensemble des Réels, les règles de la distribution (développement) avec une particularité très importante :
on remplace toujours et tout de suite 
par 
.
On obtient un produit de facteur. Il suffit de développer :
On remplace tout de suite par et on met i en facteur 
On rassemble les parties réelles et imaginaires:
On a ainsi le résultat.
Exemple : soit les deux nombres complexes
Conjugué d'un complexe
Rappel :
Dans l’ensemble des réels nous savons que ;
est le conjugué de 
Et inversement
Cette notion sert particulièrement à éliminer les racines carrées du dénominateur d’une fraction.
Dans l’ensemble des complexes on peut trouver :
est le conjugué de 
et inversement
Ainsi 
est le conjugué de 
se dit z barre (ne pas confondre avec les probabilités, cela n’a rien à voir).
Cette notion va nous permettre d’éliminer les 
au dénominateur d’une fraction.
Rendre un dénominateur réel
Rendre un dénominateur réel 
la partie imaginaire du dénominateur nous empêchera ensuite d’effectuer éventuellement des calculs simples
On va donc essayer de se débarrasser de cette partie imaginaire du dénominateur en le multipliant par son conjugué .
pour conserver la même valeur à la fraction, il faut multiplier le numérateur aussi par la cette quantité conjuguée.
Ensuite on effectue les calculs au numérateur et au dénominateur. 
On réduit en remplaçant par 
Voyons avec un exemple concret :
Conjugué d'un complexe
Propriété des nombres complexes conjugués :
Le conjugué d’une somme est égal à la somme des conjugués :
Soit les deux nombres complexes 
Leur somme est 
Le conjugué de leur somme est :
Le conjugué de est 
Le conjugué de est 
La somme de ces deux conjugués est 
soit
Le conjugué d’un produit est égal au produit des conjugués.
Je te laisse le soin d’en faire la démonstration.
Le conjugué d’une puissance est égal à la puissance du conjugué. 
C’est évident puisque l’opération puissance est une suite de multiplications d’un même nombre.
Le conjugué de l’inverse d’un nombre est l’inverse de son conjugué. 
Le conjugué du rapport de deux nombres complexes est égal au rapport des conjugué de ces deux nombres à condition que celui qui est au dénominateur ne soit pas nul.
Inverse et division
Inverse :
L’inverse de
est
Comme on a au dénominateur, pour le supprimer, on multiplie le dénominateur
par sa quantité conjugué
ainsi que le numérateur pour ne pas changer la valeur de la fraction 
On développe et on réduit, on obtient 
On peut si l’on veut retenir cette formule, mais on la retrouve facilement.
Division :
il suffit de reprendre la rubrique : rendre réel le dénominateur d’un nombre complexe
Affixe
Repère euclidien (Euclide)
Coordonnées cartésiennes (Descartes)
Soit un repère orthonormé :
les deux axes x’ox et y’oy sont orthogonaux ( perpendiculaires)
Les normes (longueurs) des vecteurs unitaires (représentant l’unité, le 1) sur chacun des axes sont égales.
Les coordonnées d’un point s’écrivent :
Les coordonnées du vecteur OA s’écrivent :
Plan complexe
Deux axes perpendiculaires.
Lun x’ox est appelé axe des réels
L’autre y’oy est appelé axe imaginaire
Affixes particulières
Affixe d’un vecteur quelconque
Soient A et B les points d’affixes respectives :
L’affixe du vecteur 
sera égale à l’affixe du point B moins l’affixe du point A
Pour le cas particulier :
Affixe du milieu d’un segment
Soient A et B les points d’affixe respectives :
L’affixe C du milieu du segment AB sera égale à la demi somme des affixes de A et B.
Exemple de problème résolu avec les complexes
Soit une plaque de fer ABCD disposée sur un repère orthonormé et dont sur les sommets sont collées respectivement des masses de 1,2,3 et 4 kg en rouge sur fond jaune sur le croquis.
Trouver les coordonnées de son centre de gravité.
Rappel : Le centre de gravité est le point fictif où se concentre tout le poids d’un objet. Un objet posé sur une aiguille en son centre de gravité reste en équilibre.
Ce problème peut se traiter par la notion mathématique de barycentre.
Le barycentre de 4 points affectés des coefficients 
est tel que :
Dans notre cas particulier on aura : 
Traduisons cela en termes de nombres complexes :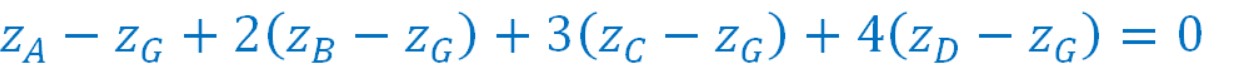
Nous avons sur le graphique les affixes des points A,B,C et D :
Il ne reste plus qu’à remplacer et calculer sachant que nous cherchons les coordonnées du point G :
Ainsi on peut placer le point G sur le graphique :
Forme trigonométrique d'un nombre complexe
Voyons avec un cas particulier :
Soit le point M d’affixe :
représenté sur la figure ci-contre.
La longueur r= OM s’appelle le module de z :
Calculons ce module de z dans le triangle rectangle OMC :
OM²=MC²+OC² =a²+b²
Calculons maintenant les cosinus et sinus de l’angle têta :
On en déduit les valeurs de a et b:
En rempaçant a et b par ces valeurs, on obtient :
en factorisant :
Ou en remplaçant z :
Soit le point M d’affixe 
Pour écrire ce nombre sous forme trigonométrique, il nous faut tout d’abord calculer son module , c’est-à-dire la longueur OM. Si on ne se souvient pas de la formule on se réfère au graphique et on calcul OM avec le triangle rectangle OMC (Ou OMD), OM étant l’hypoténuse de ce rectangle. 
Maintenant il faut calculer son argument, la valeur de l’angle téta.
La aussi on se sert du triangle rectangle. 
Maintenant que nous avons les valeurs du sinus et du cosinus, il faut chercher la valeur de l’angle en radian avec la calculatrice ou avec les tables trigonométriques. 
Comme les valeurs de l’angle sont identiques tout de suite avec le cosinus et avec le sinus, il est inutile d’aller plus loin. 
Et on peut écrire le nombre complexe sous la forme trigonométrique en radian ou en degré :
Autre cas :
Soit le nombre complexe :
Calcul du module :
On peut soit calculer avec les fractions, ce qui est le cas la plupart du temps puisque la fraction est une valeur exacte :
Mais on peut calculer avec les nombres décimaux, c’est ce que nous ferons pour alléger :
Calcul de l’argument :
En fait, il existe deux angles dont le cosinus est -02425 :
Il existe deux angles qui ont pour sinus 0,9701 :
Le résultat sera bien sûr l’angle en commun entre la calcul avec le cosinus et le calcul avec le sinus soit 1,8157 radians.
On en déduit les deux écritures du nombre complexe du départ, l’une en radians et l’autre en degrés. 
Forme exponentielle d'un nombre complexe
Nous avons vu deux formes d’écriture d’un nombre complexe :
la forme algébrique et la forme trigonométrique :
Il nous reste à voir une troisième forme en relation avec le fonction exponentielle.
Le point M est sur le cercle OM=1. Son affixe est z : elle peut être écrite sous forme trigonométrique :
Posons 
Notre nombre complexe est donc maintenant:
Il s’écrit donc très simplement :
Formule d'Euler
On écrit la formule précédente.
On en déduit
Nous connaissons :
En remplaçant
Maintenant que nous possédons les deux valeurs de eiθ et e-iθ , on les additionne membre à membre on réduit et on en déduit la valeur de cosθ.
On procède de la même manière mais en soustrayant membre à membre les deux formules de départ.
Ainsi, nous obtenons les deux formules d’Euler qui sont souvent très utiles dans les démonstrations.
Expression complexe de la translation
Sr l’animation ci-contre les 5 ballons de beaudruche sont en translation du point C au point D suivant la directieon et la longueur du vecteur V.
Dux moyens pour démarrer l’annimation :
soit en cliquant sur le point A et en le faisant glisser sur le curseur rouge de gauche à droite, Si on fait glisser de droite à gauche, les ballons reviennent au point de départ C.
soit en cliquant sur la petite flèche noire siruée en bas à gauche . Les ballons se diigent vers le point D et lorsqu’ils l’ont atteint, ils revienent au point de départ C pour recommencer leur translation vers D
Translation d’un point.
Application numérique :
Expression complexe de la rotation
L’animation ci-contre représente la rotation d’une clocha autour de l’axe rouge.
C’est une rotation de 60°.
Deux manières sont possibles pour animer cette cloche.
On peut utiliser le point vert du curseur et le faire glisser le long de ce curseur de gauche à droite On a ainsi la rotation.
Si on fait glisser le pont vert de droite à gauche, la cloche revient à son point de départ.
On peut utiliser la petite flèche noire en bas à gauche en cliquant dessus. La cloche subit alors une rotation de 60° puis revient à son point de départ pour recommencer la rotation.
soit θ≅ 1.05 radians
Dans le graphique ci-contre représentant le plan complexe avec x’Ox l’axe réel d’unité 1 et y’Oy l’axe imaginaire d’unité i on a représenté un point M d’affixe z.
Ce point M subit une rotation de centre Ω d’affixe ω d’angle +θ, puisqu’il est orienté dans le sens trigonométrique (Anti-horaire).
Dans une rotation, les distances des points M et M’ au centre de rotation Ω sont égales 
Ce qui se traduit en prenant les affixes des points M, M’ et Ω :
module de ωz’ = module de ωz 
Ce qui peut s’écrire :
L’angle orienté 
est égal à θ à 2π près.
Ce qui peut se traduire en nombre complexe :
Le nombre complexe :
a pour module 1 et argument θ, donc :
ou en écriture exponentielle :
