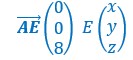Les vecteurs
Sommaire
Vecteur : du latin vehere signifiant conduire, transporter.
Le mot a été introduit en 1925.
La notation 
date de 1920.
Trois notions importantes
Direction.
Deux droites ont même direction, si et seulement si elles sont parallèles.
La direction d’une droite est l’ensemble des droites qui lui sont parallèles. C’est la classe d’équivalence de cette droite pour la relation “est parallèle à”.
Quatre oiseaux survolent la France.
Un rouge-gorge tout rouge qui part de Quimper pour aller à Maubeuge.
Une belle colombe toute blanche qui habitant Bordeaux veut s’installer à Paris.
Un petit colibri jaune qui depuis Clermont-Ferrand veut rendre visite à son cousin à Paris.
Le gros aigle tout noir qui installé sur les hautes montagnes autour de Annecy veut aller voir si la nourriture sera meilleures au dessus de Dax.
La direction du vol du rouge-gorge est la droite (QM).
La direction du vol de la colombe est la droite (BP).
La direction du vol du colibri est la droite (CP).
La direction du vol de l’aigle est la droite (AD).
Bien qu’ils aillent au même endroit, à Paris, la colombe et le colibri n’ont pas la même direction.
Par contre le rouge-gorge et l’aigle qu sont à plusieurs centaines de kilomètres l’un de l’autre, volent avec la même direction.
Les droites (BP); (CP) et (AD) n’étant pas parallèles, n’ont pas la même direction.
Par contre les droites (QM) et (AD) sont parallèles. Elles ont même direction.
Comme il existe une infinité de droites parallèles à une droite donnée, il existe une infinité de droites ayant la même direction.
Sens.
Sur une direction, il existe deux sens.
Arrivés chacun à destination, les oiseaux décident de retourner chez eux où ils sont si bien.
A l’aller le rouge gorge avait volé suivant la direction de la droite (QM). Il allait de Quimper à Maubeuge.
Cette fois il volera suivant la même direction, mais dans le sens contraire de Maubeuge à Qimper (MQ).
La colombe volera dans la même direction qu’à l’aller suivant la droite (BP), mais dans le sens contraire de Paris à Bordeaux (PB).
Le colibri prendra aussi la même direction qu’à l’aller (CP), mais dans le sens contraire de Paris à Clermont-Ferrand (PC).
Enfin l’aigle volera dans la même direction qu’à l’aller (AD) mais dans le sens contraire de Dax à Annecy (DA).
Ainsi sur chaque direction, on a deux sens possibles. C’est ce que la SNCF appelle l’aller et le retour.
Norme, longueur.
La norme est une longueur (Du latin norma=règle)
Le rouge gorge doit parcourir environ 620 km pour retourner à Quimper depuis Maubeuge.
L’aigle doit parcourir le même distance pour retourner à Annecy.
La colombe parcourra 499 km pour retourner à Bordeaux.
Enfin le colibri a une distance de 346 km à parcourir.
Ces distances définissent plusieurs longueurs.
La longueur MQ =QM= 620.
La longueur PB=BP=499
La longueur PC=CP= 346 km
La longueur DA=AD=620 km.
On remarque que la longueur DA est égale à la longueur MQ. L’aigle et le rouge gorge parcourent la même distance.
Définitions d'un vecteur
Ci-dessus, un vecteur en vert avec
– sa direction
– son sens
– sa norme (longueur)
et un de ses représentant particulier nommé : 
La norme d’un vecteur s’écrit : 
Un vecteur est un objet géométrique construit à partir des points, des droites, des longueurs de la géométrie euclidienne et possédant les trois caractéristiques suivantes
– une direction (droite soutenant le vecteur)
– un sens sur cette direction.(deux sens possibles).
– une longueur appelée norme.
Un vecteur n’a pas de place précise dans l’espace ou dans le plan. Un vecteur est donc défini par un représentant, c’est lui qu’on dessine et qu’on nomme. Un vecteur peut avoir plusieurs représentants ( une infinité).
Par la suite, on désignera toujours un vecteur par un de ses représentants.
Ainsi le vecteur vert sera désigné par le vecteur en rouge sur la figure ci-contre.
Considérons deux points A et B. Pris dans l’ordre A puis B, ils déterminent ce qu’on peut appeler un bipoint (A;B).
On remarquera que le bipoint (A;B) n’est pas pareil que le bipoint (B;A).
On considère une relation appelée relation d’équipollence définie ainsi :
Deux bipoints (A;B) et (C;D) sont équipollents si les segments [AD] et [CD] ont même milieu (O sur notre figure).
On peut démontrer que cette relation d’équipollence est une relation d’équivalence qui détermine des classes d’équivalences dans l’ensemble des bipoints.
Ainsi les bipoints (A;B) et (C;D) ont même milieu O.
(A;B) et (K;G) ont même milieu.
(A;B) et (L;H) ont même milieu.
(A;B) et (M;N) ont même milieu.
Mais aussi (K;G) et (L;H).
Mais encore (M;N) et (L;H) ….
On en déduit que les bipoints (A;B) ; (C;D) ; (K;G) ; (L;H) ; (M;N) appartiennent à la même classe dite classe d’équivalence. On peut trouver une infinité de bipoints appartenant à cette classe d’équivalence.
La classe d’équivalence d’un bipoint (A,B) est appelée vecteur , écrit surmonté d’une flèche.
A est appelée origine et B extrémité.
Le bipoint (A;B) est un représentant de cette classe d’équivalence, de ce vecteur. Aucun bipoint n’est privilégié pour être représentant du vecteur. Sauf si on précise son origine.
Les bipoints (A;B) et (C;D) représentent sur cette figure le même vecteur.
On peut écrire : 
Conséquence pratique : on peut construire une vecteur n’importe où dans le plan.
Si on précise l’origine du vecteur, il devra partir de ce point.
Le petit train rouge de montagne monte en suivant ses rails.
Le point A, au bord de la noire cheminée se déplace en même temps que le train jusqu’au point B. On a ainsi un bipoint (A;B).
Il en est de même des points C et D puis E et F qui forment respectivement les bipoints (C;D) et (E;F).
Les points A,C,E subissent un glissement respectivement vers les points B,D,F.
Ce glissement se nomme en mathématique, translation.
On dit que B est l’image de A par la translation (A;B) ou de vecteur .
Cette translation définit une direction, un sens et une longueur.
Vecteur nul, vecteur opposé.
Si le vecteur est réduit à un point A ou B, c’est le vecteur nul. Ce vecteur n’a ni direction ni sens. On le note : 
et on le nomme “vecteur nul”.
Attention 0 est un nombre et est un vecteur. Ne pas confondre.
Tout vecteur 
possède un opposé –=
A la place de –, on peut écrire ce qui est très intéressant pour la suite lorsqu’on aura à additionner ou soustraire des vecteurs, ou lorsqu’on appliquera la relation de Chasles.
Vecteurs égaux
Deux vecteurs sont égaux s’ils ont tous les deux :
– même direction
– même sens
– des normes (longueurs) égales.
C’est le cas des deux vecteurs ci-contre et on peut écrire
D’autre part deux vecteurs et 
sont égaux si et seulement si le quadrilatère ABDC est un parallélogramme.
Autrement dit
Si alors ABDC est un parallélogramme.
Si ABDC est un parallélogramme alors
Somme de deux vecteurs
Première façon : à la queue leu leu 
Nous savons faire la somme de deux nombres, appelés aussi scalaires, mais nous ne savons pas faire la somme de deux objets géométriques.
Cela demande une construction géométrique. Soit 
et 
deux vecteurs du plan. On veut trouver le vecteur 
somme de et de .
Nous savons qu’un vecteur bien qu’il soit défini par sa direction , son sens et sa longueur n’a pas une place particulière dans le plan. On peut construire un représentant du vecteur, n’importe où dans le plan.
Nous allons construire un représentant du vecteur à l’extrémité du vecteur . A cette extrémité on construit un vecteur en pointillé rouge égal au vecteur . (On construit avec le compas). Puis on joint l’origine du vecteur à l’extrémité du nouveau représentant du vecteur . On obtient ainsi la somme des deux vecteurs.
On aurait pu faire la même chose en déplaçant le vecteur à l’extrémité du vecteur pour obtenir un résultat identique. Attention les deux images n’ont pas la même dimension. Il faut compter les carreaux du fond d’image pour constater des résultats identiques.
Signification dans ce cas de la somme de deux vecteurs : parcourir la distance AB puis la distance BC c’est comme parcourir la distance AC. Dans les deux cas on part du point A pour arriver au point C.
Deuxième façon : diagonale d’un parallélogramme. 
A partir d’un point A quelconque du plan, on construit le vecteur , puis toujours à partir de A le vecteur . On obtient ainsi les deux côtés d’un parallélogramme. A partir de A on trace sa diagonale. C’est la somme = +. On lit “vecteur W= vecteur U + vecteur V”.
Interprétation:
Deux enfants Victor et Hugo se disputent la même locomotive. Victor, l’aîné et le plus fort tire la locomotive dans la direction et avec la force du vecteur bleu.
Hugo, le plus jeune tire la locomotive dans la direction et avec la force du vecteur rouge.
La locomotive va se déplacer selon le vecteur vert.
Différence entre deux vecteurs
Pour soustraire deux vecteurs on ajoute au premier l’opposé du second.
A l’extrémité du vecteur on construit le vecteur opposé – au vecteur . Puis on joint l’origine du vecteur à l’extrémité du vecteur –.
On procède de la même façon pour construire la différence des deux vecteurs par la méthode du parallélogramme.
A partir d’un point du plan, on construit le vecteur puis le vecteur opposé à .La différence est la diagonale du parallélogramme déterminé par les vecteurs et .
Relation de Chasles
Si les vecteurs sont représentés par deux lettres (A, origine et B, extrémité).Et si l’origine du second vecteur porte la même lettre que l’extrémité du premier, on peut écrire l’égalité ci-contre.
Inversement, soit un vecteur désigné par deux lettres A et C, soit un point B quelconque du plan. On peut écrire la formule ci-contre.
Entre A et C on introduit une lettre correspondant au point quelconque.
on double cette lettre et on sépare les deux lettres identiques par le signe +.
Cela fonctionne avec n’importe quel point du plan où qu’il soit.
Cette formule de Chasles fonctionne avec plusieurs vecteurs.
il suffit de les placer à la queue leu leu en respectant leur nomination telle qu’elle a été définie ci-dessus.
Un vecteur peut être considéré comme le somme de plusieurs vecteurs pourvu qu’on respecte la règle de la relation de Chasles.
Ainsi le vecteur vert si contre est la somme des vecteurs indiqués.
On constate que l’ordre des points n’a aucune importance pourvu qu’on respecte la règle de répétition de chacun des points.
Cette relation de Chasles appliquée dans un sens comme ci-dessus ou dans l’autre comme ci-contre est d’une grande importance pour le calcul vectoriel qu’il soit effectué avec ou sans figure.
Multiplication par un scalaire
Pour construire le vecteur 
qui doit être égal à 
, 3 fois le vecteur 
, à partir d’un point quelconque du plan, on mène une parallèle au vecteur . Puis à partir de ce point, on reporte, avec un compas, 3 fois le vecteur .
Les vecteurs et sont colinéaires.
On procède de la même façon avec les vecteurs et 
. Le nombre par lequel on multiplie le vecteur est négatif. Donc les vecteurs et seront dans des sens opposés.
Pour construire le vecteur 
, il faut “partager le vecteur en deux et en reporter la moitié à partir d’un point quelconque”. Pour être cohérent avec la définition des vecteurs, on a reporter selon un segment AB la norme du vecteur .On a partager ce segment en deux, AC=CB et on a reporter AC sur une parallèle à
Colinéarité de deux vecteurs
Deux vecteurs sont colinéaires, s’ils ont la même direction.
Ils n’ont pas forcément le même sens et la même norme (longueur).
Deux vecteurs et sont colinéaires s’il existe un réel k tel que 
.
Dans l’exemple ci contre 
donc et sont colinéaires.
Combinaison linéaire
Bien sûr on peut effectuer une combinaison de la somme de vecteurs et de la multiplication par un scalaire.
Soit le vecteur tel que
A partir d’un point quelconque du plan, on commence à construire le vecteur . Pour cela on construit une parallèle au vecteur passant par le point et à partir du point on reporte 3 fois le vecteur .
On construit ensuite le vecteur 
.
On mène une parallèle au vecteur passant par l’extrémité du vecteur .Puis à partir de cette extrémité, on reporte 2 fois le vecteur , mais dans son sens opposé.
On joint l’origine du vecteur avec l’extrémité du vecteur .
On aurait pu construire ce vecteur avec la méthode du parallélogramme (en bleu clair).
Composantes d'un vecteur
On a appris ce qu’étaient les coordonnées d’un point.
Voyons maintenant ce que sont les composantes d’un vecteur.
Dans un plan, il existe deux composantes d’un vecteur : une composante horizontale (en bleu)et une composante verticale (en vert).
La composante horizontale (en bleu) consiste au nombre de carreaux dont on se déplace horizontalement depuis l’origine du vecteur jusqu’à la projection orthogonale de son extrémité. Si on se déplace de gauche à droite la composante est positive 
et 
. Si on se déplace de droite à gauche elle est négative 
.
La composante verticale (en vert) est le nombre de carreau dont on se déplace verticalement. Si on se déplace de haut en bas, la composante est positive, et 
. si on se déplace de haut en bas, la composante est négative .
Lorsqu’il n’y a pas de déplacement vertical, le vecteur est horizontal, .
Lorsqu’il n’y a pas de déplacement horizontal, le vecteur est vertical, .
On écrit les composantes du vecteur selon la formule ci-contre.
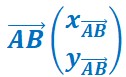
Dans un repère orthonormé (axes orthogonaux et unités égales sur les deux axes) , la composante horizontale (en bleu sur le croquis ci-contre) est sur l’axe des abscisse, l’axe des x.
La composante verticale (en vert sur le croquis) se situe sur l’axe des ordonnées, axe des y.
Mais cette fois elles sont exprimées à partir de l’origine O des deux axes.
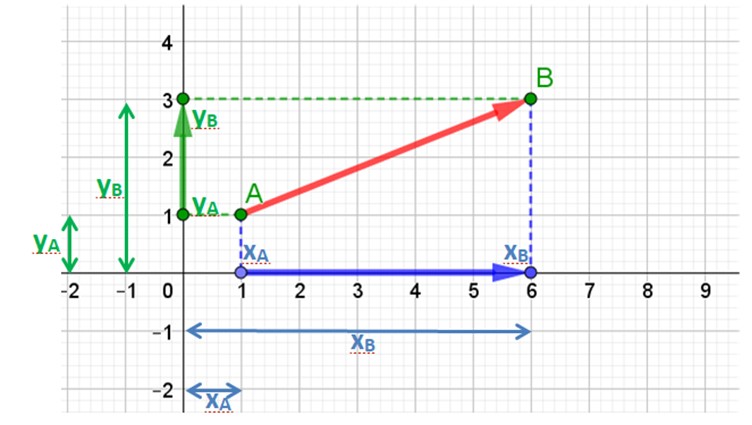
Les coordonnées du point A écrites en ligne sont : 
, ou écrites en colonne :
.
Les coordonnées du point B sont 
, 
.
On voit bien sur le croquis que la composante horizontale du vecteur est égale la longueur xB moins la longueur xA.
Donc la composante horizontale de est égale à l’abscisse de l’extrémité B du vecteur moins l’abscisse A de son origine.
Ainsi dans notre cas particulier, 
Donc :
Et on remarque qu’on se déplace de 5 unités vers la droite à partir de A puis de 2 unités vers le haut.
Coordonnées du milieu d'un segment
Puisqu’un vecteur n’a pas de localisation particulière dans le plan, il serait malvenu de dessiner le milieu d’un vecteur. Au mieux on pourrait parler du milieu d’un représentant d’un vecteur. Mais le milieu d’un segment est plus approprié.
Soit le segment AB et M son milieu.
Les coordonnées de A sont (xA;yA)
Les coordonnée de B sont (xB;yB)
Les coordonnées de M sont (xM;yM)
Si on prend l’abscisse des points A,B et M, nous constatons que d’après le graphique nous pouvons écrire : 
mais aussi 
Si on additionne membre à membre ces deux égalités nous obtenons l’équation 
.
Cela nous permet de trouver xM.
On procède de la même façon pour trouver yM, l’ordonnée du milieu M du segment AB.
Dans le cas particulier, les coordonnées de A et B sont d’près le graphique :
Nous en déduisons, d’près les deux formules, les coordonnées du point M :
Norme d'un vecteur
Soit le vecteur .
Il nous faut trouver la norme de ce vecteur. La norme, rappelons le est la longueur du vecteur.
Le triangle ABC est un triangle rectangle en C par construction dans le repère orthonormé. AB en est l’hypoténuse.
D’après le théorème de Pythagore, on peut écrire : 
En utilisant la formule donnant les composantes d’un vecteur en fonction des coordonnées de son extrémité et de son origine, on peut écrire :
Comme : 
Il ne reste plus qu’à prendre la racine carrée de tout cela:
Dans le cas particulier de la figure ci-contre où :
Il suffit de remplacer les lettres dans la formule par les chiffres appropriés :
Tout le reste n’est que calculs :
La norme du vecteur est égale à environ 8,94 unités du graphique. On ne sait pas si l’unité du graphique correspond à 1 cm ou autre.
Coordonnées dans une base
Rappelons que nous travaillons dans un repère orthonormé.
1
2
3
4
Jusqu’à présent le graphe avait une origine O et une unité sur l’axe des abscisses et une unité sur l’axe des ordonnées.
Parfois on nommait ce graphe (O;OI;OJ) sachant que OI et Oj valaient 1
A la place de OI et OJ on va désigner l’unité par deux vecteurs 
et 
à condition que ces deux vecteurs ne soient pas colinéaires. Ces deux vecteurs sont une base.Tout vecteur du plan pourra être exprimé par une combinaison linéaire avec cette base.
Soit un vecteur
Soit un vecteur tel que =
Ces deux vecteurs sont égaux.
1 nous connaissons les coordonnées de l’origine et de l’extrémité du vecteur .
2 A partir de ces coordonnées, nous calculons les composantes du vecteur .
Nous savons qu’un vecteur peut-être exprimé par une multiplication par un scalaire.
La composante horizontale de est égale à X fois le vecteur unitaire.
La composante verticale de est égale à Y fois le vecteur unitaire .
3 Le vecteur est égal à la somme des vecteurs 
et (par construction, et relation de Chasles).
4 d’où la formule.
Dans le cas particulier de la figure ci-contre :
1 coordonnées de A et B 
2 Composantes du vecteur 
3 
4 
Opérations autre façon
Addition de deux vecteurs.
1 
2
3
4
5
6
7
Nous allons voir comment additionner deux vecteurs très simplement.
Dans un premier temps on calculera avec des lettres pour avoir un point de vue général, puis on prendra le cas particulier du graphique ci-contre comme exemple.
1
On connaît les coordonnées des origines et des extrémités des deux vecteurs.
2
On peut calculer à partir de ces coordonnées les composantes des vecteurs et .
3
On nomme ces composantes X et Y pour chaque vecteur.
La composante horizontale du vecteur est égale à X fois le vecteur unitaire .
La composante verticale du vecteur est égale à Y fois le vecteur unitaire .
Il es est de même du vecteur .
4
De ce fait on peut écrire les deux égalités de nos deux vecteurs en fonction de X, Y et des vecteurs unitaires des deux axes.
On obtient ainsi deux équations.
5
Pour effectuer la somme des deux vecteurs, on additionne membre à membre les deux équations.
6
On rassemble les termes en puis les termes en .
7 on factorise et nous obtenons les composantes du vecteur +.
Voyons l’exemple particulier.
1
2
3
4
5
6
Multiplication par un scalaire.
1
2
3
4
Dans la figure ci-contre les deux vecteurs 
et 
ont pour origine O. Donc, leurs composantes seront égales aux coordonnées de leur extrémité A et B.
1 on note ces composantes.
2 On note que le vecteur est égal à un certain nombre k de fois le vecteur .
3 On note selon la première façon.
4 on note selon la deuxième façon avec les vecteurs unitaires et
Pour le cas particulier du graphique ci-contre, les composantes des deux vecteurs sont : 
que l’on peut traduire avec les vecteurs unitaires :
Colinéarité de deux vecteurs
Théorème directe. Condition nécessaire.
1
2
3
4
5
6
1- Nous avons vu précédemment (9):
Deux vecteurs et sont colinéaires si et seulement s’il existe un réel k tel que 
.
2- Dans le graphique ci-contre, on dispose de 4 points A,B,C,D dont on connaît les coordonnées. A partir de ces 4 points, nous pouvons calculer les composantes des vecteurs et reliées par la relation 1.
3- On désigne par 
et 
les composantes du vecteur et par 
et 
les composantes du vecteur .
4- On note les relations liant les composantes des vecteurs.
5- On multiplie la première composante du vecteur par la deuxième composante du vecteur , puis on soustrait le produit de la deuxième composante du vecteur par la première composante du vecteur .
6 Or d’après 4 
et 
Nous en déduisons que pour deux vecteurs colinéaires 
L’expression 
est appelée déterminant des deux vecteurs.
Elle est difficile à priori à calculer car il faut se souvenir dans l’opération de l’ordre des composantes, ce qui n’est pas une mince affaire.
Mais si nous disposons les composantes de chacun des vecteurs en colonne, nous avons un moyen technique pour le calculer.
En fait c’est au départ c’est un produit en croix. 
On calcule 
Puis on fait la différence des deux :
C’est le déterminant des deux vecteurs.
Si ce déterminant est égal à 0, les deux vecteurs sont colinéaires, sinon ils ne le sont pas.
Dans l’exemple donné sur le graphique, les vecteurs et sont colinéaires.
Donc 
.
Ecrivons côte à côte les composantes des deux vecteurs déduites de la ligne précédente. 
, Calculons le déterminant des deux vecteurs :
Il est bien égal à 0
Réciproque. Condition suffisante.
1
2
3
4
5
6
7
8
Soit les composantes et d’un vecteur et les composante et d’un vecteur .
1-Par hypothèse le déterminant de ces deux vecteurs est égal à 0
2- Le déterminant des deux vecteurs est égal à 0
3- On fait passer 
dans le second membre en changeant bien sûr son signe.
4- on divise par s’il n’est pas nul
5- on divise par s’il n’est pas nul, on obtient l’égalité de deux rapports, de deux fractions. Soit 
la valeur de ces deux fractions.
6- Chacune des fractions est égale à
7- On effectue pour chacune le produit en croix. On obtient deux égalités traduisant le fait que chacune des composantes du vecteur est égale à chacune des composantes du vecteur multipliée par .
Puisque 
les vecteurs et sont colinéaires.
Condition nécessaire et suffisante.
Vecteur directeur d'une droite
Un vecteur directeur de la droite passant par A et B est un vecteur qui est colinéaire au vecteur .
Si l’équation de la droite est une équation réduite :
les composantes d’un vecteur directeur sont sont :
Si l’équation de la droite est une équation cartésienne, 
, les composantes d’un vecteur directeur sont 
Dans l’exemple ci-contre, si on parle en terme de fonctions la droite est une fonction affine de la forme
La droite passe par les points A et B. Cette droite a pour taux d’accroissement : 
soit :
Ce taux d’accroissement est aussi le coefficient directeur a de la droite, encore appelé pente de la droite. (Rappelons qu’il est égal à la tangente de l’angle que fait la droite avec l’axe des abscisse, avec l’horizontale). a=2
de plus la droite passe par le point de coordonnées :
b=-2
L’équation réduite de la droite est donc ;
Un vecteur directeur est bien 
A partir de l’équation réduite on peut écrire l’équation cartésienne, il suffit de tout faire passer dans le premier membre sachant qu’il restera évidemment 0 dans le second. 
Et on constate en appliquant la seconde formule qu’un vecteur directeur l’un ou l’autre de ceux-ci:
ou encore :
Pourvu qu’ils soient tous colinéaires. Bien sûr on choisira toujours le plus simple.
Produit vectoriel
Produit de deux vecteurs 
Soit deux vecteurs 
et 
, le produit vectoriel de ces deux vecteurs est un vecteur 
:
– perpendiculaire à la fois à et à
– dont le sens est tel que le trièdre 
ou 
soit dans le sens direct ( Pour trouver son sens on peut utiliser la règle du tire bouchon.)
– et dont la norme est égal au produit des normes des deux vecteurs multiplié par le sinus de l’angle formé par les deux vecteurs.
Cette norme du vecteur est égale à l’aire du parallélograme ABDC formé par les deux vecteurs.
Calculons l’aire du parallélogramme ABDC Elle est égale au côté AC multiplié par la hauteur BH. 
Exprimons BH en fonction de AB et de l’angle α.
Le triangle ABH est un triangle rectangle en H et le sinus de l’angle α est égal au côté opposé divisé par l’hypoténuse 
. On en déduit AH :
.
Il suffit de remplacer BH par cette valeur dans l’expression de l’aire du parallélogramme. 
. Et nous trouvons bien que l’aire du parallélogramme ABDC est bien égale à la norme du vecteur AE.
Règle du tire-bouchon.
Il existe aussi la règle de la main droite. Mais elle est difficile à appliquer car il faut se tordre la main et le pouce.
La règle du tire-bouchon me semble plus parlante. Elle coule de source si je puis dire. De plus, il est agréable de l’expérimenter
Expression analytique du produit vectoriel
Méthode pour trouver les coordonnées du vecteur produit.
Pour trouver son abscisse :
Pour trouver son ordonnée :
Pour trouver sa cote :
Ci contre un repère dans l’espace.
L’axe en rouge est l’axe des abscisses ou axe des x de vecteur unitaire 
L’axe en vert est l’axe des ordonnées ou axe des y de vecteur unitaire 
L’axe en bleu est l’axe des cotes ou axe des z de vecteur
unitaire 
Dans l’espace un point quelconque M est repéré par trois nombres x,y,z. écrits en ligne ou en colonne. C’est comme un repérage dans le plan avec un chiffre supplémentaire. 
Le repère est directe si on applique la règle du tire-bouchon. On pose le tire-bouchon sur l’origine et on tourne de l’axe des x vers l’axe des y, alors l’axe des z correspond à l’avancement ou au recul du tire-bouchon.
Le repère ci-contre est direct
Les vecteurs et ont pour coordonnées :
que l’on peut écrire dela manière suivante :
et 
.
Effectuons bêtement le produit de ces deux vecteurs :
Il suffit de distribuer :
Sachant que les produits des vecteurs unité en utilisant la règle du tire-bouchon ont pour résultats :
on obtient après avoir éliminé les vecteur nuls :
on remplace les produits de vecteurs unitaires par leur résultat donné dans le tableau c-dessus :
On ordonne selon les vecteurs unitaires :
On factorise pour obtenir le résultat :
Ainsi :
Il est évident que ce travail est fastidieux et qu’il faudrait trouver une autre méthode pour calculer le produit de deux vecteurs.
La méthode est donnée dans la colonne de gauche.
Application numérique
Les trois points A,B,C ont pour coordonnées :
On veut faire le produit des vecteurs et : 
Calculons les trois composantes du vecteur 
Calculons les trois composantes du vecteur 
Nous pouvons écrire les deux vecteur de la manière suivante :
Et nous pouvons effectuer le produit :
On développe sachant qu’on peut laisser la troisième composante des deux vecteurs puisqu’elle est égale à 0.
En annulant ce qui doit l’être et en utilisant les produits des vecteurs unitaires : 
Ce n’est pas si fastidieux parce qu’on a pris un exemple simple.
Sinon, voyons l’autre procédure (voir ci-dessus) :
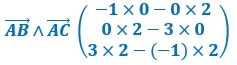
On obtient les composantes du vecteur 
. Pour trouver les coordonnées du point E :
