Les ondes mécaniques
- par gabriel
- dans phénomènes périodiques, Physique
- sur 12 octobre 2020

Onde sur l'eau
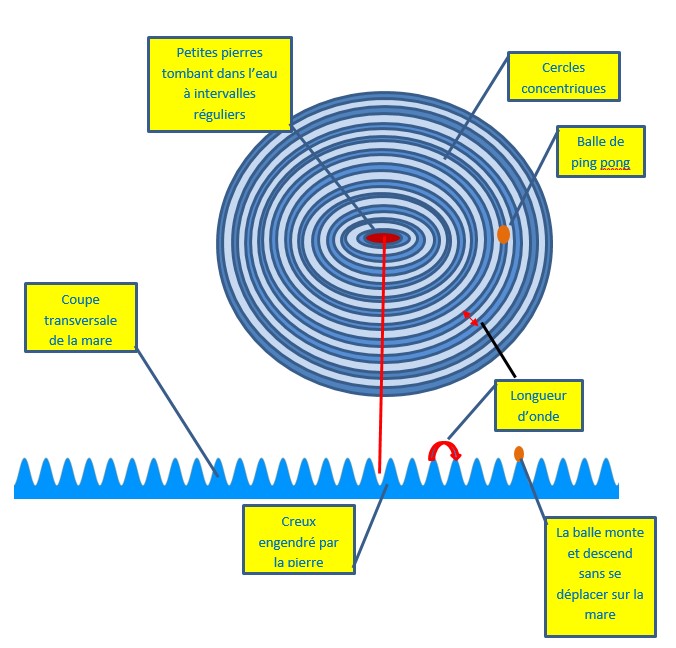
Je laisse tomber un petit caillou, je crée une perturbation de la surface de l’eau, des cercles concentriques se forment et disparaissent. A l’endroit où le caillou tombe dans l’eau, l’eau se creuse, mais aussitôt elle remonte.
Je laisse tomber plusieurs petits cailloux au même endroit à la surface de l’eau, à intervalles réguliers, j’entretiens la perturbation, des cercles concentriques se créent et restent visibles tant que la perturbation est entretenu par les petits cailloux qui tombent.
Les cercles concentriques se déplacent pas. Un cercle engendre à côté de lui une perturbation qui lui même engendre une perturbation et ainsi de suite.
Les cercles sont espacés régulièrement de la même distance.
Ces cercles sont une succession régulière de creux et de bosses.
Il n’y a pas de déplacement de matière. L’eau sous la balle de ping-pong est toujours la même. La balle monte et descend sans se déplacer à la surface de la marre.
On appelle longueur d’onde la distance entre deux bosses, ou la distance entre deux creux, c’est la même.
Je laisse tomber un petit caillou dans une mare.
Ca fait des « ronds dans l’eau » comme le chanterai Françoise Hardy.
Un petit rond apparaît à l’endroit où la pierre est tombée. Il disparaît et aussi tôt un rond plus grand apparaît (son centre est l’endroit où la pierre est tombée et le rayon plus grand que le premier rond.
Ce deuxième rond disparaît à son tour pour laisser place à un troisième rond et ainsi de suite de proche en proche. Les nouveaux ronds sont plus grands que les précédents. Essaie de faire l’expérience dans une bassine d’eau, une piscine, une mare…
Je laisse tomber une succession de petits cailloux à intervalles réguliers.
Le premier petit caillou tombe à la surface de l’eau qui se creuse à cet endroit. Il produit un petit rond qui va se propager comme nous l’avons vu ci-dessus.
Je lâche un deuxième petit caillou qui produit un petit rond. Ce nouveau petit rond va se propager en s’agrandissant.
Je lâche un troisième petit caillou qui va produire un nouveau petit rond qui va se propager.
Ainsi en lâchant les petits cailloux à intervalles réguliers j’entretiens la perturbation qu’ils créent à la surface de l’eau au point de contact avec la surface.
Pour en créer d’une façon continue, je dois laisser tomber des petits cailloux identiques à intervalles réguliers. J’obtiens ainsi une mare ridée par les cercles concentriques. C’est ça une onde.
Elle se propage à la surface de l’au dans toutes les directions.
Si, avec un masque de plongée je regarde ce qui se passe à la surface de l’eau, je vois une succession régulière de bosses et de creux.
Tout en continuant à lâcher les petits cailloux à intervalles réguliers. Je place une balle de ping-pong sur un cercle. Je m’aperçois que la balle reste au même endroit et ne fait que monter et descendre.
La distance entre deux crètes ou deux creux s’appelle longueur d’onde et se mesure en mètres.
Propagation d'une perturbation
Une onde mécanique est une perturbation qui se propage dans un milieu matériel : air, eau…
Une onde mécanique ne peut pas se propager dans le vide.
Prenons l’exemple d’une corde. Avec ma main je soulève brusquement son extrémité pis je reviens à ma position initiale. Je crée ainsi une perturbation sur l’extrémité de cette corde. Cette perturbation va se transmettre de proche en proche tout au long de la corde pour s’anéantir à l’autre bout. Si je ne recommence pas à soulever la corde avec ma main elle reprendra sa position d’équilibre rectiligne.
.




Si je recommence à bouger ma main vers le haut, une autre perturbation se crée et va se déplacer à nouveau.
Seule, la perturbation se déplace, et non de petits morceaux de corde.
La perturbation de départ est un soulèvement de la corde. C’est ce soulèvement de corde qui va se déplacer.
Si je recommence à déplacer ma main de bas en haut régulièrement, j’aurai une perturbation qui se créera régulièrement et qui se déplacera.
Et j’aurai une succession de perturbations qui se déplacerons à la queue leu leu.
La distance entre deux sommets ou entre deux creux est toujours la même, c’est la longueur d’onde dont l’unité de mesure est le mètre. 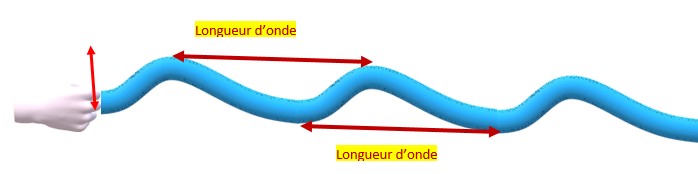
Que ce soit dans le cas de l’eau ou le cas de la corde, on a
Le facteur temps :
Au départ une perturbation régulière, une vibration, une pulsation qui correspond à une certain nombre de gouttes d’eau qui tombent par seconde et un certain nombre d’allers et retours par seconde de la main.
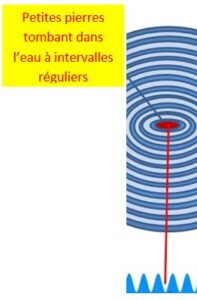

Le facteur espace :
La perturbation, la pulsation ou la vibration engendre à la surface de l’eau ou tout au long de la corde des ondulations qui sont des déplacements de la perturbation dans chacun de ces milieux.
![]()

A la source de la perturbation
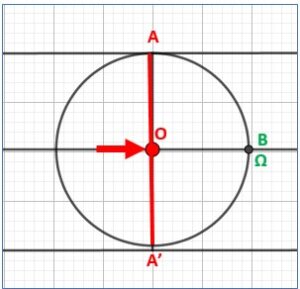

Imaginons que ma main, représentée par la flèche rouge, entraîne la corde entre les points A et A’ et qu’elle fasse 4 allers retours en 1 seconde : OA, AA’, A’0 4 fois.
Ce nombre d’allers et retours en 1 second est appelé fréquence et se mesure en hertz. Son symbole est f mais il fut ν (nu) autrefois.
On définit aussi la période T qui est le temps mis par ma main pour faire un aller et retour et qui se mesure bien sûr en seconde.
Si ma main fait 4 allers et retours en 1 seconde, elle mettra 1 divisé par 4 secondes pour faire un aller et retour, soit 0,25 s.
Imaginons maintenant un cercle dont le diamètre est le segment AA’. On considère que son rayon OA est égal à 1 unité. On notera que OA’ est égal à -1. Ainsi ma main va faire des allers et retours entre 1 et -1 en passant par O.
Sur le cercle un point B baladeur se déplace en même temps que ma main à partir de Ω qui sera l’origine du cercle. Ainsi ΩB détermine un arc de cercle égal à l’angle ΩOB mesuré en radian. Ici l’arc ΩB et l’angle ΩOB sont égaux à 0 radian.
Si ma main monte vers A, le point B, la suivant va se rapprocher de A tout en restant sur le cercle.
Ma main est immobile en O 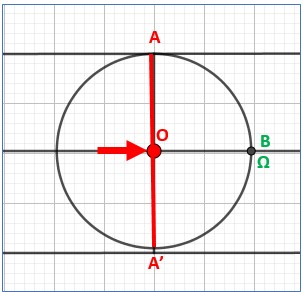
ΩMa main se trouve immobile en O.
Le point B baladeur est en Ω, à l’origine des arcs sur le cercle.
Ma mainte monte de O à A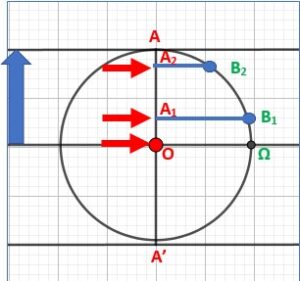
Ma main monte vers A.
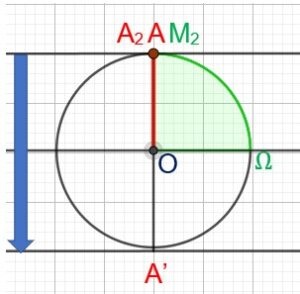
Elle passe par A1 et A2.
En même temps le point B se déplace sur le cercle en passant par B1 et B2.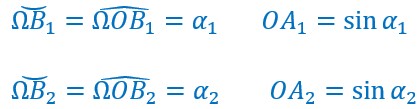
Ma main descend de A à A’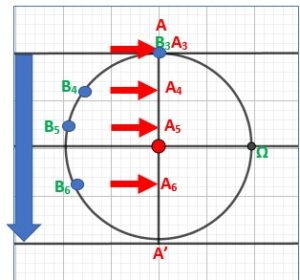
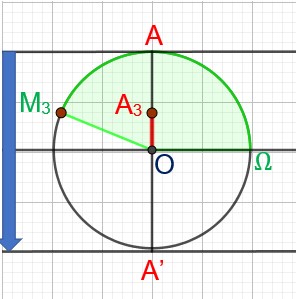
Ma main, Arrivée en A ou A3 descend jusqu’à A’.
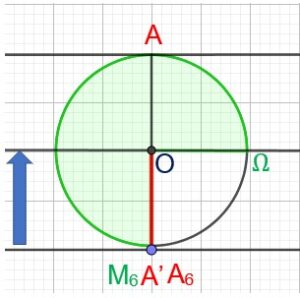
Elle passe par A3,A4,A5,A6, pour arriver en A’.
Sur le cercle le point B continue sa course depuis B3 en passant par B4,B5,B6. Il va se confondre avec A’.
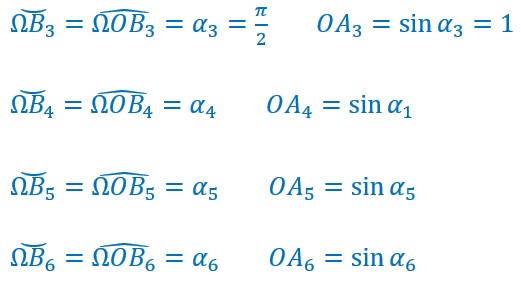
Ma main monte de A’ à O
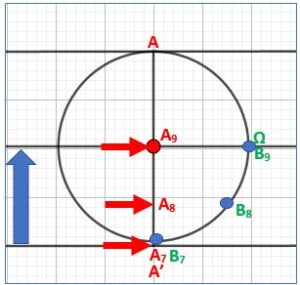
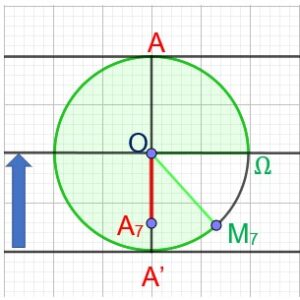
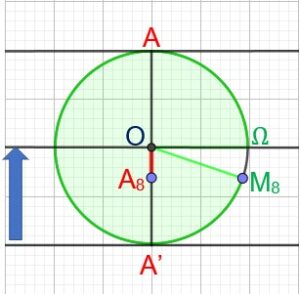
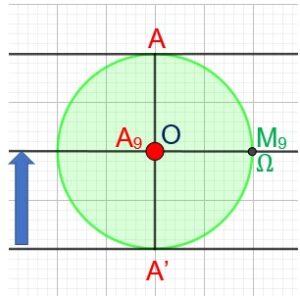
Ma main arrivée en A’ ou A7 monte jusqu’à O, A9 en passant par A8.
Le point B passe par B7, B8 pour arriver en Ω ou B9.
Ainsi ma main a effectué un aller et retour entraînant la corde.
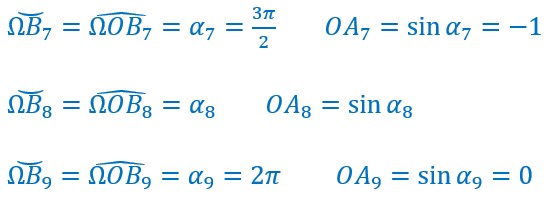
Le temps d’un aller retour de ma main, c’est-à-dire le temps d’une période T, ou encore le temps pour le point A de faire le trajet OAA’O, le point B part de Ω, fait le tour complet sur le cercle pour revenir en Ω.Le point B parcours un angle de 2π radians pendant que le point A parcours QAA’O en T secondes.
On peut ainsi définir la vitesse du point B sur le cercle appelée pulsation et dont le symbole est ω (oméga minuscule).C’est une vitesse angulaire.
dans ce cas la vitesse angulaire ω est constante, elle ne varie pas.![]()
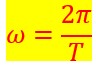
![]()
Mais la vitesse du point A, elle varie constamment entre A et A’. Elle est maximum au point O, mais elle diminue progressivement en s’approchant de A ou A’ pour augmenter progressivement lorsqu’il s’éloigne de A ou A’. On peut penser à un nageur effectuant des longueurs de bassin qui est bien obligé de ralentir en approchant des bords de la piscine. Il augmente sa vitesse après avoir fait demi-tour. Au moment où il atteint le bord, sa vitesse est nulle. Il en est de même du point A arrivant en A ou A’. Sa vitesse est nulle.
Bien sûr le cercle sur lequel se déplace le point B n’existe pas. Le point B n’existe pas.
Ils ne servent qu’à traduire le fait que les élongations OA1, OA2, OA3.……..sont équivalentes à des sinus d’angles successifs.
Animation
Cliquer sur la petite flèche en bas à gauche pour démarrer ou arrêter à volonté l’animation.
Le point A qui se déplace entre A1 et A2 représente l’extrémité de la corde entraînée par ma main.
Le point B fictif, se déplace sur le cercle fictif avec une vitesse angulaire ω constante.
Le point B est repéré par l’angle ![]() mesuré ici en radian.
mesuré ici en radian.
L’élongation, c’est-à-dire la position de A par rapport à O sur A1A2 est égale à : ![]() .
.
OA varie entre 1 et -1.
B circule entre 0 et 2π radians, donc entre 0 et 6.28 radians.
Cas concret
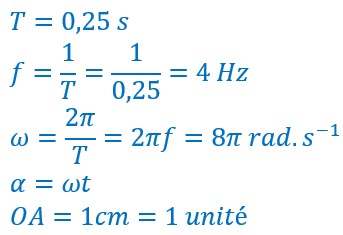
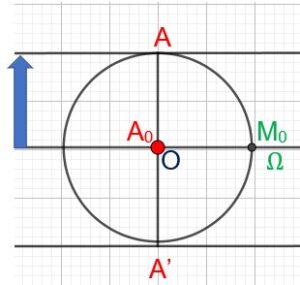
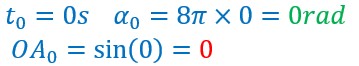
Soit une vibration commençant en O et d’un aller et retour en un quart de seconde. La période T est donc de 0, 25 seconde.
Sa fréquence qui est l’inverse de la période sera de 4 Hz, soit 4 allers et retours en une seconde.
Pendant que le point A exécute son aller et retour à partir de O, le point M effectue un tour complet sur le cercle soit 2π radians.
Il parcourt 2π (6,28) radians en 0,25 seconde.
Sa vitesse angulaire ω (nombre de radians en une seconde) sera donc égale à l’angle parcouru divisé par le temps mis à le parcourir soit 8π (25,12) radians.
De plus, OA = 1 unité, Ici ce sera 1 cm.
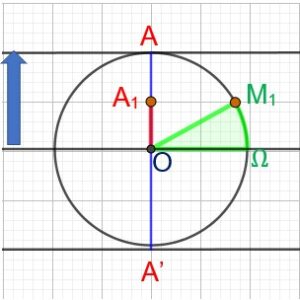
En fonction du temps t, l’angle α parcouru par M est α=ωt (vitesse angulaire multipliée par le temps)
Pour des temps t0,t1,t2…….t9, on a calculé l’angle parcouru et l’élongation.
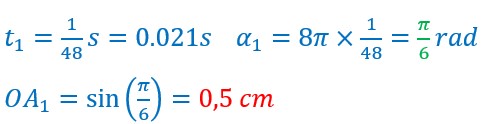 p
p
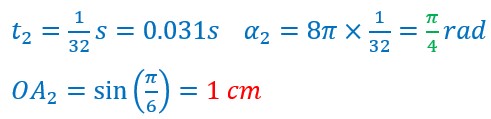

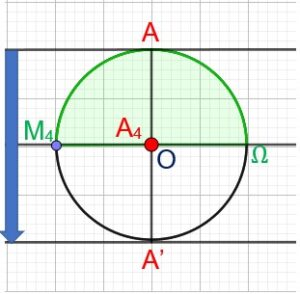
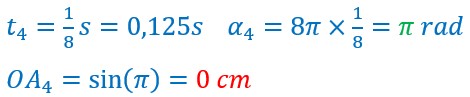
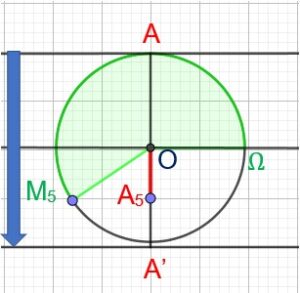
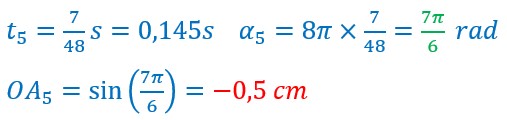
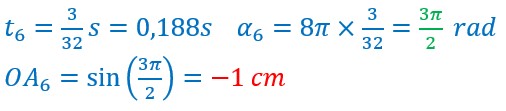
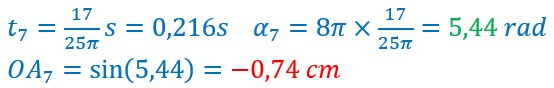
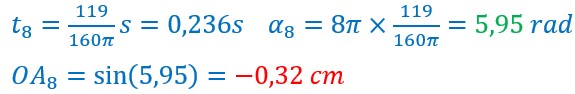
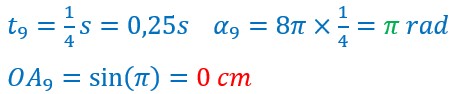
transmission de la perturbation
Ci-contre sont représentés plusieurs points sur la corde, M,N,P….Les points suivants n’ont pas été nommés pour ne as surcharger la figure. Le point M est au début de la corde qui est actionnée par ma main en un mouvement de va et vient à partir de 0 entre les ordonnée 1 et -1.
Le point N qui est un peu plus loin sur la corde va subir la perturbation avec un certain retard, puis le point P et tous les autres points les uns après les autres.
Ainsi toute la corde va subir la perturbation successivement en chacun de ses points.
Notons que les points ne se déplacent pas selon l’axe horizontale, mais uniquement sur l’axe verticale selon un mouvement de va et vient.
C’est ce qui se produit pour un ballon laissé sur une vague.
Cliquer sur la petite flèche entourée en bas à gauche vers le 2. On peut aussi faire glisser le curseur des angles en haut à gauche.
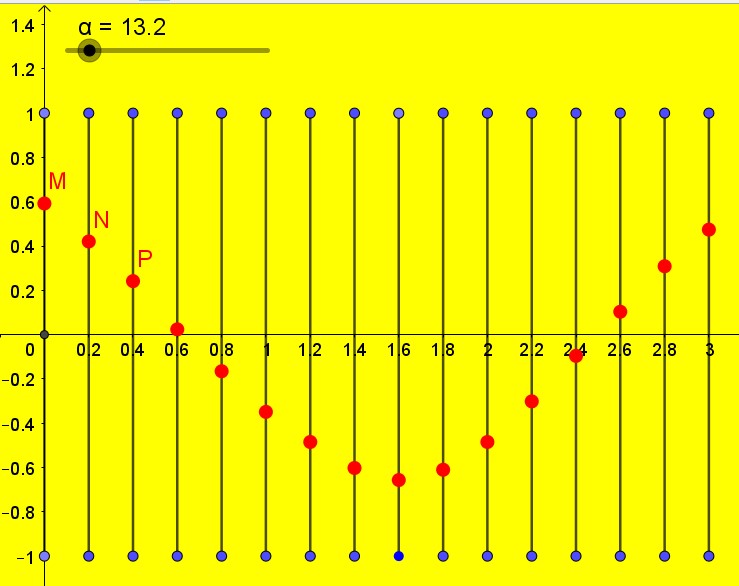

Voyons la situation du point M sur la figure.
Rappelons qu’il oscille entre 1 et -1, comme la valeur du sinus d’un angle.
Actuellement il est en position 0,6 qui peut-être considérée comme le sinus d’un angle de 0,64 radians (environ 37°). Il met environ 0,7 seconde pour parcourir 0,6.
Dans le tableau ci-dessous les valeurs sont résumées pour les position de M correspondant à 0,6 ; 0,8 ;0 (après un aller et retour).

Le seul chiffre constant est la vitesse angulaire.
En partant de la vitesse angulaire ω, en la multipliant par le temps t on obtient un angle α, puis son sinus et ainsi la position du point M au temps t . Si on appelle y cette position, on peut écrire ainsi l’équation : ![]()

ϖVoyons ce qui se passe pour le point N.
Manifestement il est en retard par rapport au point M. Il atteindra la position du point M (0,6) plus tard. Il y a un décalage entre le mouvement du point N et celui du point M.
Pendant que M est en 0,6, N est en 0,4 environ. Soit un décalage de 0,2. Ce décalage correspond à un sinus sur l’axe des ordonnées. Ce sinus correspond à un angle de 0,2 radian (11,5 degrés).
Au niveau des sinus il y a un décalage de 0,2 et au niveau des angles, il y a un décalage de 0,2 radians. car l’angle dont le sinus est 0,2 est un angle de 0,2 radians environ. Les valeurs sont les mêmes mais l’une est le sinus 0,2 et l’autre l’angle 0,2 radians.
Ainsi le décalage (déphasage) entre N et M sur l’axe des ordonnées est donc : ![]()
L’angle dont le sinus est 06 est un angle de 0,64 radians
L’angle dont le sinus est 0,2 est un angle de 0,2 radians. ![]()
Or cet angle de 0,64 radians est parcouru en t= 0,7 seconde à une vitesse angulaire de ω=0,9 radians par seconde. ![]()
5 réponses
Article writing is also a fun, if you know then you can write or else it is difficult to write. Misty Brok Hermia
My brother recommended I might like this web site.
He was entirely right. This post truly made my day.
You can not imagine just how much time I had spent for
this info! Thanks!
Hmm it seems like your website ate my first
comment (it was super long) so I guess I’ll just sum it up what I submitted and say, I’m thoroughly enjoying your blog.
I as well am an aspiring blog writer but I’m still new to the whole thing.
Do you have any recommendations for first-time blog writers?
I’d definitely appreciate it.
Oui merci mais je ne parle que très difficilement l’anglais
Many a true word is spoken in jest.