Proportionnalité, proportions, pourcentages, ratio. 6-5-4-3
Proportionnalité
Deux grandeurs associées A et B sont proportionnelles si lorsque on multiplie la valeur de A par un nombre n, alors la valeur de B est aussi multipliée par le même nombre n.
On multiplie par un même nombre les grandeurs de la première ligne et les grandeurs de la deuxième ligne.
Un maraîcher vend ses pommes 5 euros le kilo.
Pour éviter de compter, il élabore un tableau (ci-contre). Dans la première ligne de ce tableau, il note la masse de pomme en kilogrammes. Dans la seconde ligne, il note le prix en euros.
Ainsi il existe bien deux grandeurs associées ; la masse des pommes d’une part et leur prix d’autre part.
Si je considère les grandeurs surlignées en jaune :
dans la première ligne je multiplie la première grandeur 1par 2 , je passe de 1 à 2;
dans la seconde ligne je multiplie aussi la première grandeur 5 par 2 : je passe de 5 à 10.
Si je considère les valeurs surlignées en vert :
dans la première ligne je multiplie la première valeur 3 par 3, je passe de 3 à 9;
dans la seconde ligne je multiplie aussi la première grandeur 15 par 3, je passe de 15 à 45.
Deux séries de nombres A et B sont proportionnelles si on multiplie tous les nombres de la première série A par un même nombre, appelé coefficient.
Pour obtenir les nombres de la deuxième série B (deuxième ligne) on multiplie chaque nombre de la première série A (première ligne) par un même nombre.
Pour obtenir les nombres de la deuxième série B, on multiplie tous les nombres de la série A par un même nombre, ici 5 qui est le prix de 1 kilogramme de pommes.
S j’achète 1 kilogramme de pommes, je vais payer 5 Euros.
Si j’achète 2 kilogramme de pommes, je vais payer 2 x 5= 10 Euros
SI j’achète 3 kilogrammes de pommes, je vais payer 3 x 5= 15 Euros
———————————————————————————————
Si j’achète 9 kilogrammes de pommes, je vais payer 9 x 5 Euros.
Et ainsi de suite, je peux continuer le tableau.
Il suffira de multiplier la première ligne du tableau par 5 pour obtenir la deuxième ligne.
Bien sûr on peut éventuellement partir de la deuxième ligne pour aboutir à la première ligne. Dans ce cas on divise tous les nombres de la deuxième ligne par 5 pour obtenir les nombres de la première. Ou bien on les multiplie par 1 cinquième ce qui revient au même.
On donne cette fois le prix payé pour trouver la masse de pommes achetée.
Si j’ai payé 15 euros, j’ai donc acheté 3 kilogrammes de pommes.
SI j’ai payé 45 euros, j’ai donc acheté 9 euros de pommes .
Représentation graphique
Grandeurs proportionnelles.
Une situation proportionnelle ou un tableau de proportionnalité est représenté graphiquement par une droite passant par l’origine.
Soit un carré dont on connais la longueur du côté et dont on veut calculer le périmètre, 
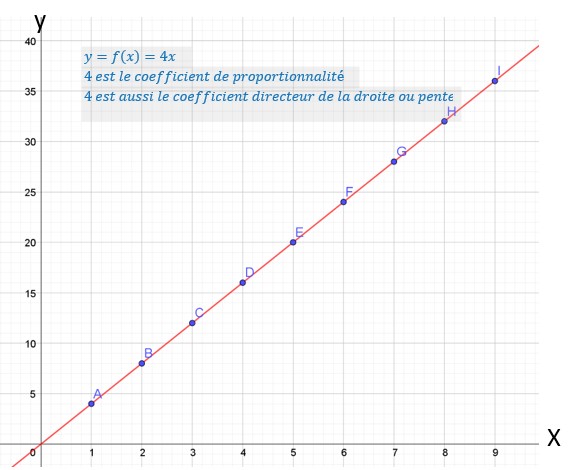
C’est une fonction linéaire du type :
Grandeurs non proportionnelles .
Si la représentation graphique de deux grandeurs associées n’est pas une droite passant par l’origine alors ces deux grandeurs ne sont pas proportionnelles.
Soit un carré dont on connait la longueur du côté et dont on veut calculer l’aire . 
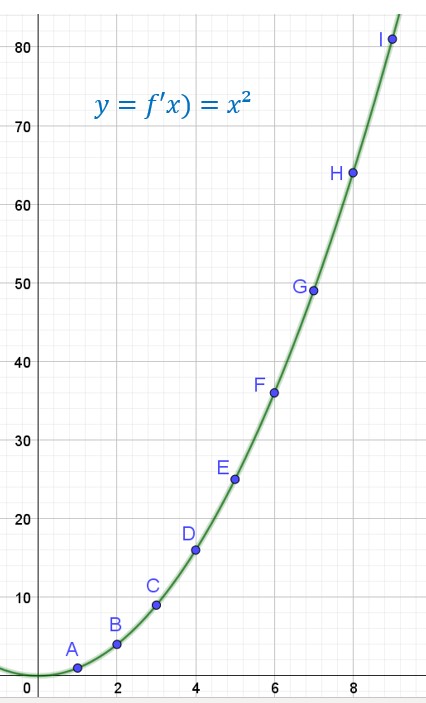
Ce n’est pas une fonction linéaire.
Propriétés des proportions
Une proportion est l’égalité de deux rapports, de deux fractions.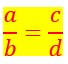
IL est intéressant de repérer en les nommant chacun des chiffres de la proportion.
Ainsi on appelle extrêmes les chiffres en rouge a et d situés à son extrémité.
.
Et on appelle moyens les chiffres en rouge b et c situés au milieu de la proportion.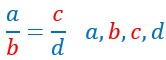
Les deux fractions, les deux rapports ci-dessous sont égaux. Ils constituent une proportion.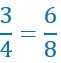
3 et 8 sont les extrêmes de cette proportion.
4 et 6 sont les moyens de cette proportion.
Dans une proportion, le produit des extrêmes est égal au produit des moyens. On appelle cette égalité le produit en croix. 
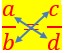
Dans la proportion ci-dessous, il est évident que le produit des extrêmes 3 fois 8 est égal au produit des moyens 4 fois 6. 
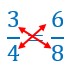
Dans une proportion, on peut intervertir les extrêmes pour obtenir une autre proportion. 
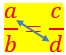
Les deux proportions celle de départ et celle d’arrivée après interversion des extrêmes n’ont pas la même valeur.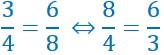 
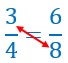
Dans une proportion, on peut intervertir les moyens pour obtenir une autre proportion.
Les deux proportions, celle du départ et celle de l’arrivée après interversion des moyens n’ont pas la même valeur.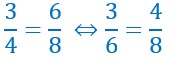 
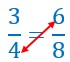
Si deux rapports forment une proportion (les deux fractions sont égales), on obtient un rapport égal aux deux premiers en prenant pour numérateur la somme ou la différence des numérateurs et pour dénominateur la somme ou la différence des dénominateurs.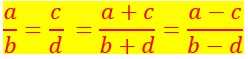 
Cette propriété est vraie avec une suite de rapports égaux.
Mieux :
Deux rapports sont égaux et forment donc une proportion.
On multiplie le numérateur et le dénominateur du premier rapport par un même nombre n.
On multiplie le numérateur du deuxième rapport par un même nombre m.
On additionne les numérateurs et les dénominateurs de ces deux nouveaux rapports.
On obtient un rapport égal aux deux premiers. 
On a effectué une combinaison linéaire des deux numérateurs puis des deux dénominateurs avec les mêmes coefficients.
Voyons ce que cela donne dans un cas concret :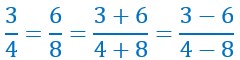
Avec trois rapports :
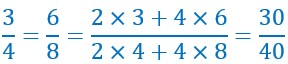
Cette propriété est très utilisée dans les problèmes de partage.
On obtient une nouvelle proportion si on ajoute ( ou soustrait ) le dénominateur au numérateur de chaque rapport.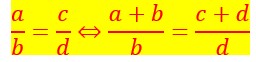
Exemple :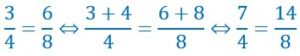
On obtient une nouvelle proportion si on ajoute (ou soustrait) le numérateur au dénominateur de chaque rapport. 
Exemple :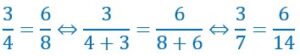
Ajoutez votre titre ici
Pourcentages
Un pourcentage traduit une situation de proportionnalité.
Mais le dénominateur d’un rapport de la proportion est 100.
En effet parler de c% revient à écrire :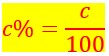 
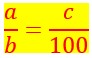
A quoi ça sert ?
Il est difficile de comparer deux fractions qui n’ont pas le même dénominateur. Pour les comparer, il faut réduire au même dénominateur.
Dire que 
des élèves de la classe de troisième A étudient l’allemand et que 
des élèves de la classe de troisième B étudient l’allemand ne nous permet pas de comparer. Il faut pour cela réduire les deux fractions en douzièmes. Ainsi 
des élèves de la classe A contre 
des élèves de la classe B étudient l’allemand. On voit ainsi que Proportionnellement, il y a plus d’élèves qui apprennent l’allemand dans la classe A.
Il serait intéressant que la comparaison puisse être universelle, c’est-à-dire puisse toujours se faire rapidement, immédiatement quelle que soit la quantité envisagée. Ainsi, au lieu de réduire au même dénominateur 12, on réduit toujours au même dénominateur 100.
75 % des élèves d’une classe étudient l’allemand en première langue signifie que 75 élèves sur 100 élèves étudient l’allemand. 
Mais si on simplifie la fraction 
on aboutit à la fraction irréductible .
Ainsi, on peut écrire :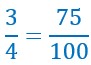
Dire que les ou dire que ou encore 75% des élèves étudient l’allemand est équivalent, c’est la même chose.
Classe de troisième A : des élèves apprennent l’allemand. Soit 75%
Classe de troisième B ; des élèves apprennent l’allemand. Soit 66,6%
Classe de troisième C : 
des élèves apprennent l’allemand. Soit 40%
Appliquer un pourcentage à une quantité
Soit x les p% de A.
Première méthode, la plus simple
Prendre les p% d’une quantité A revient à prendre les 
de cette quantité A et donc de multiplier par A.
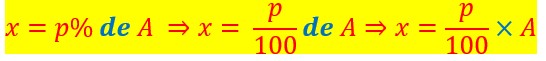
Deuxième méthode, avec les proportions.
p est une quantité partielle par rapport à 100 qui est une quantité totale
x est une quantité partielle par rapport à A qui est la quantité totale réelle.
Troisième méthode : coefficient multiplicateur :
Dans la première méthode on multiplie la quantité A par .
Il suffirait de multiplier A par la résultat de la division de p par 100 qui est facile à effectuer. Soit m ce résultat qu’on appellera coefficient multiplicateur.
Tu vas manger 25% de cette belle tarte tatin ayant une masse de 500 g. Quelle masse de la tarte vas-tu manger ?
Première méthode, la plus simple
Soit x cette masse.
Tu as mangé x= 25% de 500 g
Tu as mangé x= 
de 500 g.
Tu as donc mangé 
grammes de tartes.
Pour votre santé, évitez de grignoter entre les repas : www.mangerbouger.f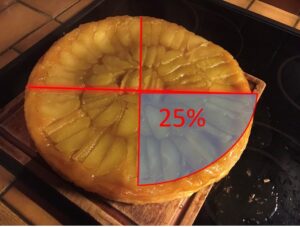
Deuxième méthode : avec les proportions.
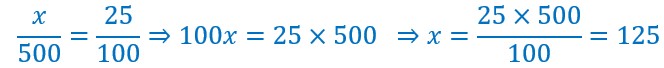
Troisième méthode : le coefficient multiplicateur.
On sait que :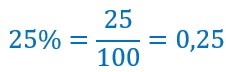
Ce résultat est le coefficient multiplicateur.
Il suffit de multiplier la masse totale de la tarte par ce coefficient multiplicateur pour trouver la masse de tarte que tu as mangé. 
Calculer un pourcentage dans une quantité
Il s’agit de calculer le pourcentage x d’une quantité A contenue dans une quantité B.
Première méthode :
Si on divise A par B, on obtient la quantité de A contenue dans une unité de B. Comme on veut la quantité de A contenue dans 100 quantités de B, il suffit de multiplier le résultat obtenu par 100. 
Si A est plus grand que B, alors x sera plus grand que 100.
Deuxième méthode :
On place les valeurs judicieusement dans un tableau de proportion. Il ne faut pas se tromper. 
On calcule avec les proportions. On peut passer directement à la formule ci-dessous avec l’habitude.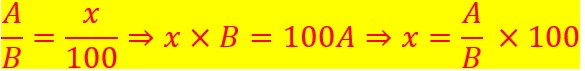 
Mettre de l’eau dans son vin.
Dans un verre de 20 cl, je verse 4 cl de vin puis, sacrilège, je le remplis avec de l’eau. Quel pourcentage de vin ai-je dans mon verre?
Première méthode toute simple :
J’ai mis 4 cl sur 20 cl au total
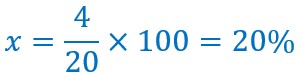
Deuxième méthode :
Augmentation ou diminution
Calculer une quantité après une augmentation.
Soit une quantité A. On lui applique une augmentation de p%.
Quelle est sa nouvelle valeur B après cette augmentation?
Première méthode : on calcule d’abord le montant de l’augmentation :
On augmente A de p%, on prend donc les p% de A :
On ajoute l’augmentation à A :
Ce qui donne :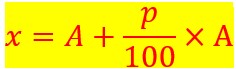
Deuxième méthode : On calcule avec un coefficient multiplicateur.
En partant de la formule précédente ; 
On factorise par A :
A l’intérieur de la parenthèse, on réduit au même dénominateur :
On ajoute les fractions :
On appelle coefficient multiplicateur la quantité : 
On obtient la formule :
Hugo avait 30 billes avant de jouer avec Moussa. Il en gagne 50% de ce qu’il avait. Combien en a-t-il maintenant.
première méthode :
On calcule l’augmentation du nombre de billes, c’est-à-dire, combien de billes il a gagné.
Il en a gagné 50% de ce qu’il avait soit 50% de 30 billes : 
Hugo a donc gagné 15 billes
Maintenant, il en a donc: 
Deuxième méthode : on calcule avec un coefficient multiplicateur :
En décomposant pour comprendre :
On met 30 en facteur : 
On calcule dans la parenthèse :
On obtient bien un coefficient multiplicateur: 1,5.
Pour aller plus vite il suffit de rajouter à 1 50%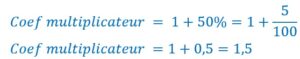
Il ne rest plus qu’à multiplier l’ancienne valeur par le coefficient multiplicateur pour obtenir la nouvelle valeur.
Ratio
Le ratio est une notion anglo saxonne qu’on utilise en économie, informatique, imprimerie, numérique, peinture, photographie, cinématographie, vidéo.
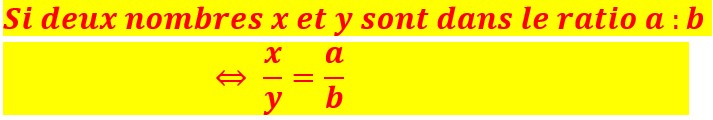
en effet :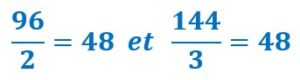 
de plus : 
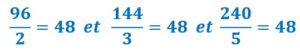
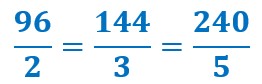
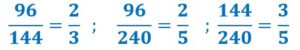
Exemples
En réglant le curseur rouge sur la valeur Sucettes=1,
je donne 3 sucettes à Blanche et 2 à Léonore.
En réglant le curseur rouge sur la valeur Sucettes=2,
je donne à nouveau 3 sucettes à Blanche et 2 à Léonore.
Pour finir, je règle le curseur rouge sur la valeur Sucettes=3,
je donne encore 3 sucettes à Blanche et 2 à Léonore.
Et je n’ai plus de sucettes à distribuer.
Finalement je vois que Blanche à 9 sucettes et Léonore 6.
Pour éviter ces manipulations qui ne seraient difficiles avec un grand nombre de sucettes, je peux raisonner ainsi:
Chaque fois je donne 3+2=5 sucettes.
Je distribue les sucettes en 15:5=3 fois.
Chaque fois Blanche a 3 sucettes donc en 3 fois :3 X 3=9 sucettes
Chaque fois Léonore a 2 sucettes donc en 3 fois 3 X 2=6 sucettes.
Pour éviter ce raisonnement je peux utiliser les définitions ci-dessus et les propriétés des proportions.
Si je désigne par Blanche (x) le nombre de sucettes que Blanche aura et par Léonore (y) le nombre de sucette que Léonore aura, je peux écrire et calculer :
Leur papy a retiré 40 billets de 20 euros à la banque pour les distribuer à ses 4 petits enfants Léonore, Blanche, Louison et Hugo selon le ratio 1:2:3:4.
Combien auront-ils de billets chacun ?
Papy doit distribuer 40 billets selon le ratio 1:2:3:4. A chaque tour de distribution il donnera 1 billet à Léonore, 2 billets à Blanche, 3 billets à Louison et 4 à Hugo soit 1+2+3+4=10 billets.
Ainsi à chaque tour il distribue 10 billets et comme il en a 40 à distribuer, il devra effectuer 4 tours de distribution.
Et au bout de 4 tours, Léonore aura 1 x 4 =4 billets,
Blanche en aura 2 x 4 = 8,
Louison en aura 3 x 4 =12
et Hugo 4 x 4=16.
Dans un premier temps, alors que Papy distribuera 1 billet à Léonore, il en distribuera 2 à Blanche, 3 à Louison et 4 à Hugo.
Pour cela je déplace le curseur billets sur 1
Il fait ensuite une autre distribution de la même façon Je déplace le curseur billets sur 2
Pour la troisième distribution, je déplace le curseur billets sur 3
Pour la quatrième distribution, je déplace le curseur billets sur 4
Et Papy a distribué tous ses billets.
Utilisons les définitions mathématiques du ratio et les propriétés des proportions :