La numération en base 2,3,4…,9 et 16
- par gabriel
- dans Calculs, Mathématiques
- sur 3 juillet 2022
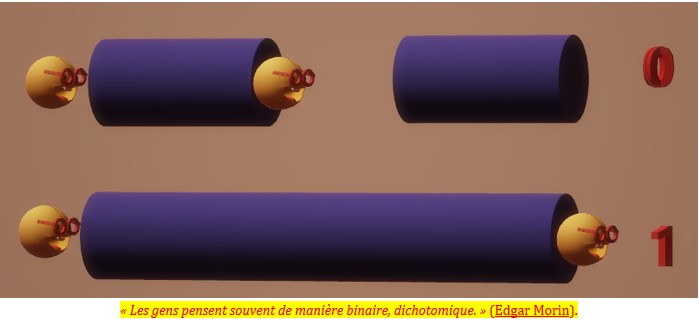
Base 2 ou binaire
En base deux je ne possède que deux chiffres pour compter, le zéro et le un, 0 et 1.
Et il n’existe pas de mots pour désigner les nombres écrits en base 2

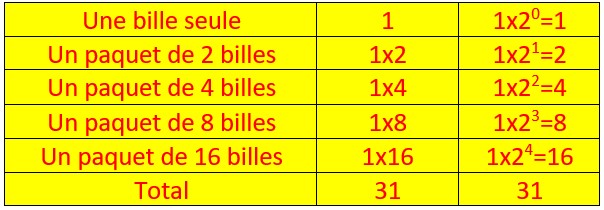
Voilà un certain nombre de billes de toutes les couleurs.
En base dix je regrouperais ces billes par paquets de dix.
En base deux, je vais les regrouper en paquets de deux billes.

J’obtiens ainsi quinze paquets de deux .
et il reste une bille grise toute seule.
Je vais regrouper les paquets de deux billes en paquet de deux.
Je vais obtenir des paquets de deux paquets de deux, soit des paquets de quatre.
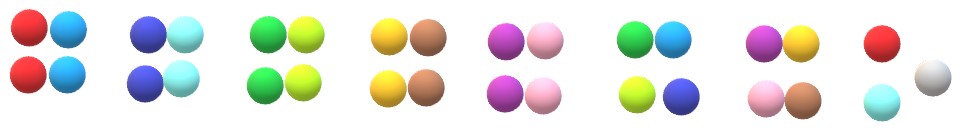
J’obtiens ainsi sept paquets de quatre.
Et il reste un paquet de deux et une bille toute seule.
Je vais regrouper les paquets de quatre en paquets de deux paquets de quatre, soit des paquets de huit.

J’obtiens trois paquets de huit billes.
Et il reste un paquet de quatre, un paquet de deux et une bille.
Je vais regrouper les paquets de huit en paquets de deux paquets de huit, soit des paquets de seize billes.

J’obtiens un paquet de seize billes.
Et il reste un paquet de huit, un paquet de quatre, un paquet de deux billes plus une biille toute seule.


Finalement j’ai :
une bille seule
un paquet de deux billes
un paquet de quatre billes
un paquet de huit billes
un paquet de seize billes.
Tout cela est résumé dans le tableau ci contre.
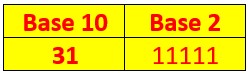
Si j’avais compté en base 10 c’est-à-dire en regroupant les billes par paquets de 10 et non pas par paquets de 2, j’aurais obtenu le nombre 31 comme indiqué dans le tableau ci-contre.
Le nombre 31, trente et un écrit en base 10 s’écrit 11111 en base 2 et il n’y a aucun vocabulaire pour le dénommer. On dit simplement un,un,un,un,un.
Conversion d’un nombre de la base 2 à la base 10.
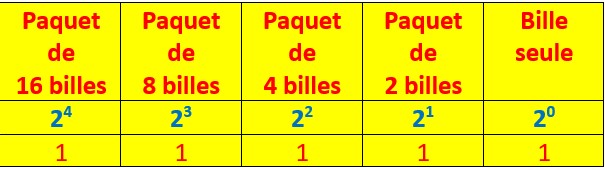
Je reprends le nombre précédent 11111 écrit en base 2.
Dans le tableau ci-contre chaque chiffre de ce nombre est réparti dans une case indiquant le nombre de paquet de 2,4,8,16 billes. En fait en base 2, on ne peut avoir que 0 ou 1 paquet.
Chaque paquet correspond à une puissance de 2.
Dans ce nombre 11111 j’ai une unité, une bille à droite.
Puis en allant vers la gauche, j’ai 1 paquet de 2 billes,
1 paquet de 4 billes,
1 paquet de 8 billes,
et enfin un paquet de 16 billes.
En additionnant toutes les billes, j’obtiens le nombre 31 écrit en base 10.
![]()
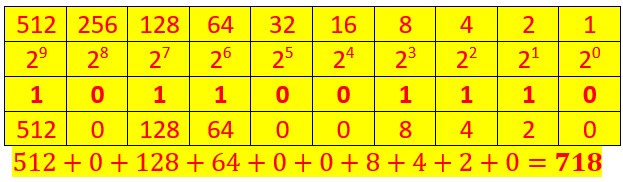
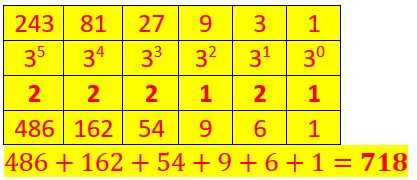
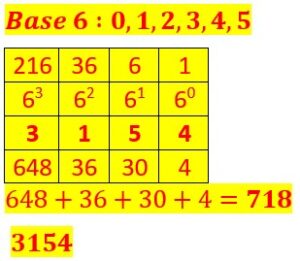
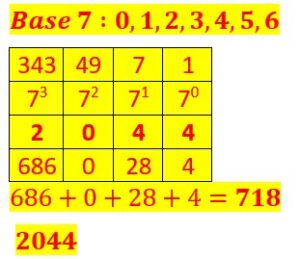
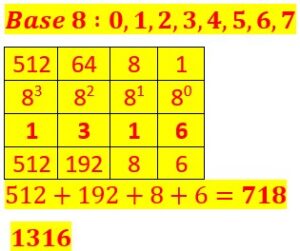
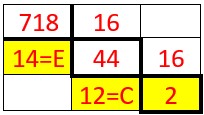
Soit le nombre 1011001110 écrit en base 2.
Nous procédons de la même façon que précédemment.
Et nous obtenons le nombre 718 écrit en base 10.
Conversion d’un nombre de la base 10 à la base 2
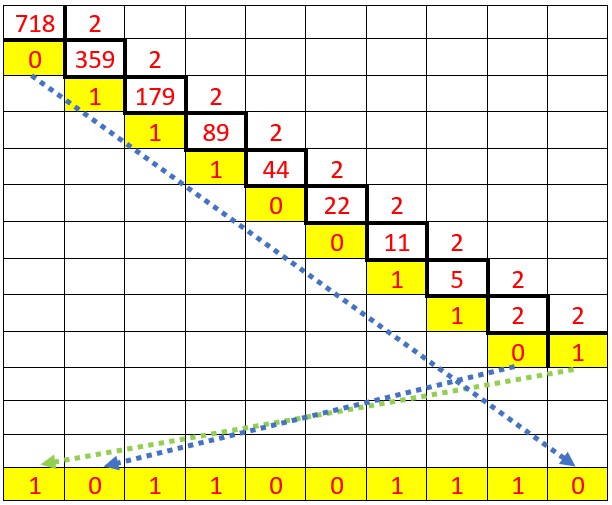
On procède par des divisions euclidiennes successives de diviseur 2 et on garde les restes de chacune des divisions .
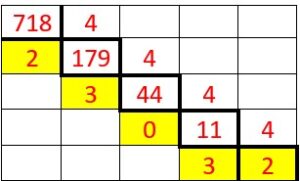
Par facilité, on va prendre le nombre 718 écrit en base 10.
Pour connaître le nombre de paquet de 2 je divise 718 par 2 :
j’obtiens 359 paquets de 2 et il reste 0 billes. J’ai donc 0 unité.
Pour connaître le nombre de paquets de 2 paquets de 2 ou paquets de 4, je divise 359 par 2 et j’obtiens 179 paquets de 4 et il reste 1 paquet de 2
Pour connaître le nombre de paquet de,2 paquets de,2paquets de 2 soit le nombre de paquets de 16, je divise 179 par 2 et j’obtiens 89 paquet de 16 et il reste un paquet de 8.
Pour connaître le nombre de paquets de 32 billes, je divise 89 par 4 et j’obtiens 22 paquets de 32 billes et il reste 0 paquet de 16.
Et ainsi de suite.
A la fin j’obtiens 1 paquet de 512 billes,
0 paquet de 256 billes,
1 paquet de 128 billes,
1 paquet de 64 billes,
0 paquet de 32 billes,
0 paquet de 16 billes,
1 paquet de 8 billes,
1 paquet de 4 billes,
1 paquets de 2 billes et
0 bille toute seule.
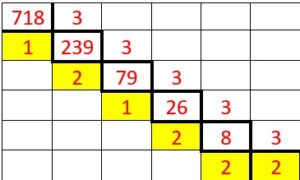
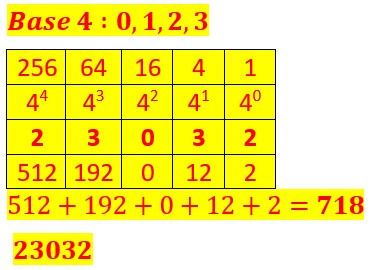
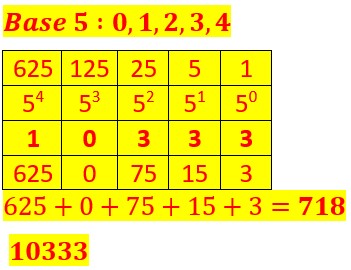
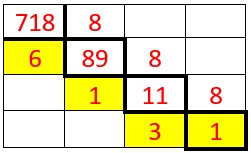
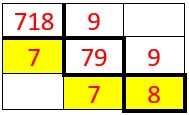
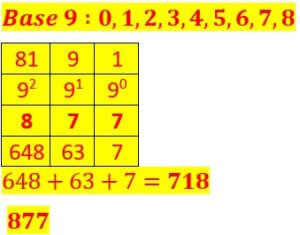
Bases 3,4,5,6,7,8,9.
On procède avec la même logique qu’en bas 2 Mais au lieu de répartir les objets, les billes en paquets de 2 on les regroupe en paquet de 3,4,5,6,7,8,9.
Voyons pour le nombre 718 écrit en base 10.
![]()
![]()

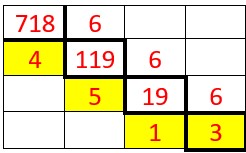
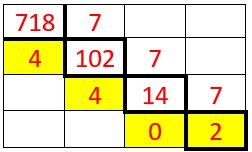
On peut continuer ainsi .
En base 10, on l’a vu.
En base 11. Il nous faudrait 11 signe Or on n’en a que 10. Il faudrait en inventer un.
Nous allons voir maintenant l’écriture d’un nombre en base 16
Base 16 ou hexadécimale

En base 16, nous avons besoin de 16 signes pour symboliser 16 chiffres. Or nous n’en avons que 10. Il nous suffit d’ajouter des lettres A,B,C;D,E,F pour obtenir nos 16 signes.
Mais il faut savoir que A en base 16 (hexadécimale) est égal à 10 en base 10 (décimale).
B en base 16 est égal à 11 en base 10.
C en base 16 est égal à 12 en base 10.
D en base 16 est égal à 13 en base 10.
E en base 16 est égal à 14 en base 10.
F en base 16 est égal à 15 en base 10.
A noter hexadécimal = hexa + décimal = 6+10=16.
Le chanteur Boby Lapointe (1922-1972) bien connu pour ses chansons avec jeux de mots et allitérations était aussi mathématicien. Il inventa un système pour écrire et nommer les nombres en bases 16 sans utiliser les symboles des nombres décimaux. Il breveta ce système en 1968 sous le nom de système bibi binaire. Mais il n’est pas du tout utilisé.
A quoi ça sert ?
Dans un ordinateur, il existe deux états : soit le courant passe, soit il ne passe pas. Lorsque le courant passe, cela correspond à un 1 numérique et lorsqu’il ne passe pas cela correspond à un 0.
Ainsi un succession de passage et de non passage du courant correspond à une succession de 1 et de 0 et donc à un nombre décimal.
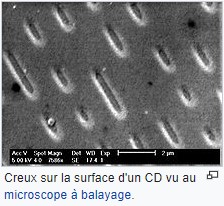
Un CD ou un DVD est constitué d’une succession de bosses et de creux. Chaque changement d’état (passage d’une bosse à un creux ou passage d’un creux à une bosse correspond à 1. Le non changement d’état correspond à 0.
On utilise donc le système binaire.
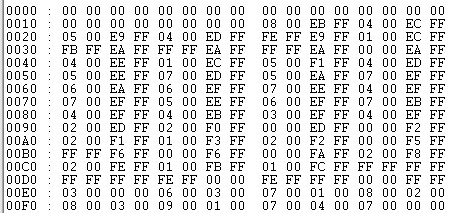
Sans aller dans les détails, on utilise le système hexadécimal, base 16, en informatique pour traduire d’une manière plus compacte la série de 1 et de 0 correspondant à un nombre décimal.
Ci-contre, la traduction en hexadécimal de la série de 1 et 0 d’un DVD personnel.
Base 60 ou sexagésimal
Sexagésimal signifie 60 : sexa=6 gésime=10 en latin.
le système sexagésimal permet de mesurer les angles, le temps, les coordonnées géographiques (latitude et longitudes)
La mesure d’angles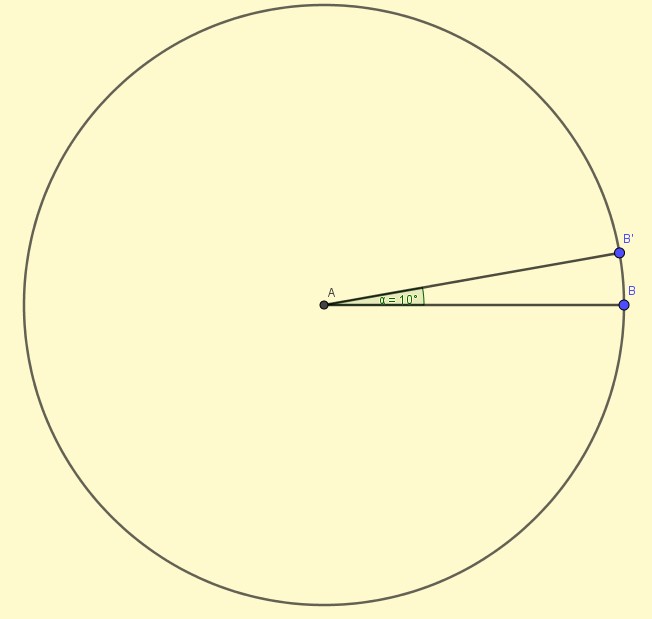

Soit un très petit angle dont la mesure est une seconde.
Si on prend un paquet de 60 de ces petits angles mis côte à côte, on obtient un angle de une minute.
Si on prend un paquet de 60 angles de une minutes mis côte à côte, soit 3600 petits angles de une seconde, on obtient un angle de un degré.
SI on prend un paquet de 6 fois soixante angles de un degré, on obtient un cercle.
Représenter un angle de une seconde, un écartement entre deux droites de une seconde est impossible sur le papier.
Il en est de même pour représenter un angle de une minute.
Même un angle de un degré est difficile.
Aussi a-t-on représenté un angle de 10 degré en vert sur la figure ci-contre. Il représente un angle de 10 fois un degré soit 10 fois soixante minutes, soit 10 fois 3600 secondes.
Attention : les minutes et les secondes sont ici des mesures d’angle qui n’ont rien à voir avec la mesure du temps, c’est pourquoi pour éviter toute équivoque on notera minute d’angle et seconde d’angle
Dans le logiciel GEOGEBRA l’affichage d’un point s’accompagne d’un bip sonore. Il est absent ici pour des raisons encore inconnues.
Ci contre une petite animation.
Il faut mettre le curseur à zéro avec la souris puis cliquer deux fois sur démarrer.
Un point s’affiche toutes les secondes environ suivant la vitesse de l’ordinateur. L’affichage d’un paquet de 60 points, soit 60 secondes, correspond à une minute.
On pourrait continuer en affichant un point toutes les minutes. Un paquet de 60 minutes correspondrait à une heure.
Mais cela prendrait beaucoup trop de temps.
On pourrait continuer encore en affichant un point toutes les heures.
Mais, arrivé là on change de base. Au lieu d’utiliser une numération à base 60 comme précédemment, on utilise une numération à base 24.
Ainsi un paquet de 24 heures correspond à un jour.
Pour les mois cela devient plus compliquer. Il faudrait faire des paquets de 28,29,30 ou 31 jours suivant la période où on se trouve. En effet les mois ont 30 ou 31 jours. Et le mois de février 28 ou 29 suivant les années.
Pour les années c’est pareille suivant qu’elles sont bissextiles ou non.

Une réponse
I was very pleased to uncover this site. I wanted to thank you for ones time for this particularly wonderful read!! I definitely liked every bit of it and I have you bookmarked to see new stuff on your blog.