Les identités remarquables
- par gabriel
- dans Calculs, Mathématiques, Non classé
- sur 27 janvier 2023

Définition

On appelle identité remarquable ou égalité remarquable une égalité s’appliquant à des nombres ou des expressions algébriques (polynômes). Elles permettent de calculer plus rapidement. Grâce à ces identités on peut simplifier des expressions algébriques, les développer ou les factoriser.
Ci-contre, trois expressions algébriques.
Pour la première :
On additionne deux nombres 3x et 5. Il s’agit bien d’une somme
(résultat d’une addition).
Puis on élève cette somme au carré.
Pour la deuxième :
On soustrait deux nombres 3x et 5. Il s’agit bien d’une d’une différence (résultat d’une soustraction)
Puis on élève cette différence au carré.
Pour la troisième :
On multiplie deux expressions. Il s’agit bien d’un produit (résultat d’une multiplication).
On multiplie une somme (3x+5) par une différence (3x-5)
Résolution en développant
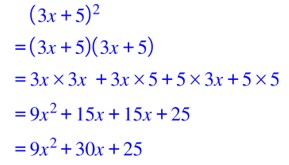
(3x+5) au carré c’est égal à (3x +5) multiplié par (3x+5)
Or on sait développer (3x+5)(3x+5)
Ensuite on réduit.
Au résultat on a :
9x² qui est le carré de 3x
30x qui est deux fois le produit de 3x et de 5
le carré de 5.
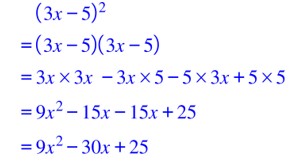
(3x-5) au carré c’est égal à (3x -5) multiplié par (3x-5)
Or on sait développer (3x-5)(3x-5)
Ensuite on réduit.
Au résultat on a :
9x² qui est le carré de 3x
30x qui est deux fois le produit de 3x et de 5
le carré de 5.
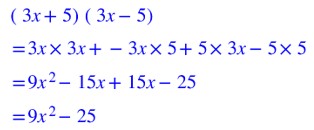
On sait développer (3x+5)(3x-5)
Ensuite on réduit.
Au résultat on a :
9x² qui est le carré de 3x
le carré de 5.
Les formules
Première identité remarquable.
Soit a et b deux nombres ou expressions algébriques quelconques.

Deuxième identité remarquable.

Troisième identité remarquable.

Conseils de calcul.
Positionner le curseur t sur 0 puis le faire glisser vers la droite en s’arrêtant à chaque étape pour lire le texte.
Développement et factorisation
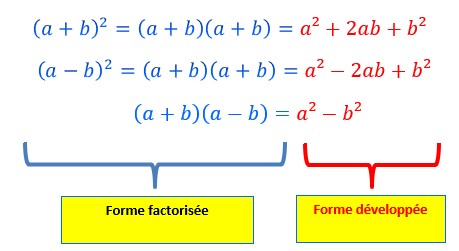
(a+b)² est un produit de facteur puisque c’est la multiplication de deux facteurs (a+b)(a+b).
En appliquant la formule on est passé d’une forme factorisée à une forme développée.
Une forme développée est une suite d’addition ou soustraction de plusieurs termes. C’est cas de a²+2ab+b² qui est une suite d’addition de trois termes a², 2ab et b².
Il faut savoir aussi passer de la forme factorisée à la forme développée.
Nous allons voir comment sachant qu’il faut lire les égalités dans l’autre sens.
Première identité remarquable.
Dans l’exemple ci-contre on a trois termes et uniquement des signes + donc il pourrait s’agir de la première identité remarquable.
Peu importe si les termes ne sont pas dans l’ordre habituel de l’identité remarquable. Il suffit soit de les remettre en ordre soit de repérer deux carrés.
Un fois les carrés repérés, le terme restant fait office éventuellement de double produit des deux nombres.
Deuxième et troisième identité remarquable.
Ajoutez votre titre ici
Démonstration géométrique des trois identités.
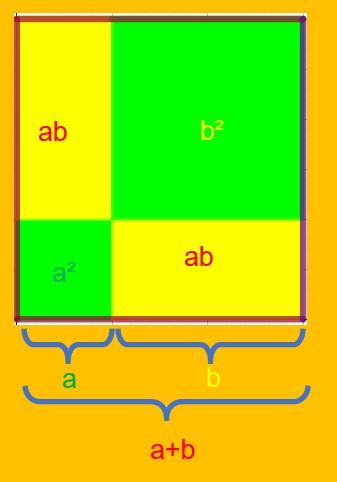
Le côté du petit carré vert est égal à a.
Le côté du grand carré vert est égal à b
La longueur d’un rectangle jaune est égale à b
La largeur d’un rectangle jaune est égale à a
Le côté du grand carré entouré de marron est égal à a+b.
L’aire du grand carré entouré de marron est égale à (a+b)².
L’aire du petit carré vert est égale à a²
L’aire d’un rectangle jaune est égale à axb=ab
L’aire des deux rectangles jaunes est égale à 2ab
L’aire du grand carré vert est égale à b².
L’aire totale du carré entouré de marron est égale à
L’aire du petit carré vert plus
l’aire des deux rectangles jaunes plus
l’aire du grand carré vert
(a+b)²= a²+2ab+b²
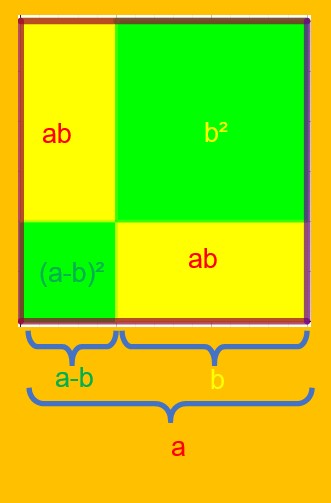
Le côté du grand carré entouré de marron est égale à a.
Le côté du grand carré vert est égale à b.
Le côté du petit carré vert est donc égale à a-b.
La longueur d’un rectangle jaune est égale à b.
La largeur d’un rectangle jaune est égale à a-b.
L’aire du grand carré entouré de marron est égale à a².
L’aire du petit carré vert est égale à (a-b)².
L’aire d’un rectangle jaune est égale à (a-b)b.
L’aire des deux triangles jaunes est égale à 2(a-b)b.
L’aire du grand carré vert est égale à b².
L’aire du grand carré est égale à
l’aire du petit carré vert plus
l’aire des deux rectangles jaunes plus
l’aire du grand carré vert.
a²=(a-b)²+2(a-b)b+b²
a²=(a-b)²+2ab-2b²+b²
a²=(a-b)²+2ab-b²
a²-2ab+b²=(a-b)²
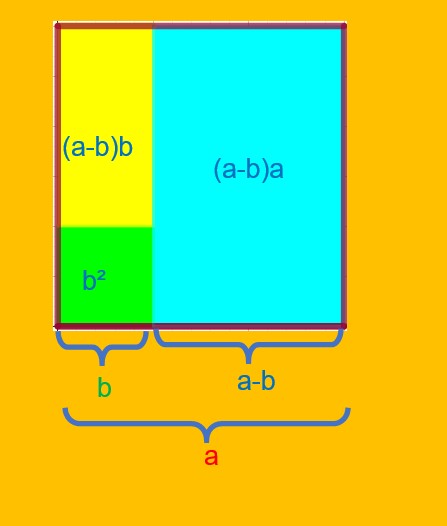
Le côté du grand carré entouré de marron est égal à a.
Le côté du petit carré vert est égal à b.
La Longueur du petit rectangle jaune est égale à a-b.
La largeur du petit rectangle jaune est égale à a.
La longueur du grang rectangle bleu est égale à b.
La largeur du grand rectangle bleu est égale à a-b.
L’aire du grand rectangle entouré de marron est égale à a².
L’aire du petit rectangle vert est égale à b².
L’aire du petit rectangle jaune est égale à b(a-b)
L’aire du grand rectangle bleu est égale à b(a-b).
L’aire du grand carré entouré de marron est égale à
l’aire du petit carré vert plus
l’aire du rectangle jaune plus
l’aire du rectangle bleu.
a²=b²+b(a-b)+a(a-b)
a²-b²=b(a-b)+a(a-b)
En factorisant par (a-b)
a²-b²=(a+b)(a-b)