Inéquations
- par gabriel
- dans Equations inéquations, Mathématiques
- sur 19 février 2023

Les symboles des inégalités
![]()
Le nombre ou l’expression qui est à gauche de ce symbole est plus grand que le nombre ou l’expression qui est à droite.
Ce symbole est en quelque sort un angle dont la partie ouverte est à gauche et le sommet à droite. La partie ouverte est plus grande que le sommet. Donc ce qui est du côté de la partie ouverte est plus grand que ce qui est du côté du sommet.
Exemple ![]()
Trois est plus grand que deux
![]()
![]()
Le nombre ou l’expression qui est à gauche de ce symbole est plus petite que le nombre ou l’expression qui est à droite.
Le sommet de l’angle est à gauche et sa partie ouverte est à droite. Ce qui est à gauche est plus petit que ce qui est à droite.
Exemple :![]()
Deux est plus petit que trois.
Le nombre ou l’expression qui est à gauche du symbole est plus grand ou égal au nombre ou l’expression qui est à droite.
Il est soit plus grand soit égal. Il ne peut pas être les deux à la fois.
Exemple :![]()
Trois est bien plus grand ou égal à deux puisqu’il est plus grand que deux.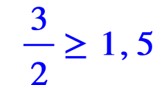
Trois demis est bien plus grand ou égal à un virgule cinq puisqu’il est égal à un virgule cinq.
![]()
Le nombre ou l’expression qui est à gauche du symbole est plus petit ou égal au nombre ou l’expression qui est à droite.
Il est soit plus petit soit égal. Il ne peut pas être les deux à la fois.
Exemple :![]()
Deux est bien plus petit ou égal à trois puisqu’il est plus petit que trois.
Un virgule cinq est bien plus petit ou égal à trois demis puisqu’il est égal à trois demis.
Inégalités dans les réels positifs et négatifs
![]()
Il est évident que 3 est plus grand que 2
![]()
Que se passe-t-il si on multiplie les deux membres de cette inégalité par -1 ?
![]()
Il est évident que cette fois -3 est plus petit que -2
On est donc obligé de changer le sens de l’inégalité.
![]()

![]()
Il en est de même si on divise les deux membres de l’inégalité par -1.
On ne change pas le sens d’une inégalité quand on multiplie (ou on divise) les deux membres par un même nombre positif.
On change le sens d’une inégalité quand on multiplie (ou on divise) les deux membres par un même nombre négatif.
Les intervalles
Inéquation.
![]()
Il s’agit de trouver les valeurs du nombre algébrique x tel que 4 fois cette valeur plus 2 soit supérieure à 2 fois cette valeur plus 5.
![]()
On utilise dans un premier temps les mêmes règles que celles pour résoudre une équation.
On isole les inconnues dans un membre et les nombres connus dans l’autre à condition de changer les signes des nombres qui changent de membre.
Isolons les inconnues dans le premier membre et les nombre connus dans le second.
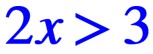
On réduit chaque membre : on calcule dans chacun des membres.

Pour trouver les valeurs de x il nous faut diviser les deux membres par 2.
Ainsi pour que l’inéquation de départ soit vérifier, il faut que x soir supérieur à 3 demis, c’est-à-dire supérieur à 1,5
On peut aussi lire l’inégalité à l’envers (en commençant par la droite) et cela devient 1,5 doit être plus petit que x.
Vérifions: Prenons x= 5 qui est supérieur à 1,5
4×5+2>2×5+5
22>15
Ce qui est exacte.
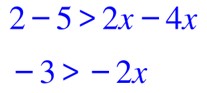
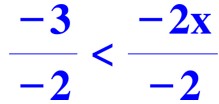
Voyons ce que cela ferait si nous isolions les inconnues dans le second membre et les nombre connus dans le premier.
Pour trouver la valeur de x, il faut diviser les deux membres de l’inéquation par -2 qui est un nombre négatif.
Donc, il faut changer le sens de l’inéquation comme pour une inégalité.


On aboutit à la solution que trois demis doit être plus petit que x .
Ou ce qui revient au même (en lisant l’inéquation à l’envers ) que x doit être plus grand que trois demis ou un virgule cinq.

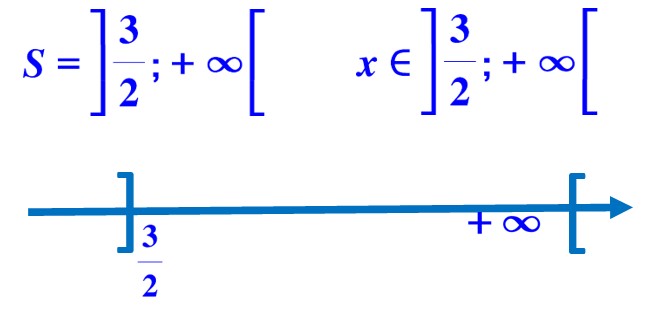
Différentes façons de présenter la solution à l’inéquation.
Pour que ![]() soit vérifiée, il faut que x soit strictement plus grand que 3/2.
soit vérifiée, il faut que x soit strictement plus grand que 3/2.
Cela veut dire que x doit être plus grand que 3/2 sans être égal à 3/2.
Signe d'un produit de facteurs.
Soit deux nombres ou deux expressions algébriques A et B.
Etudions le signe de leur produit AB, A x B.
Cliquer sur initialisation.
En vert nous avons un produit de facteurs dont on doit trouver le signe en fonction de la variable t qui prend des valeurs entre -20 net +20.
Cliquer sur premier facteur.
Apparaît l’expression du premier facteur avec en dessous sa valeur en fonction de la valeur de t.
Pour t=-20 ce premier facteur A vaut -44.
Faire glisser le curseur t vers la droite. Le facteur A prend différentes valeurs.
Tout d’abord, il est négatif . Puis pour t=2, il est nul et devient ensuite positif.
Cliquer sur deuxième facteur.
De même faire glisser le curseur t vers la droite.
Le deuxième facteur est tout d’abord positif. Il est égal à 0 pour t=12, puis devient négatif.
Cliquer sur produit.
Apparaît le produit des deux facteurs.
Il est d’abord négatif.
Il est égal à 0 pour t=2
Il devient ensuite négatif.
Il est à nouveau égal à 0 pour t=12
Il redevient négatif ensuite.
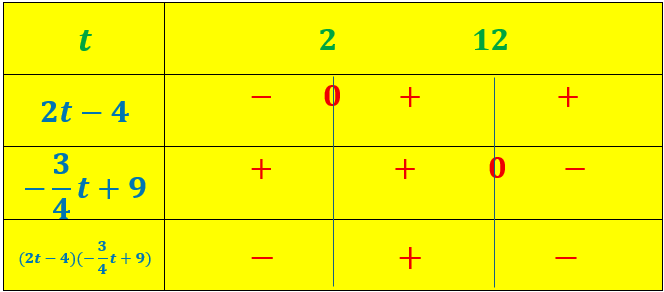
Nous pouvons résumer tous ces résultats dans un tableau appelé tableau de signes dont nous allons voir la constructions dans divers exemples ci-dessous.
Résolution pratique : tableaux de signes
Premier exemple : tableau de signes d'un produit de deux facteurs

Quel est le signe de ![]()
en fonction (suivant) les valeurs de x variant de -∞ à +∞
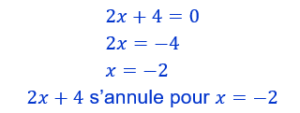
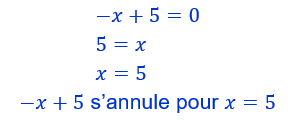
première étape :
On cherche les zéros de chacun des facteurs autrement dit on cherche pour quelle valeur de x chacun des facteurs s’annule (est égal à zéro. les calculs ci-contre peuvent être exécutés mentalement.
Deuxième étape
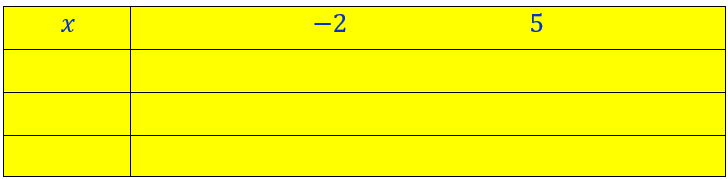
On construit un tableau de 4 lignes et 2 colonnes.
Dans la première ligne et la deuxième colonne on note par ordre croissant les valeurs de x qui annulent l’expression A.
Troisième étape
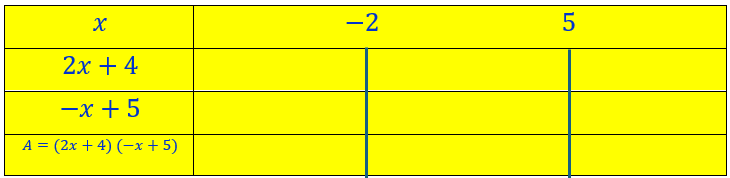
On note dans la première colonne les facteurs composant l’expression A.
Dans la dernière ligne de cette première colonne on note l’expression A.
Puis dans la seconde colonne à partir de la deuxième ligne on trace des traits de séparation sous les valeurs de x annulant l’expression A;
Quatrième étape
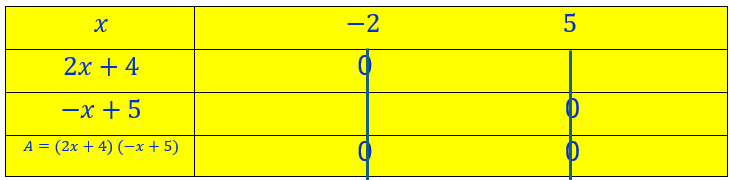
2x+4 s’annule pour x=-2. On note 0 sous le -2 dans la deuxième ligne
-x-1 s’annule pour x=5. On note 0 sous le 5 dans la troisième ligne.
A s’annule pour x= – 2 et x=5. On note 0 sous le -2 et le 5 dans la quatrième ligne .

Cinquième étape
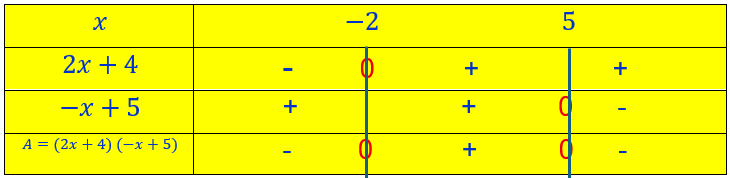
Placement des signes dans le tableau.
Il faut déterminer pour chacun des facteurs son signe :

![]()

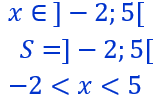
Résolution de l’inéquation![]()
On construit le tableau de signe du produit de facteurs inscrit dans le premier membre de l’inéquation.
Dans la dernière ligne du tableau, on regarde dans quelle case le produit de facteurs est positif.
Il est positif pour les valeurs de x comprises entre -2 et 5
On traduit cela par une expression algébrique en précisant les résultats suivant :
L’inéquation nous demande de trouver les valeurs de x pour lesquelles l’expression du premier membre doit être strictement positive. Cela signifie que notre expression ne doit pas être nulle. Donc, il faut éliminer les valeurs qui annulent cette expression soit -2 et 5.On traduit cela par des crochets ouverts.
On peut présenter la solution sous trois formes différentes.
![]()

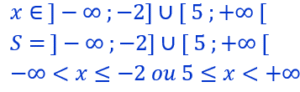
Résolution de l’inéquation ![]()
On procède de la même manière avec le tableau de signes.
Cette fois on demande de trouver les valeurs de x pour lesquelles l’expression algébrique est plus petite que 0 ou égale à 0.
Dans le tableau de signe, il existe deux cases correspondant à cette condition. Comme les valeurs -2 et 5 qui annulent l’expression sont des solutions on les indique avec des crochets fermés. Les valeurs moins l’infini et plus l’infini sont indiquées par des crochets ouverts puisqu’on ne eut jamais atteindre l’infini.
deux séries de valeurs sont possibles, on, les réunit par le symbole de la réunion U qui correspond à la conjonction ou :
x est soit plus petit que -2 soit plus grand que 5. Il ne peut pas être à la fois plus petit que -2 et plus grand que 5.