Fonction dérivée d’une fonction.

par gabriel
dans Fonctions, Mathématiques
sur 16 mars 2023

Ce qu'il faut savoir

La notion de taux de variation
https://gabriel-brissot.fr/2022/09/taux-de-variation-dune-fonction

La notion de nombre dérivé.
https://gabriel-brissot.fr/2019/10/nombre-derive

Animation

Cliquer une première fois sur le bouton bleu “Initialiser/Animer” : t=-2.5.
Cliquer une seconde fois : le point M0 se déplace sur la courbe pour les valeurs de t variant de 0.25 en 0.25.
On peut suspendre le déplacement en cliquant sur le petit bouton pause. Cela permet de bien regarder la situation.
On peut déplacer le curseur avec la souris dans les deux sens.

Soit la fonction :

La variable t prend les valeurs dans l’intervalle

La valeur de t change avec le curseur rouge.
Un point M₀ se déplace sur la courbe représentative de la fonction.
En chacun des points M₀, on peut calculer le nombre dérivé correspondant qui est aussi le coefficient directeur ou pente de la tangente en ce point.
Nous avons vu comment calculer ce nombre dérivé dans le chapitre sur le taux de variation.
Dans l’animation il est noté pour chaque valeur de t, la position de M₀, la valeur du nombre dérivé et même l’équation de la tangente qui est tracée.

Pour chacun des points M₀ de la courbe il existe un nombre, appelé nombre dérivé qui est le coefficient directeur ou pente de la tangente en ce point. Puisque les points M sont déterminés en fonction de la variable x, il en sera de même pour les nombre dérivées. On a créé ainsi une nouvelle fonction appelée fonction dérivée Cette nouvelle fonction dérivée est particulière à la fonction étudiée au début.

Dérivée de quelques fonctions

Dérivée de la fonction constante

Une fonction constante est représentée par une droite parallèle à l’axe des abscisses (axe des x ) passant par le point d’ordonnée k.
Son taux d’accroissement sur un intervalle quelconque est évidemment nul. Le nombre dérivé en tout point de la droite est nul et sa fonction dérivée est égale à 0.

Dérivée d'une fonction linéaire

Cas général d’une fonction linéaire :

Dans l’exemple ci contre a=3.
Comme d’habitude appliquons la formule donnant le nombre dérivé au point d’abscisse x₀.

Dérivée d'une fonction affine

Dans la fonction particulière que nous avons choisi a=2 et b=1.
Pour chacun des points M de la fonction (coordonnées écrites en vert) nous obtenons un nombre dérivé qui est l’ordonnée du point M’ ( coordonnées écrites en rouge).
Ce nombre dérivé est la pente de la tangente à la courbe (en vert) au point M
Le point M’ décrit une courbe qui est la fonction dérivée (en rouge
Pour des raisons techniques dans géogébra, la variable est désignée par t et non par x.
Il est évident que la tangente au point M à la droite est la droite elle même.

La formule générale de la fonction affine est :

Elle est définie pour tout x appartenant à l’ensemble des réels.
Il existe donc un nombre dérivé pour tout point M dont l’abscisse appartient à l’ensemble des réels.
Calcul de la fonction dérivée.
On utilise la formule donnant le nombre dérivé au point M₀ d’abscisse x₀.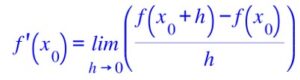

comme

On en déduit

En calculant dans les crochets :

Comme h tend vers 0 mais n’est pas égal à 0, on peut simplifier par h :
Quel que soit le nombre le point M₀ et donc son abscisse x₀, le nombre dérivé sera égal à a. La fonction dérivée sera donc égale à a.

Dérivée de la fonction carrée

Pour chacun des points M de la fonction (coordonnées écrites en vert) nous obtenons un nombre dérivé qui est l’ordonnée du point M’ ( coordonnées écrites en rouge).
Ce nombre dérivé est la pente de la tangente à la courbe (en vert) au point M.
L’équation de cette tangente est écrite en violet.
Le point M’ décrit une courbe qui est la fonction dérivée (en rouge)

Le graphique de la fonction est en vert. Sa variable est t.

Le graphique de la fonction dérivée est en rouge. Sa variable est t.
La tangente au point M est en violet. Sa variable est x.

L’équation de la fonction est :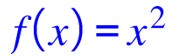

Elle est définie pour tout x appartenant à l’ensemble des réels.
Il existe donc un nombre dérivé pour tout point M dont l’abscisse appartient à l’ensemble des réels.
On calcule le nombre dérivé en un point de la courbe en utilisant la formule :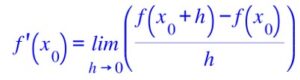

On développe l’identité remarquable :

On réduit :

On factorise par h :

Comme h tend vers 0 mais n’est pas égal à 0 on peut simplifier par h :

Cette égalité est valable pour tout x₀et donc pour tout x.
L’équation de la dérivée est :

Dérivée de la fonction puissance

exemples:

La formule générale de la fonction puissance est pour tout x et n appartenant à l’ensemble des réels :

Calculons le nombre dérivé pour x₀.

la valeur de (x₀+h)ⁿ nous est donné par la formule du binôme de Newton à savoir :

= x₀ puissance n plus la combinaison de 1 élément pris parmi n éléments multiplié par x₀ puissance n multiplié par h +…… En remplaçant dans la formule :

On peut éliminer les x₀ puissance n :

On factorise le numérateur par h et on simplifie par h car h tend vers 0 mais n’est pas égal à 0:

Puisque h tend vers 0 tous les termes contenant h peuvent être éliminés, et il reste :

Or la combinaison de 1 élément pris parmi n est :

Donc :

La formule a bien été démontrée. On aurait pu aussi faire une démonstration par récurrence.

Dérivée de la fonction du second degré.

Le graphique de la fonction est en vert. Sa variable est t.
Le graphique de la fonction dérivée est en rouge. Sa variable est t.
La tangente au point M est en violet. Sa variable est x.

L’équation générale d’une fonction du second degré est :

Elle est définie pour tout x appartenant à l’ensemble des réels.
Il existe donc un nombre dérivé pour tout point M dont l’abscisse appartient à l’ensemble des réels.
Nous utilisons la formule permettant de calculer le nombre dérivé en un point M₀ d’abscisse x₀.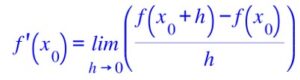

On développe l’identité remarquable et on développe le reste de l’expression.

On développe encore :

On réduit :

On met h en facteur :

Comme h tend vers 0 sans jamais l’atteindre, on peut simplifier par h :

h tendant vers 0 ah s’annule :

On obtient le nombre dérivé pour chacun des point M0 d’abscisse x0.
Cette formule sera valable pour tout x. La dérivée de notre fonction est donc :

Dérivée de la fonction inverse.

Le graphique de la fonction est en vert. Sa variable est t.
Le graphique de la fonction dérivée est en rouge. Sa variable est t.
La tangente au point M est en violet. Sa variable est x.

Voyons grâce à la formule de la fonction puissance qui est acquise un moyen de calcul de cette dérivée.

La division par 0 n’a aucun sens. Cette fonction n’est pas définie pour x=0. Elle est définie pour tout x appartenant à l’ensemble des réels sauf pour x=0.
Utilisons la formule du nombre dérivé en un point x₀ d’une fonction.

Ce qui donne :

Réduisons au même dénominateur les deux fractions du numérateur :

Après addition de ces deux fractions :

En réduisant :

Pour diviser deux fractions on multiplie la première par l’inverse de la seconde :

Comme h tend vers 0, hx₀ aussi :

On obtient le nombre dérivée pour tout point M0 de la courbe d’abscisse x0. On obtiendra le même résultat pour tout point M d’abscisse x.
La fonction dérivée de la fonction inverse est donc :

Dérivée de la fonction racine carrée.

Petit rappel bien pratique :

On ne peut prendre la racine carrée que d’un nombre positif ou nul. Donc x doit être positif.
Utilisons la formule du nombre dérivé en un point M d’abscisse x₀.

Ce qui donne pour la fonction racine carrée :

Le numérateur de la fraction a pour expression conjuguée :

Multiplions le numérateur et le dénominateur de la fraction par cette expression conjuguée qui ne peut pas être nulle.

Développons le numérateur qui est une identité remarquable (la troisième) :

Réduisons le numérateur :

Simplifions par h qui tendant vers 0 n’est pas égal à 0 :

Comme h tend vers 0 on peut écrire :

Donc :

Pour chaque valeur de x0 on obtient un nombre dérivé.
La fonction dérivée sera donc :

Dérivée de la fonction exponentielle

Dérivée de la fonction logarithme népérien

Dérivée du produit de deux fonctions

Exemples de résolution :

Démonstration:

Dérivée du quotient de deux fonctions

Ajoutez votre titre ici

Dérivées des fonctions composées.

Un exemple :

Soit une fonction f(x) qui à tout nombre x fera correspondre un nombre nouveau noté f(x) que l’on peut noter aussi X.
Soit une fonction g(x) qui au nouveau nombre f(x) ou X fait correspondre un autre nouveau nombre g(f(x)) ou g(X)

Prenons un exemple :
A tout nombre x la fonction f fait correspondre le nombre x+1 = X
x a pour image x+1.
A tout nombre x+1=X la fonction g fait correspondre le carré de ce nombre soit X² = (x+1)².
(x+1) a pour image (x+1)² ou X a pour image X².

Il s’agit de calculer la dérivée de cette fonction finale g(f(x)) qui est une fonction composée, c’est-à-dire une fonction de fonction. g est la fonction de la fonction f . On peut écrire les fonctions composées avec un opérateur appelé rond et noté º : gºf. Et gºf =g(f(x)).
La dérivée d’une fonction composée (gºf)(x)est égale au produit de la dérivée de la fonction f(x) par rapport à x par la dérivée de la fonction g par rapport à f(x).

Tableaux des dérivées

Dérivées des fonctions simples.

D’autres dérivées de fonctions simples

Dérivées de la somme, du produit, du quotient de deux fonctions.

Soit u(x) et v(x) deux fonctions qu’on désignera pour simplifier par u et v.

Dérivées des fonctions composées.

Dérivées successives et classe d'une fonction

Dérivée seconde

Dérivée nième

Opérations sur les fonctions

Formule de Leibniz

Classe d'une fonction

Exemples de calculs de dérivées

Utilisation de la formule de la dérivée d'une fonction puissance

On peut utiliser avantageusement cette formule chaque fois que l’on peut traduire une fonction à l’aide d’une fonction puissance.
C’est la cas ci-contre x écrit seul est comme x élevé à la puissance 1.
Le calcul de la dérivée donne x puissance 0.

Or tout nombre élevé à la puissance 0 est égal à 1

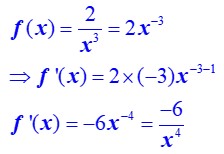
Dans ce cas nous utilisons les puissances négatives. Lorsqu’un nombre ou une variable est situé au dénominateur d’une fraction et s’il est élevé à une puissance positive, on peut l’écrire au numérateur avec une puissance négative.
Lorsqu’on a calculé la dérivée avec cette méthode, on rétablit la position au dénominateur pour avoir une puissance positive.

Pour les racines carrées on utilise les exposants fractionnaires. Prendre la racine cubique d’un nombre élevé à la puissance 5 revient à élever ce nombre à la puissance 5/3.
Il suffit de bien connaître les opérations avec les fractions.
ensuite on rétablit l’écriture avec des exposants entiers.

Un petit cocktail histoire de s’amuser un peu. Comment ferait-on sans les exposants fractionnaires et négatifs ?

Fonction dérivée d’une fonction.