Epreuve de Bernoulli, schéma de Bernoulli, loi binomiale.
- par gabriel
- dans Articles nouveaux, Mathématiques, Probabilités
- sur 11 mai 2024
Table des matières
Exemple
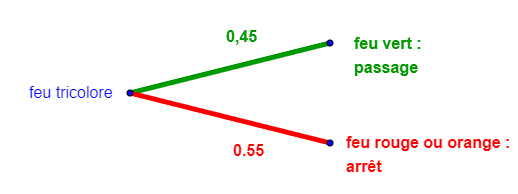
Ci-contre un feu tricolore. qui fonctionne normalement. Il faut cliquer sur « initialisation / animation » et recliquer dessus pour « allumer le feu » (!).
L’alternance des couleurs est la suivante :
rouge pendant 60 secondes,
vert pendant 54 secondes,
orange pendant 6 secondes, avant de repasser au rouge.
Le temps total d’un cycle est de 120 secondes.
Ainsi la probabilité lorsqu’on arrive devant le feu tricolore d’avoir un feu rouge est :![]()
La probabilité d’avoir un feu vert est :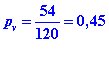
La probabilité d’avoir un feu orange est :![]()
En additionnant toutes ces probabilités qui correspondent aux 3 possibilités, aux 3 issues nous obtenons bien le chiffre 1.![]()
Epreuves de Bernoulli
Feu tricolore
Lorsque le feu est rouge je dois m’arrêter.
Lorsque le feu est orange, je dois aussi impérativement m’arrêter.
Mais lorsque le feu est vert, je dois continuer ma route.
Considérons comme un succès le fait de pouvoir continuer ma route et un échec (le contraire d’un succès) le fait de devoir m’arrêter.
Si le feu est vert, je peux continuer c’est un succès.
Si le feu n’est pas vert (s’il est rouge ou orange), je dois m’arrêter c’est un échec ou un non succès.![]()
Nous avons ainsi une alternative, deux possibilités seulement, deux issues.
La probabilité du succès, de pouvoir passer au feu vert est :![]()
la probabilité de l’échec, du non succès sera donc :![]()
puisque c’est une issue contraire au succès. Cette probabilité correspond bien à la somme des probabilités pour le feu orange et le feu rouge.
Définition
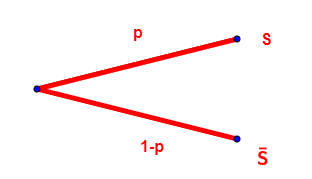

Une épreuve de Bernoulli de paramètre p (0≤p≤1) est une expérience aléatoire (soumise au hasard) comportant une alternative, donc deux issues, le succès ou l’échec. On note alors p la probabilité d’obtenir le succès et 1-p la probabilité d’obtenir l’échec.
Soit X une variable aléatoire et p un nombre réel tel que 0 ≤ p≤ 1. X suit une loi de Bernoulli de paramètre p si :
l’univers de X est Ω(X) = {0 ; 1} ;
P(X = 1) = p et P(X = 0) = 1 – p.
On note la loi de Bernoulli par B(p).
Propriétés

Démonstration :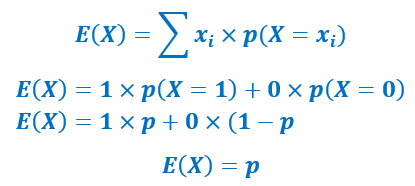
Si on répète certain nombre de fois une épreuve, nous obtenons chaque fois une probabilité p pour que l’expérience soit une réussite. La moyenne de ces probabilités correspond à l’espérance mathématique E. Elle est définie par la somme du produit de chaque valeur de la variable aléatoire xi par sa probabilité p(X=xi) correspondante. On la calcule à partir du tableau de la loi de la variable aléatoire.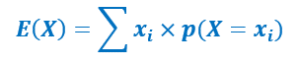
Pour l’épreuve de Bernoulli on n’a qu’une seule épreuve.

Démonstration :
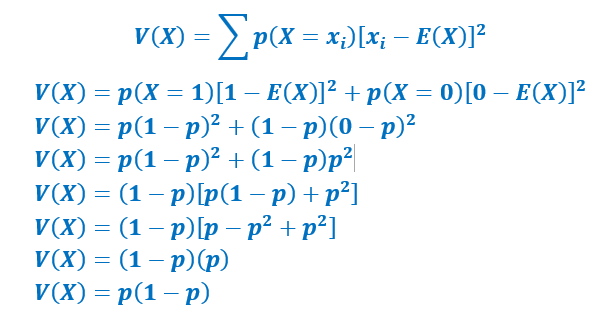
La Variance est un nombre qui donne la moyenne de la dispersion des résultats autour de l’espérance.
On la calcule en effectuant la somme des produits de chaque probabilité de la variable aléatoire X par le carré de l’écart à la moyenne de la valeur correspondante de cette variable aléatoire [xi-E(X)]2. ![]()
Exemples



En lançant une pièce de monnaie, elle retombe soit sur le côté pile soit sur le côté face.
On a donc une alternative, soit deux possibilités, deux issues.
Comme la pièce est bien équilibrée, elle a autant de chance de tomber sur le côté pile que sur le côté face.
Admettons que le succès soit le côté pile. La probabilité correspondante est p=0,5.
La probabilité contraire, la pièce tombe sur le côté face est également de 0,5 car 1-p=1-0,5=0,5. L’épreuve de Bernoulli se notera B(0,5)
Par contre si la pièce est pipée, c’est à dire truquée. Si on a collé sur son côté face une certaine quantité de pâte à modelée. Ce côté face étant plus lourd aura plus tendance de tomber contre le sol et ainsi on aura plus de chance d’avoir le côté pile en vue.
Admettons que cette probabilité d’avoir le côté pile soit p= 0,7.
La probabilité d’avoir le côté face sera 1-p=1-0,7=0,3. Cette épreuve de Bernoulli se notera B(0,7).

Dans un jeu de 52 cartes on tire une carte au hasard. C’est un succès si on tire une figure, si non c’est un échec.
Une figure est une carte représentant un personnage; Il s’agit des cartes suivantes : Valet, Dame, Roi.
Il existe donc trois figures dans chacune des couleurs : trèfle carreau, coeur, pique.
Il existe donc 3 X 4 = 12 figures dans un jeu de 52 cartes.
La probabilité de tirer une figure sera donc ![]()
Et la probabilité de ne pas tirer une figure sera :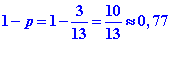
L’épreuve de Bernoulli en question se notera 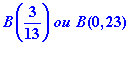
Noter qu’on aurait pu prendre comme succès le fait de ne pas tirer une figure !

Dans un atelier on peint en bleu des joints toriques. On estime que 5% de ces joints ne sont pas peint correctement.
On tire au hasard un joint torique, s’il est défectueux , s’il est mal peint on considère que c’est un succès. Dans le cas contraire si le joint est peint correctement on considère que c’est un échec.
La probabilité de tirer un joint défectueux est :
La probabilité d’avoir un joint correctement peint est :![]()
L’épreuve de Bernoulli se notera ![]() .
.
Shéma de Bernoulli

Reprenons l’épreuve de Bernoulli concernant les feus tricolores.
Cette fois, il existe trois feus successifs.
Pour décrire la situation, nous avons besoin d’un arbre de probabilités construit ci-contre.
Au premier feu, première alternative donc deux possibilités.
Soit le feu est vert, soit il n’est pas vert notés respectivement :![]()
Au deuxième feu, deuxième alternative, encore deux possibilités parmi les deux possibilités précédentes.
En effet, si le premier feu est vert, nous avons deux possibilités ![]() pour le deuxième feu.
pour le deuxième feu.
Et si le premier feu n’est pas vert, nos avons aussi les deux mêmes possibilités ![]() pour le deuxième feu.
pour le deuxième feu.
Au troisième feu, troisième alternative et nous avons deux possibilités ![]() parmi les quatre possibilités précédentes.
parmi les quatre possibilités précédentes.
En suivant toutes les branches de l’arbre une par une, nous obtenons toutes les possibilités au sujet de nos trois feus tricolores.
Exemples :
le premier feu est vert, le deuxième est vert, le troisième est vert.
le premier feu est vert le deuxième n’est pas vert, le troisième n’est pas vert .le premier feu n’est pas vert, le deuxième et le troisième ne sont pas verts.
Ainsi nous avons 8 cas possibles que nous allons résumé dans le prochain arbre avec les probabilités correspondantes.
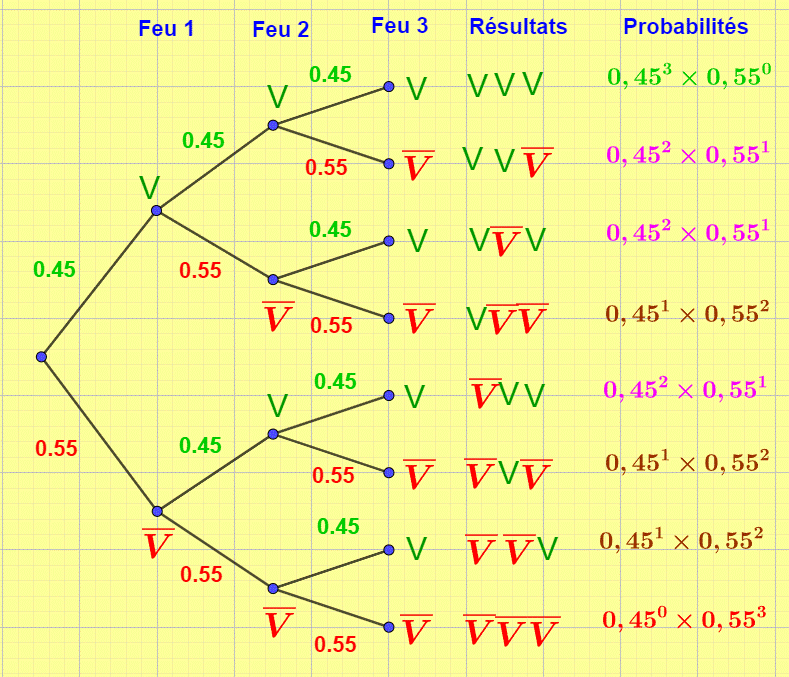
Quelle est la probabilité que les trois feus soient verts ?
Cette éventualité correspond à la première branche ![]() . or nous savons que la probabilité pour qu’un feu soit vert est de 0,45.
. or nous savons que la probabilité pour qu’un feu soit vert est de 0,45.
Nous pouvons donc écrire :![]()
Dans le tableau, nous avons rajouté (0,55)0 qui est égal à 1 et qui ne change rien au résultat. Nous verrons plus loin pourquoi cet artifice.
Quelle est la probabilité pour que le premier feu soit rouge, puis le deuxième soit vert et le troisième soit rouge dans cet ordre ci.
Il s’agit de la branche ![]() .
.![]()
Quelle est la probabilité pour qu’un seul feu soit vert.
Dans ce cas on trouve trois possibilités : ![]()
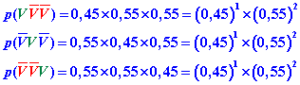
On trouve trois fois le même résultat. C’est le nombre de 1 feu vert parmi 3.


Résumons :
Au départ on considère une épreuve de Bernoulli qui est une alternative, deux possibilités seulement, l’une considérée comme un succès ![]()
et l’autre comme un non succès, non S ![]()
On détermine le paramètre de cette épreuve comme étant la probabilité du succès. ![]()
L’échec ou non succès aura comme probabilité ![]()
Cette épreuve de Bernoulli sera nommée ![]()
On répète n fois .cette épreuve de Bernoulli (3 fois dans notre exemple puisqu’il a trois feus tricolores), Cette répétition est appelée schéma de Bernoulli.
Avec le schéma de Bernoulli on obtient, glace à l’arbre, tous les détails.
Il existe une seule modalité pour n’avoir aucun succès (0 feu vert)
Il existe trois modalités pour avoir un seul succès (1 feu vert).
Il existe trois modalités pour avoir deux succès (2 feus verts)
Il existe une seule modalité pour avoir 3 succès (3 feus verts).
Plutôt que de connaître la probabilité de chacune de ces modalités (qui sont données par l’arbre ci-dessus) ce qui nous intéresse est de connaître les probabilités de 0 ou 1 ou 2 ou 3 succès. Et ceci sans faire appel à un arbre qui est pratique pour de petites répétitions de l’épreuve ( ici 3), mais qui deviendraient fastidieuses pour des répétitions de l’épreuve plus importante( à partir de 4). Imaginons que nous ayons 10 feus rouges.
On détermine une variable aléatoire X qui prend pour valeur le nombre de succès obtenus. (0,1,2,3 dans notre exemple).
Cette variable aléatoire a pour loi de probabilité :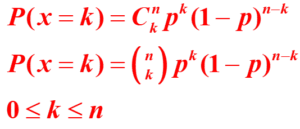
k est la valeur que prend successivement la variable aléatoire X .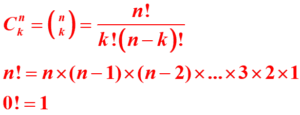
X suit une loi binomiale de paramètres n et p ![]()
Ainsi les coefficients 1,3,3,1 correspondent au nombre de combinaisons de k objets parmi n objets, dans ce cas au nombre de feus verts traversés parmi les trois feus verts.
Ce nombre de combinaison est donné par la formule :![]()
sachant que![]() et que 0!=1
et que 0!=1
Il existe deux écritures différentes pour nommer les combinaisons :![]()

Ce qui nous intéresse finalement ce n’est pas de connaître la probabilité d’avoir un feu vert, puis un rouge, puis un autre rouge ou bien celle d’avoir un feu rouge, puis un vert, puis un rouge, ou bien encore la probabilité d’avoir une feu rouge, puis un rouge, puis une vert. Ce qui nous intéresse c’est de connaître la probabilité d’avoir un seul feu vert. Cela revient à regrouper les trois probabilités précédentes en une seule.
C’est ce que nous allons faire avec la loi binomiale. ci dessous.
Si X est la variable aléatoire donnant le nombre de feus verts rencontrés, nous pouvons écrire les probabilités de chaque éventualité.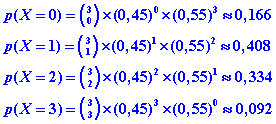
On vérifie que la somme de ces quatre probabilités est égale à 1.
Nous pouvons donc définir une formule donnant les différentes probabilités selon les valeurs d’une variable aléatoire. Voir ci-contre.
Loi binomiale
Résumons : 
Nous venons de voir que nous sommes intéressés par le nombre de feus verts que notre voiture va passer sans s’arrêter. Ce nombre de feus verts à passer est de 0 ou 1 ou 2 ou 3.
Désignons par X ce nombre.
Pour désigner la probabilité pour que 0 feu soit vert nous écrirons p(X=0)
Pour désigner la probabilité qu’un feu soit vert nous écrirons p(X=1)
Ainsi de suite avec p(X=2) et p(X=3).
X est appelée variable aléatoire.
Si X est la variable aléatoire donnant le nombre de feus verts rencontrés, nous pouvons écrire les probabilités de chaque éventualité.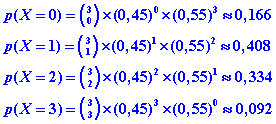
On vérifie que la somme de ces quatre probabilités est égale à 1.
Nous pouvons donc définir une formule donnant les différentes probabilités selon les valeurs d’une variable aléatoire. Voir ci-contre.
Propriété
Les propriétés de la loi binomiale sont les suivantes :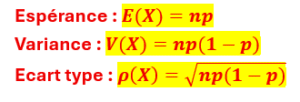
Démonstrations :
La loi Binomiale consiste à appliquer n fois le schéma de Bernoulli.
Donc l’espérance de la loi binomiale sera égale à n fois l’espérance du schéma de Bernoulli Il en est de même pour la variance.
Pour notre exemple de 3 épreuves (3 feus tricolores) sachant que la réussite d’une épreuve consiste à ce que le feu tricolore soit vert et que la probabilité de cette réussite est de 0.45, nous obtenons les résultats suivants 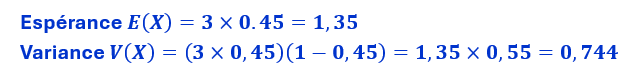
Cela signifierai que l’on pourrait s’attendre à un peu plus de un succès en moyenne, avec une dispersion de 0,744 autour de ce succès moyen. On pourrait donc tabler sur des succès étant dans une fourchette :
(1,35-0,744; 1,35+0,744)=(0,606; 2,94).
Mais notre résultat n’est pas significatif. En effet, il faudrait un plus grand nombre d’épreuves ( un plus grand nombre de feus tricolores.
Graphique
Avec les curseur n et p choisir respectivement le nombre de répétions et la probabilité de réussite
L’histogramme de la loi apparaît ainsi que sur la gauche toutes les valeurs prises par la variable aléatoire X.
Pour connaître la probabilité d’une variable aléatoire soit on, regarde dans le tableau, soit on règle le curseur k sur la valeur de la variable aléatoire. La probabilité se trouve à côté du curseur.
En haut à droite sont indiqués les paramètres de la loi choisie.
On lance 20 fois une pièce de monnaie et on regarde si elle est tombe sur pile.
Comme on reproduit 20 fois le lancé, n=20. Comme il n’ existe que deux éventualités, on a une chance sur 2 de tomber sur un pile. p=0,5
Lorem ipsum dolor sit amet, consectetur adipiscing elit. Ut elit tellus, luctus nec ullamcorper mattis, pulvinar dapibus leo.