Formules trigonométriques
- par gabriel
- dans Articles nouveaux, Mathématiques, Trigonométrie
- sur 4 mai 2024
Rappel
Le cercle trigonométrique à pour centre O de coordonnées (0,0) et pour rayon AO=1.
Le point M est un point du cercle. il génère un angle ![]() dont la valeur en radians est égale à θ.
dont la valeur en radians est égale à θ.
Si θ est positif l’angle ![]() apparaît en rouge. Pour aller de A à M on tourne dans le sens inverse des aiguilles d’une montre. C’est le sens trigonométrique, habituellement utilisé en mathématiques.
apparaît en rouge. Pour aller de A à M on tourne dans le sens inverse des aiguilles d’une montre. C’est le sens trigonométrique, habituellement utilisé en mathématiques.
Si θ est négatif l’angle ![]() apparaît en bleu. Pour aller de A à M on tourne dans le sens des aiguilles d’une montre, c’est le sens négatif en trigonométrie.
apparaît en bleu. Pour aller de A à M on tourne dans le sens des aiguilles d’une montre, c’est le sens négatif en trigonométrie.
Pour faire varier la valeur de l’angle on utilise le curseur vert θ en maintenant appuyer le bouton gauche de la souris tout en la glissant à droite ou à gauche.
On peut introduire la valeur d’un angle dans la case texte en vert « Angle θ ».
On peut introduire cette valeur soit en radian comme sur le curseur, soit en fraction de pi (on introduit le terme « pi ») : ex 2pi/3, pi/2…..La mesure est en radian, soit encore en degrés en faisant suivre le nombre du symbole des degrés °. ex 60°.
On obtient les valeurs des cosinus, sinus et tangente . Ce sont des valeurs approchées avec deux décimales.
Valeurs particulières

.
Formules indispensables

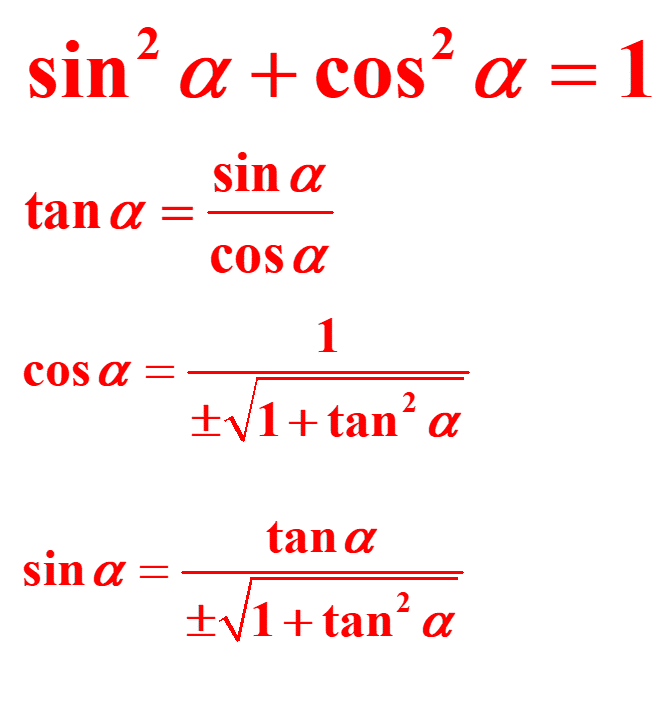





Ces formules doivent être connues par cŒur
Angles opposés, supplémentaires, complémentaires.








On peut facilement retrouver ces formules grâce au cercle trigonométrique. Inutile de charger sa mémoire.
Formules d'addition

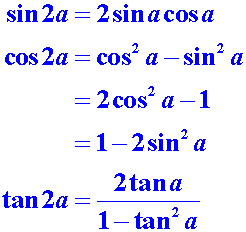




Lorsque j’étais en terminale section mathématiques élémentaires, on devait connaître toutes ces formules.