Probabilités : généralités
Espaces probabilisés finis
Parties d'un ensemble
Dans un ensemble E on peut regrouper ses éléments de différentes façons. On peut même envisager tous les regroupements possibles. Un regroupement est appelé Partie de l’ensemble et est noté : 
Le cardinal de l’ensemble des parties de E, c’est à dire le nombre de parties possibles dans un ensemble E constitué de n éléments est donné par la formule :
Dans un ensemble E de n éléments on peut distinguer les parties à 1 éléments, les parties à 2 éléments,………., les parties à p éléments.
Le nombre de parties à p éléments dans un ensemble de n éléments est :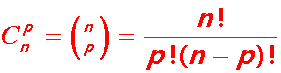
Rappel
la factorielle d’un nombre entier notée n! est le produit de tous les nombre entiers entre 1 et ce nombre. 
Par convention 0! est égale à 1
L’ensemble vide est une partie de l’ensemble E 
L’ensemble E lui même est une partie de l’ensemble. 
Toutes les parties d’un ensemble seront donc :
Albert, Brigitte, Charles, Didier et Elise, 5 anciens camarades de classe ont décidé de se rencontrer et de pratiquer des activités. Certaines activités sont individuelles, d’autres par couples, certaines en triplettes et enfin par quatre.
On désigne par E l’ensemble des camarades.
L’ensemble E a 5 éléments :
Le nombre total de parties de cet ensemble est :
Le nombre d’équipe sans personne est : 
Le nombre d’équipes à une personne est :
Le nombre d’équipes à deux personnes sera :
Le nombre d’équipes de trois personnes sera :
Le nombre d’équipes de quatre personnes sera :
Et enfin le nombre d’équipe à cinq personne sera :
Nous constatons que le nombre total de partie est biens égal à 32
Espace probabilisable fini, tribu
Très souvent on prendra :
Un espace E est probabilisable à certaines conditions.
E doit être un ensemble fini. C’est le cas de notre exemple :
Il y a un nombre fini d’éléments dans cet ensemble en l’occurrence 5.
Un sous ensemble B est une partie de l’ensemble P(E) des parties de E.
On prend une partie parmi toutes les parties de l’ensemble E.
On pourra inclure dans B parmi toutes les parties de l’ensemble des camarades, les parties ayant 2 personnes
On pourrait y inclure d’autres parties, les parties ayant 4 personnes :
Mais quoiqu’il en soit dans cet ensemble B on doit toujours y inclure l’ensemble E lui même
Dans cette configuration notre ensemble B sera
Si un sous ensemble A appartient à l’ensemble B, il faut que le sous ensemble complémentaire de A (ou contraires à A, non A), appartiennent à B
Si A est le sous ensemble des couples (deux personnes) avec Albert, l’ensemble des couples sans Albert doit appartenir à B. Ce qui est le cas.
Si est est un sous ensemble de B et C est un sous ensemble de B alors la réunion de A et de C est un sous ensemble de B
L’ensemble des trios avec Albert appartient à B.
L’ensemble des trios sans Albert appartient à B.
La réunion de ces deux ensembles, c’est-à-dire l’ensemble des trios appartient bien à B.
Le sous ensemble B ayant toutes ces propriétés est une tribu (sans e) sur E.
De plus
L’ensemble vide est élément de B
SI A et C sont éléments de B alors A∩C et A-C sont éléments de B.