FRACTIONS
On partage une tarte
Tout le monde a vu ou sait partager une tarte en plusieurs parts égales. On peut la partager facilement en 2, en 3, en 4.
C’est plus difficile de la partager en 5, en 7….
Pour la partager en 6, on la partage en 3 et on partage chaque part en 2.
Si vous êtes 6 enfants, la maman de Hugo partagera la tarte en 6 parts égales et tu en mangeras une part. C’est ce qui se passe dans la vie réelle.
Mais en mathématiques on a inventé une méthode qui permettra de traduire n’importe quelle situation de division, de partage.
Le fait de partager la tarte en 6 parts égales et d’en manger une se traduit par une fraction. 
En français on dira un sur six car le 1 est au dessus du 6.
On peut dire encore un sixième.
Le trait qui sépare le 1 et le 6 s’appelle la barre de fraction.
Le chiffre au dessous de la barre de fraction se nomme le dénominateur, il indique en combien de parts égales on a partagé la tarte.
Le chiffre au-dessus de la barre de fraction se nomme le numérateur, il indique le nombre de part que tu manges.
Sur l’animation ci-contre, tu peux voir le partage d’une tarte avec le nom donné à une partie.
Tu manges un certain nombre de parts
Finalement tu n’es pas obligé de na manger qu’une part de tarte, tu peux si ton estomac le permet en manger plusieurs.
Avec l’animation ci-contre :
Avec le curseur rouge,
tu choisis d’abord en combien de parties égales tu découperas ta tarte.
Avec le curseur bleu tu choisis le nombre de part que tu mangeras.
Fractions : et si on simplifiait
Une tarte partagée plus simplement
Fais glisser le curseur bleu vers la droite pour définir le nombre de parts que tu vas manger
sur les 12 parts ( tu peux même manger la tarte entière !!!)
Les règles de la simplification
Simplifier une fraction consiste à trouver une fraction dont le numérateur et le dénominateur sont plus petits que ceux de la fraction d’origine.
Pour cela on utilise la règle ci contre.
On a intérêt à trouver le plus grand nombre qui divisera à la fois le numérateur et le dénominateur d’une fraction. Ce plus grand nombre s’appelle le PGCD le plus grand commun diviseur ou plus grand diviseur commun.
Lorsqu’on ne peut plus simplifier la fraction, on dit qu’elle est irréductible. C’est la fraction la plus simple.
Pour simplifier une fraction on peut utiliser différents techniques.
– si on connaît bien les caractère de divisibilité, on peut trouver par quel nombre la fraction peut être simplifiée.
– Utiliser les décompositions en produit de facteur premier
– Utiliser le PGCD.
– Utiliser la calculatrice ou un logiciel (non recommandé !)
Simplifier mentalement
Première méthode : pour les fractions simples avec calcul mental
1- Peut-on simplifier la fraction par 2 ? Le numérateur et le dénominateur de cette fraction sont-ils tous les deux divisibles par 2 ? Si oui on simplifie et on passe à la deuxième étape, si non on essaie avec 3, 5, 7, …
2- Peut-on simplifier le résultat de la simplification précédente par 3 ? Les numérateurs et dénominateurs sont-ils divisibles par 3 ?
etc.
Il est nécessaire de bien connaître les caractères de divisibilité :
un nombre est divisible par 2 s’il est terminé par 0, 2, 4, 6 ,8 ( un nombre pair)
Un nombre est divisible par 3 si la somme de ses chiffres est un multiple de 3.
Un nombre est divisible par 4 si le nombre formé par ses deux derniers chiffres est un multiple de 4.
Un nombre set divisible par 5 s’il est terminé par 0 ou 5.
Un nombre est divisible par 9 si la somme de ses chiffres est un multiple de 9.
Un, nombre est divisible par 10 s’il est terminé par 0.
Pour la divisibilité par 7, il existe plusieurs méthodes compliquées, il vaut mieux essayer de faire la division.
Simplifier en décomposant en produit de facteurs premiers
Deuxième méthode :
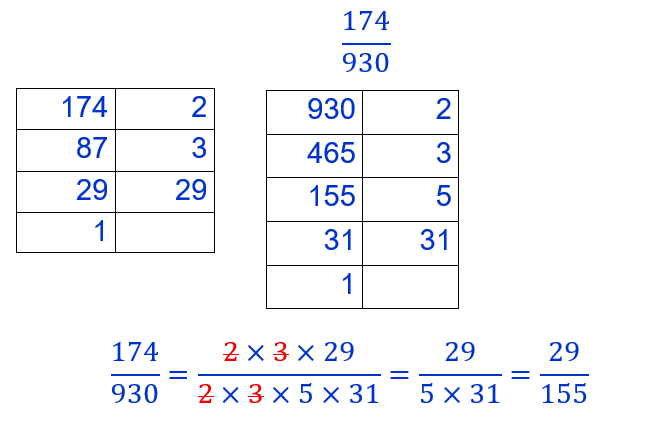
On décompose le numérateur et le dénominateur en produit de facteurs premiers.
On remplace dans la fraction le numérateur et le dénominateur par leur produit de facteurs.
On simplifie en barrant les facteurs communs au numérateur et au dénominateur.
Simplifier avec le PGCD
Troisième méthode :
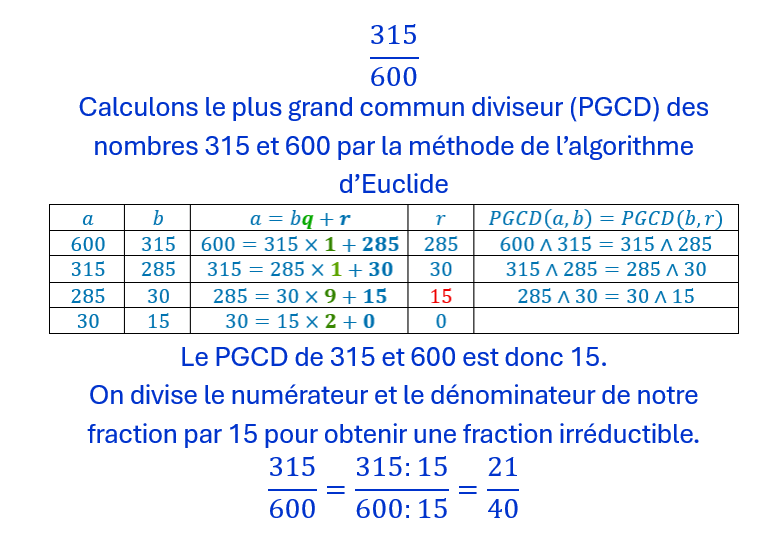
On calcule le PGCD du numérateur et du dénominateur.
On divise le numérateur et le dénominateur par le PGCD (4 méthodes pout cela) .
On obtient une fraction irréductible.
Addition de fractions
Faire glisser le curseur jusqu’à 1, observer les changements et lire les encadrements.
Puis faire glisser le curseur jusqu’à 2 puis 3 jusqu’à 5.
Si tu as deux tartes de même dimension , la première est partagée en neuf et la seconde en trois.
Avec la première tarte chacune des parts est un neuvième de la tarte.
Avec la seconde chacune des parts est un tiers de la tarte.
Tu as appris déjà, je pense qu’on ne pouvait pas additionner des torchons et des serviettes, des chiens avec des chats.
Là aussi comme tes parts ne sont pas égales, tu ne peux pas les additionner.
Tu ne peux pas additionner des neuvièmes avec des tiers.
Tu ne peux additionner que des neuvièmes ensemble ou des tiers ensemble, mais pas les deux.
Pour pouvoir additionner des fractions, elles doivent avoir le même dénominateur.
Lorsque les fractions ont le même dénominateur, on additionne leur numérateur pour obtenir la somme des deux fractions..
Si tu manges deux neuvièmes de la première tarte et un tiers de la seconde, tu aurais mangé trois quoi ? (trois neuvièmes, trois tiers ? )
Mais si tu manges deux neuvièmes de la première et trois neuvièmes de la seconde, tu as bien mangé cinq neuvièmes de tarte.
Pour additionner deux, ou plusieurs fractions, on doit les réduire au même dénominateur.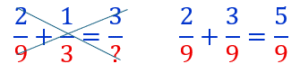 
Réduire au même dénominateur
Dans notre exemple ci-dessus, pour avoir le même dénominateur aux deux fractions, on peut multiplier le numérateur et le dénominateur de la seconde fraction par 3.
Mais si nous avions six neuvièmes plus un tiers , il suffirait de diviser le numérateur et le dénominateur de la première fraction par 3.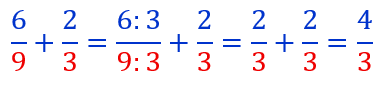
Réduire au même dénominateur : Méthode standard
C’est la première méthode qu’on apprend à l’école.
Soit l’addition de deux fractions suivante :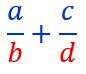
On prend comme dénominateur commun le produit des deux dénominateurs b x d (bd).
Comme dans la première fraction, on a multiplié son dénominateur par d, pour ne pas changer la valeur de cette fraction il nous faut multiplier aussi son numérateur par d.
Comme dans la seconde fraction, on a multiplié son dénominateur par b, pour ne pas changer sa valeur, il nous faut aussi multiplier son numérateur par b .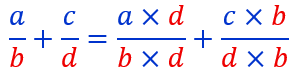
Qu’on peut écrire en respectant l’ordre alphabétique et en supprimant le signe X :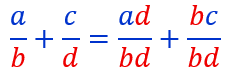
Le résultat sera :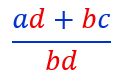 
Soit l’addition suivante de deux fractions :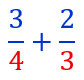
On prend pour dénominateur commun le produit des deux dénominateurs : 
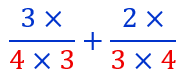Comme on a multiplié le dénominateur de la première fraction par 3, il nous faut aussi multiplier son numérateur par 3.
De même comme on a multiplié le dénominateur de la seconde fraction par 4, il nous faut aussi multiplier son numérateur par 4.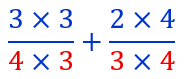
Il ne reste plus qu’à effectuer les opérations :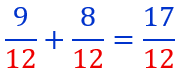
Réduire au même dénominateur : calcul du PPCM
Qu’est-ce que le PPCM ?
le plus petit commun multiple.
Pour trouver les multiples d’un nombre, il suffit de multiplier ce nombre par tous les entiers naturels.
Les multiples de 8 sont 8 x1, 8 x 2, 8 x 3, etc
8, 16, 24, 32, 40, 48, 56, 64, 72, 80, 88, 96 … il y en a une infinité
Les multiples de 6 seront
6, 12, 18, 24, 30, 36, 42, 48, 54, 60, 66, 72, 78, 84, 90, 96, ….
Les multiples communs à 8 et à 6 sont donc :
24, 48, 72, 96 …
Et le plus petit de ces multiples communs est bien évidemment 24.
On a donc intérêt à prendre 24 comme dénominateur commun pour les deux fractions ci-contre.
En prenant 24 on multiplie le numérateur et le dénominateur de la première fraction par 3 et le numérateur et le dénominateur de la seconde fraction par 4.
Voyons cet exemple avec la méthode précédente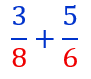 
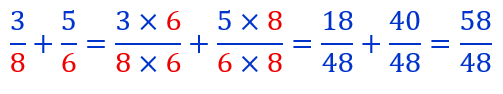
On voit que l’on peut simplifier le résultat par 2.
En prenant pour dénominateur commun le plus petit multiple commun à 8 et 6, on aurait trouvé directement le résultat avec une fraction irréductible. Ce plus petit multiple commun (PPCM) est 24. Voir ci-contre comment le trouver. 