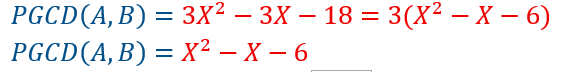Les polynômes
Monôme
Un monôme est une expression mathématique constituée d’un seul terme :
une constante, une variable, un produit de constantes et de variables avec des exposants entiers naturels.
On peut additionner ou soustraire des monômes à condition que leur partie littérale soit identique.
sont des monômes
Remarques
A l’intérieur des monômes, on ne rencontre pas d’addition ou de soustraction, mais seulement des multiplications.
Pour pouvoir s’y retrouver facilement, les éléments sont rangés : d’abord les nombres, ensuite les lettres par ordre alphabétique munis d’exposants ou non.
On peut additionner ou soustraire :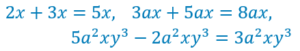
on peut dire qu’ils ont le même nom.
On ne peut pas additionner ou soustraire 
On peut dire qu’ils n’ont pas le même nom.
Pour alléger l’écriture : 
Polynômes : définition
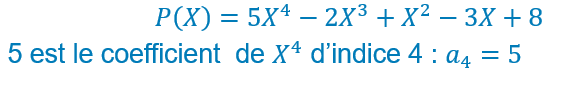
A la place de X
Avec des coefficients appartenant à l’ensemble des nombres rationnels :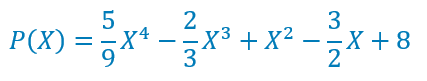
Avec des coefficients appartenant à l’ensemble des réels :
Avec des coefficients appartenant à l’ensemble des nombres complexes :
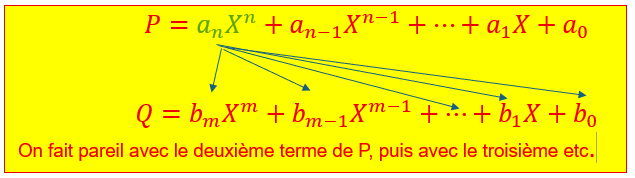
Deux manières d'écrire les polynômes
En général, on écrit les polynômes comme il est indiqué dans la définition, c’est à dire suivant les puissances décroissantes de X.
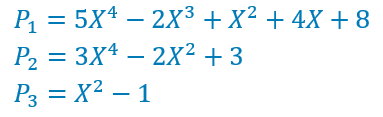
On peut aussi les écrire pour ainsi dire à l’envers, suivant les puissances croissantes de X.
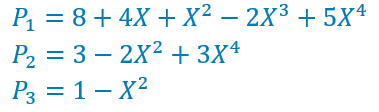
Polynômes : opérations
Egalité de deux polynômes
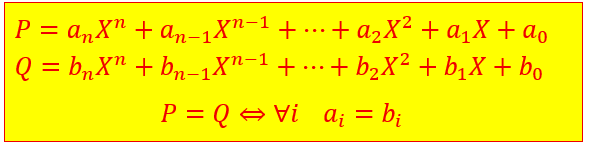
Ces deux polynôme sont bien évidemment égaux.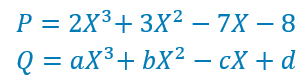 
Pour que Q soit égal à P il faut et il suffit que 
Addition de deux polynômes
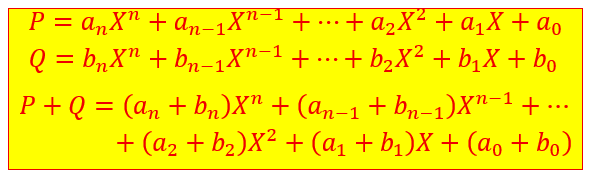
Pour bien montrer qu’on additionne chaque coefficient ayant le même indice, on a décalé l’expression de Q afin que les X ayant même exposant soient les uns sous les autres. Cela facilite aussi les calculs. Il est évident que le coefficient de X puissance 4 du polynôme Q est égal à 0.
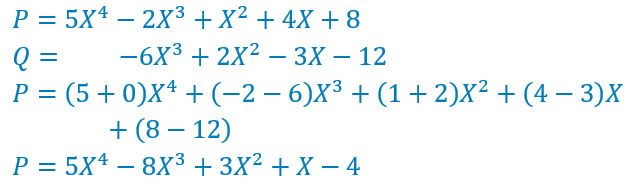
La démarche est identique avec plus de deux polynômes.
Propriétés de l'addition des polynômes
L’addition des polynôme est commutative.
L’addition des polynôme admet un élément neutre noté 0.
L’addition des polynômes est associative.
Le degré du polynôme somme P+Q de deux polynôme P et Q est inférieur ou égal au degré maximum des deux polynômes P et Q.
est l’ensemble des polynôme dont le degré est inférieur ou égal à n.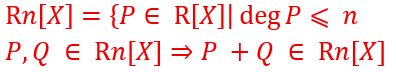 
Si deux polynômes P et Q appartiennent à l’ensemble des polynômes dont le degré est inférieur ou égal à n, la somme de ces deux polynômes P+Q appartient aussi à cet ensemble.
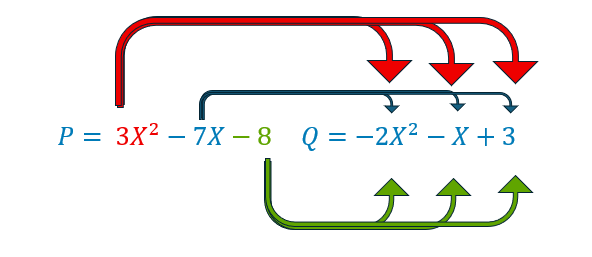
Multiplication de deux polynômes
C’est une définition bien compliquée difficile à décortiquer complètement. 
Pour multiplier plusieurs polynômes, on multiplie les deux premiers entre eux, puis on multiplie le résultat par le troisième polynôme et ainsi de suite.
Cela s’appelle un développement.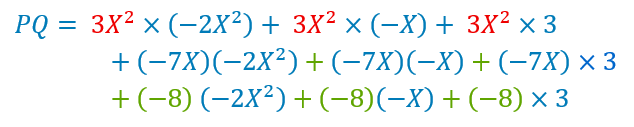 
On n’écrit pas cette ligne en générale, on passe directement à la ligne du dessous en calculant mentalement.
Conseil : on s’occupe tout d’abord du signe du résultat qu’on écrit immédiatement. pour 3X² multiplié par -2X² le signe est négatif et ensuite on procède à la multiplication
On vient d’effectuer la multiplication de manière horizontale. On peut l’effectuer de manière verticale comme la multiplication de deux nombres.
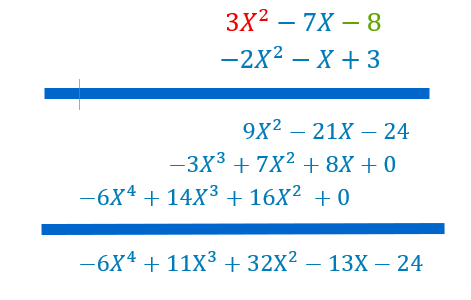
Propriétés de la multiplication des polynômes
La multiplication des polynôme est commutative.
.
La multiplication des polynômes admet un élément neutre noté 1.
La multiplication des polynômes est associative.
La multiplication des polynômes est distributive par rapport à la somme.
Le degré du produit PQ de deux polynômes P et Q est égal à la somme des degrés de chacun des deux polynômes.
Multiplication par un scalaire
.
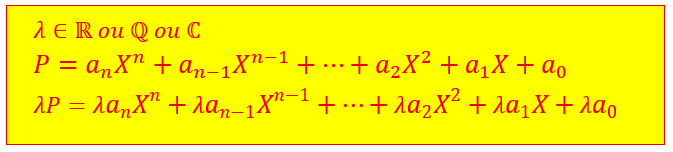
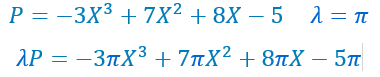
Division de deux polynôme
La division euclidienne de deux polynômes et la division euclidienne de deux nombres réels se ressemblent sur de nombreux points.
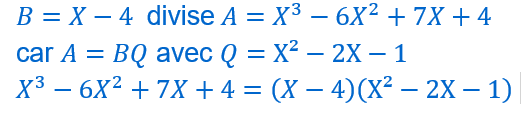
On peut vérifier en multipliant les deux polynômes B et Q du second membre pour retrouver le polynôme A du premier membre.
.
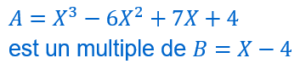
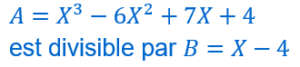
Propriétés de la relation divise
.
Deux polynômes qui se divisent mutuellement ne peuvent être que des multiples non nuls l’un de l’autre.
Ils ont exactement les mêmes racines avec les mêmes multiplicités, seule la constante multiplicative change.
Soient deux polynômes A et B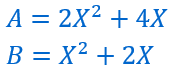
Si on factorise A par 2 :
on remarque que A divise B et que B divise A et que A=2B
La relation divise est transitive.
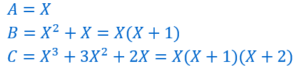
En prenant les formes factorisées de chaque polynôme il est évident que
A divise B, que B divise C et que A divise C
C divise A et C divise B signifie que A et B possèdent le même facteur C.
Si on multiplie A par un polynôme U quelconque et B par un autre polynôme V quelconque et que l’on fait la somme AU+BV des deux résultats, cette somme possèdera le même facteur C
L’opération AU+BV est une combinaison linéaire de A et de B.
C’est la même chose avec des nombres.
6 divise 12 et 6 divise 18
On peut choisir deux nombres quelconques, par exemple 5 et 7.
6 divise (12×5)+(18×7)
6 divise 60+126
6 divise 186
186/6=31
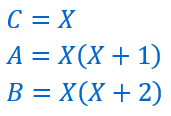
On remarque que c divise A et que C divise B.
Choisissons deux polynômes U et V , n’importe lesquels.
Calculons AU puis BV.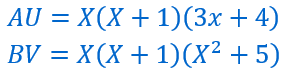
Effectuons la somme :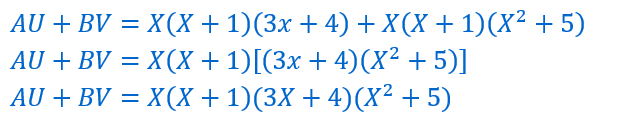
Nous voyons que C divise AU+BV.
Division euclidienne des polynômes.
Lorsque les polynômes A et B ne sont pas divisibles l’un l’autre, on peut néanmoins diviser A par B. L’opération se nomme division euclidienne :
On place le polynôme dividende A et le dividende diviseur B comme pour la division de deux nombres.
Ensuite on procède comme indiqué dans l’animation ci-dessous.
Pour le dividende A si les puissances de X ne se suivent pas, on a intérêt à laisser la place à celles qui manquent.
On peut diviser deux polynôme écrits tous les deux suivant les puissances croissantes de X . Le processus est le même.
Ainsi nous pouvons écrire :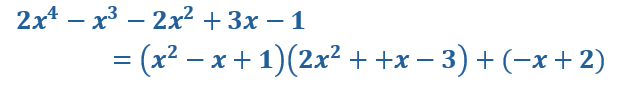 
Exemple où il manque une puissance de X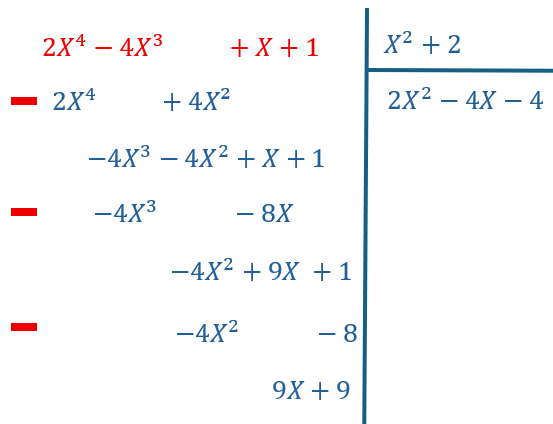 
Exemple de division de deux polyn^mes écrits selon les puissances croissantes de X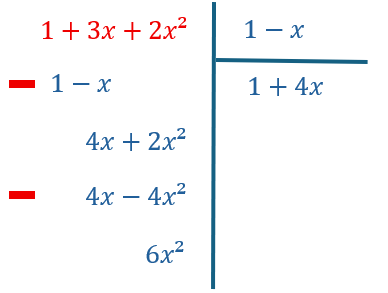 
Attention : cette division n’est pas une division euclidienne.
Racines des polynômes, factorisation
On peut penser que P(X) le polynôme et p(x) la fonction, c’est la même chose. Il y a cependant une nuance subtile.
Si un nombre a annule la fonction, elle annule aussi le polynôme.
Comme on peut factoriser la fonction par (x-a) on peut factoriser le polynôme par le polynôme (X-a).
On a différencier les X du polynôme et les x de la fonction pour bien comprendre mais ce n’est pas nécessaire.
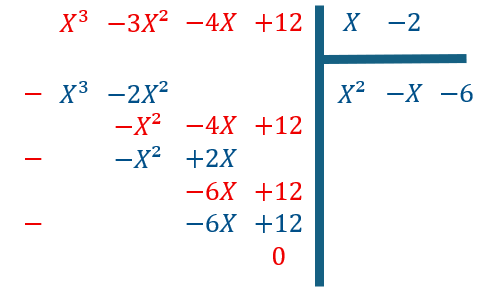
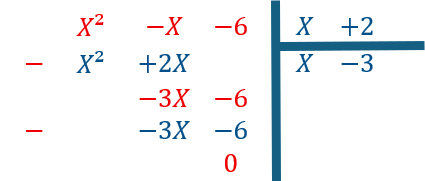
Soit le polynôme : 
On lui associe la fonction :
Essayons de trouver un nombre qui annule cette fonction, donc le polynôme. On peut essayer parmi les nombres : 
On s’aperçoit que le nombre 2 annule la fonction.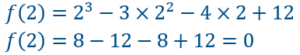 
2 annule aussi le polynôme qui peut être factorisé par X-2 comme la fonction par (x-2).
Il reste à trouver (……..).
Deux méthodes pour cela :
Par identification.
Comme F(X) est un polynôme du troisième degré qu’on divise par un polynôme du premier degré, le résultat (……..) sera obligatoirement un polynôme du deuxième degré qu’on peut écrire ax²+bx+c.
On remplace le premier membre par sa valeur. On développe le second membre :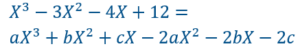
Toujours dans le second membre on ordonne selon les puissances décroissantes de X.
On factorise dans le second membre par X² et X .
On identifie les coefficients :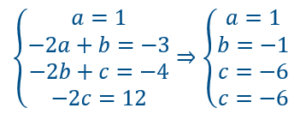
On peut donc écrire :
En effectuant la division des polynômes : voir ci contre.
On procède de la même façon avec le polynôme X²-X-6.
On remarque que -2 est une racine de ce polynôme
(-2)²-(-2)-6=0
et qu’il peut être factorisé par X-(-2) soit X+2
Par identification on trouve a=1 et b=-3.
Voir la division de ce polynôme ci contre
Le polynôme X3-3X²-4X+12 a complètement été factorisé. 
Cela signifie que ce polynôme est divisible par (X-2), par (X+2), par (X-3), mais pas que
Diviseurs d'un polynôme
Soit le polynôme : 
Nous avons vu précédemment qu’il pouvait être factorisé :
Ce qui signifie que (x-2) est un diviseur de A, ainsi que (x+2) et (x-3).
Mais aussi ( x-2)(x+2).
On peut trouver tous les diviseurs de A.
Les diviseurs de A sont toutes les combinaisons possibles des facteurs de ce polynôme. 
Soit le polynôme :
Nous savons que nous pouvons factoriser ce polynôme en procédant comme pour le polynôme A . Nous e détaillerons pas les calculs. La factorisation de B est la suivante : 
Et on trouve tous les diviseurs de B :
PGCD de deux polynômes
Pour trouver le PGCD de deux polynômes, une méthode consiste à :
1- chercher toutes les racines de chaque polynôme.
2- les factoriser à partir des racines en polynômes irréductibles.
3- noter tous les diviseurs de chaque polynôme en effectuant toutes les combinaisons des facteurs de chacun.
4-ordonner ces diviseurs suivant leur puissance croissante.
5- faire la liste des diviseurs communs.
6- celui qui a la puissance la plus élevée est le PGCD En général c’est le dernier de la liste.
Cette méthode est longue et fastidieuse. Une méthode est beaucoup plus simple en appliquant l’algorithme d’Euclide.
Pour les deux polynômes du paragraphe précédent :
on a trouvé tous les diviseurs de chacun d’eux.
On remarque dans leur tableau qu’ils ont des diviseurs en commun. 
et le plus grand est x²-x-6.
Retenons la dernière assertion. 
Elle permet de calculer le PGCD avec l’algorithme d’Euclide.
On procède à la division euclidienne de A et B
On obtient un quotient Q et un reste R
Le PGCD de A et B est égal au PGCD de B et R
On procède à la division euclidienne de B et de R
…… ainsi de proche en proche on obtiendra en fin du processus le PGCD.
Voir le tableau ci-dessous :
Soient 2 polynômes A et B 
On peut factoriser B :
Il est évident que A divise B et que A est différent de 0.
Nous en déduisons le PGCD des 2 polynômes :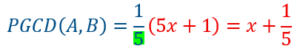 
Soient 2 polynômes A et B, A pouvant être factorisé par le nombre 3 :
Calculons les PGCD de (3A,B) et de (A,B) :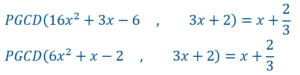
Ils sont identiques.
Algorithme d'Euclide
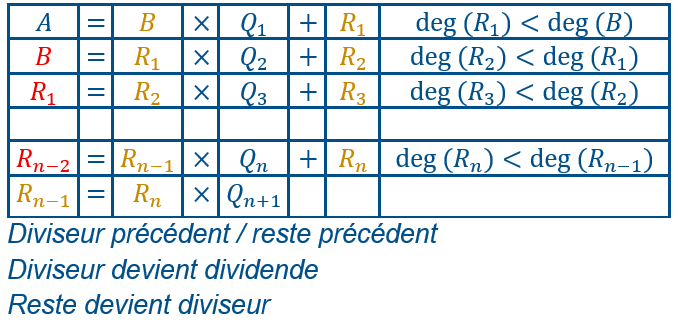
On divise A par B, on obtient un quotient Q1 et un reste R1
On divise B par R1, on obtient un quotient Q2 et un reste R2
On divise R1 par R2, on obtient un quotient Q3 et un reste R3
On divise R2 par R3, on obtient un quotient Q4 et un reste R4
On continue jusqu’à ce que le reste Rn soit égal à 0.
Alors le PGCD est égal à l’avant dernier reste Rn-1, celui qui est avant le reste 0.
C’est un peu compliqué, il ne faut pas se perdre dans les remplacements entre dividendes, diviseurs et restes. Remarquons que les quotients n’interviennent pas dans l’algorithme.
Soient deux polynômes A et B dont on veut calculer le PGCD.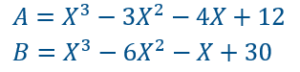 
On divise A=(X3-3X²-4X+12) par B= (X3-6X²-X+30), on obtient un quotient Q1=1 et un reste R1 =(3X²-3x-18).
On divise B=(X3-6X²-X+30) par R1=(3X²-3X-18), on obtient un quotient Q2= (1/3)X et un reste R2=-5X²+5X+30.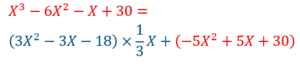
On divise R1=3X²-3X-18) par R2=(-5X²+5X+30, on obtient un quotient Q3=(-3/5) et un reste R3=0.
Le PGCD des polynômes A et B est donc 3X²-3X-18= 3((X²-X-6) = X²-X-6.
